7Определенный_интеграл

	где M 4 - максимальное значение абсолютной величины производной f IV (x) на отрезке [a,b] .
					2	dx
	Пример.5. Вычислить приближенно						.
					1	x
	2	dx		2
	Точное значение его		ln | x |		ln 2 . З точностью до седьмого знака ln 2			0,6931472.
		x		1
	1

Вычислим теперь его значение, пользуясь формулами (8.26-8.29). Для этого разделим отрезок
[1;2] на 10 равных отрезков. Тогда длина каждого из них будет x											2 1			0,1 .
										10
Составим табл. 2 значений подынтегральной функции в точках разбиения xi xi 1 0,1.
									Таблица 2
				1						1
		x		y x				x		y x
	x0	1,0	y0	1,00000			x6	1,6	y6	0,62500
	x1 1,1		y1 0,90909				x7	1,7	y7	0,58824
	x2	1,2	y2	0,83333			x8	1,8	y8	0,55556
	x3 1,3		y3	0,76923			x9	1,9	y9	0,52632
	x4	1,4	y4	0,71429			x	2,0	y	0,50000
							10		10
	x5	1,5	y5	0,66667

Тогда по формуле (8.26) получим																			2		dx	0,1( y			y		... y						) 0,1 7,18773 0,71877 .
																								0								9
																					x					1
																			1
По формуле (8.27)	2	dx		0,1( y							y				... y ) 0,1 6,68773 0,66877.
													2
	x					1															10
	1
	2		dx				1 0,5
По формуле (8.28)						0,1											6,18773 0,69377 .
			x								2
	1
По формуле Симпсона (8.29)
						2		dx						0,1				( y			y		2( y			y			y		y				)
																				0					2			4		6				8
										x					3						10
						1
					4( y1 y3 y5 y7 y9 ))
							0,1			(1 0,5 2 2,72818 4 3,45955 ) 0,69315 .
							3

Таким образом, по формуле Симпсона при n 10 получили 5 верных знаков, по формуле трапеций - лишь три верных знака, за формулами прямоугольников мы можем быть уверены только в одном знаке.

8. Применение определенного интеграла

Вычисление площадей плоских фигур

			f (x)	Площадь криволинейной трапеции,
				ограниченной линиями:	y f (x) , y 0 ,
				x a , x b. f (x) 0	при x [a;b].
		S		b
				S f (x) dx.
				a
a	0	b	x
y (x)			y (x)	Площадь фигуры, ограниченной линиями:
				y (x) , y (x) . (x) (x) на [a;b] .
				(Пределы интегрирования a и b являются
				решением уравнения (x) (x) ).

						b
					S ( (x) (x)) dx.
	a		b			a
		0	x
					Площадь сектора, ограниченного кривой,
		S			заданно в полярной системе координат
					( ) .
			( )		Сектор ограниченный кривой ( ) и
					лучами 1 та 2 .
	2					1	2
					S		2 d .
		1				2
					1

0

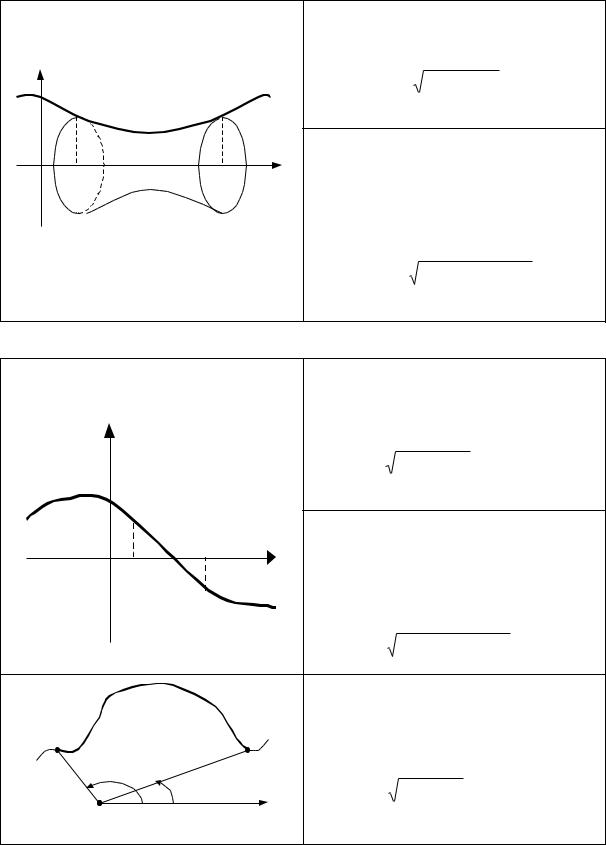
Объём тела вращения

Объѐм тела, образованного вращением вокруг оси Ох криволинейной трапеции aABb, где AB - дуга кривой y f (x) от

x a до x b.

b

V ( f (x))2 dx.

a

Площадь поверхности вращения

Площадь поверхности, образованной

вращением вокруг оси Ох участка кривой

y f (x) от x a до x b .

y

b

y=f(x)

2 f (x)

1 ( f

2

dx.

(x))

A

B

a

Площадь поверхности вращения,

образованной вращением вокруг оси Ох

0

a

b

x

участка кривой, заданной в

параметрическом виде:

x x(t),

t1 t t2

:

y y(t).

t2

2 y(t)

2

2

dx.

(x (t))

( y (t))

t1

Длина дуги плоской кривой

Если кривая задана в прямоугольной

декартовой системе координат

уравнением y f (x) , от точки (a, f (a))

y

до (b, f (b)), то

b

S AB

1

2

dx.

y f (x)

( f (x))

a

A

Если кривая задана параметрически:

b

x x(t),

то точки А та В имеют

0

a

x

y y(t),

координаты

A(x(t1 ); y(t1 )),

B

B(x(t2 ); y(t2 )), то

t2

S AB

2

2

dt.

(x (t))

( y (t))

t1

Если кривая задана своим уравнением

в полярных координатах: ( ) и

B

A

координаты точек А и В:

A( 1; ( 1 )),

B( 2 ; ( 2 )),

то

2

2

1

2

LAB

2

d .

( )

0

1

Примеры:

																												1				5					e	dx			5
																																										e 4 x dx.
			Пример 1. Вычислить интегралы: а)																										9x						1 dx;	б)		x	;	в)
																												0					x				1				0
																													Решение:
	1								5							9				2							1
а)				9x									1 dx				x						10 x x |
										x					2												0
	0
				9			2									9						2								9
							1			10 1 1										0			10 0 0								;
				2												2														2
	e		dx							e
б)						ln x |							ln e ln1 1							0			1;
				x
	1								1

			0						1		0	1	e 4 0 e 4 ( 5 )						1	e0 e20						e	20	1
в)			e 4x dx							e 4x |																				.
			5						4		5	4							4								4
																								dx
			Пример 2.						Исследовать на сходимость интеграл																.
																								2
																					1	1		x
																Решение:
			dx			b			dx					b														.
					lim						lim (arctgx) |				lim (arctgb arctg1)
			2						2
1	1		x		b	1	1		x		b			1		b								2 4 4
Т.о., данный интеграл является сходящимся.
			Пример 3.							Найти площадь фигуры, ограниченной параболой y (x 2)2																						и прямой y x.
																	Решение:
				Найдем точки пересечения прямой с параболой:
										y ( x 2 )			2 ,		x ( x 2 )2		,			x 2	5x 4 0,										x1 1,	x2 4;
																																y2 4.
											y x;					y x;								y 0;							y1 1,

Искомую площадь найдем как разность двух площадей криволинейных трапеций: ограниченных прямой и параболой.

									4					y								S	y=(x-2)2						y=x
									1
									0				1					2					3			4			x
			4														4															x	3		5x	2	4
		S		(x (x 2)2 )dx														( x2					5x 4)dx														4x |
																															3			2
			1														1																				1
				4	3	5 4			2												1					5 1					9 .
											4 4																		4 1
																					3					2
				3		2															3					2					2
Ответ:	9	(кв.ед.).
	2

Пример 4. Найти площадь плоской фигуры, ограниченной кардиоидой																																																															a(1 cos ).
																																		Решение
																															2																1		2
																								S									2 ( )d																(a(1 cos ))2 d
																																															2
																															0																		0
																												1					2
																															a 2			(1 2 cos cos2 )2 d
																											2
																																	0
																												1			a 2		2																	1 cos2
	0												2a			p																		(1 2 cos																										)d
																											2						0																						2
																											1					2			2				3															1
																															a											2 cos													cos2 d
																											2						0						2															2
																											1					2	3																	1										2
																															a						2 sin																sin 2							|
																											2						2																	4										0
	1			2			3									1											3															5														3			2
			a							2 2sin 2									sin 4											0 2sin 0																	sin 0											a		.
	2						2									4								2																		4														2
Пример 5. Вычислить объѐм тела, образованного вращением вокруг оси Ох косинусоиды в
пределах от											до			.
									2				2
																																	Решение:
																																											b
Объем тела вращения находим по формуле																																					V ( f (x))2 dx,																					где в нашем случае
																																											a
f (x) cosx,									a ,					b	.
												2			2
											2		2							2		1 cos2x																				2
			V									cos		x dx																				dx								(1 cos2x)dx
																											2														2
											2										2																				2
																																																																2
												1		2										1																		1
										(x			sin 2x) |													sin																			sin( )																			.
							2					2							2		2 2																		2			2																2 2				2		2
														2

x a(t sin t),

Пример 6. Вычислить длину одной арки циклоиды

y a(1 cost),

t [0;2 ].

Решение:

Длина дуги плоской кривой, заданной параметрически вычисляется так:

l	(xt )2 ( yt )2 dt.
	Тогда

x

y

x(t), t [ ; ]. Найдем для нашего случая

y(t),

xt (a(t sin t)) a(1 cost), yt (a(1 cost)) a sin t.

2									2
l		(a(1 cost))2		(a sin t)2 dt								a 2 (1 2 cost cos2			t sin 2 t)dt
0								0
2				2								2
								t					t					t 2
a		2 2 cost dt a					2				dt a 2 sin
					2 2 sin									dt	4a	cos				|
0				0				2			0		2					2		0

	t	0
4a cos		|	4a(cos0 cos ) 4a(1 ( 1)) 8a.
	2	2

Пример 7. Вычислить с помощью формулы трапеций приближенное значение

1

dx

определенного интеграла

0

при n = 10 .

1 x

Решение

1

Подынтегральная функция

y

. Разобьем сегмент [0;1] на 10

1 x

частей, получим точки xi

и вычислим yi

y(xi ) . Составим таблицу.

Используя данные, взятые из таблицы, приближенно вычислим

1

dx

1 0

y

0

y

10

y1 y2

y9

1 x

10

2

интеграл: 0

0,1 6,938 0,6938 0,69.

	1	dx	0,69.
	Ответ:
		1 x
	0

i	xi	yi
0	0	1
1	0.1	0.909
2	0.2	0.833
3	0.3	0.769
4	0.4	0.714
5	0.5	0.667
6	0.6	0.625
7	0.7	0.588
8	0.8	0.555
9	0.9	0.526
10	1	0.5