Курсовая Работа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет Математики и Информационных технологий

Кафедра Информационной безопасности и теории управления

КУРСОВАЯ РАБОТА

Моделирование движения системы зубчатых колёс. ---------------------------------------------------------------------------------------------------- (название темы)

Фундаментальная математика и механика ---------------------------------------------------------------------------------------------------- (название и номер специальности)

Проект выполнил студент ____________ ________________ _____________________ группа подпись, дата Ф.И.О.

Научный руководитель _________________ _______________ _____________________ должность подпись, дата Ф.И.О.

УЛЬЯНОВСК 2013г.

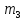Зубчатое колесо 2 массы и радиуса к находится во внутреннем зацеплении с зубчатым колесом 1 массы и радиуса R, вращающимся вокруг неподвижной горизонтальной оси О под действием постоянного момента Кривошип ОА массы в точке О насажен на ту же ось, а в точке А шарнирно соединен с центром колеса 2. К кривошипу приложен постоянный момент спиральной пружины жесткости с. При φ=0 пружина не деформирована.

1. Ввести подвижную систему координат, связанную с колесом 1. Считая θ(t) и φ(t) заданными функциями времени, вычислить абсолютную скорость и абсолютное ускорение точки А.

Скорость и ускорение точки А.

Обозначаем через ψ = (φ+θ) – угол поворота стержня ОА относительно оси (рис. 1), жёстко связанной с диском 1.

Принимая движение диска 1 за переносное, а поворот стержня ОА, определяемым углом ψ – за относительное движение, имеем:

(1)

где – переносная скорость точки А,

– относительная скорость точки А,

= абсолютная скорость точки А, направления векторов – на рисунке.

Проектируя уравнение (1) на ось (рис), получаем:

(2)

абсолютная скорость точки А.

Ускорение точки А:

(3)

Имеем:

Направления векторов показаны на рисунке.

Проектируя векторное уравнение (3) на оси ξ, η, получим:

(4)

• касательная и нормальная составляющая абсолютного ускорения точки А.

Угловые скорость и ускорение диска 2:

• угловая скорость диска 2

• .

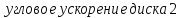2. Принять в этом пункте, что , колесо 2 не весомо, а в его центре A закреплена точечная масса . Считая θ(t) заданной функцией времени, составить векторное дифференциальное уравнение движения точки А относительно подвижной системы координат, введенной в пункте 1.

Здесь обозначено: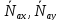 – составляющие реакции стержня ОА в точке А.

Дифференциальное уравнение относительного движения точки А:

Или в проекциях на оси ξ, η:

где

- силы инерции

Получаем:

Отсюда, после сокращений, получаем:

- система дифференциальных уравнений движения точки А.

3. Считая θ(t) и φ(t) заданными функциями времени, найти проекции реакции шарнира О. Применить теорему о движении центра масс. Показать, что

Определение реакций шарнира О.

Теорема о движении центра масс системы в проекциях на оси x,y:

где – суммарная масса системы, , – ускорения центра масс системы в проекциях на оси x, y,

- (10)

Координаты центра масс в осях x,y:

Дифференцируем (11) по времени t дважды:

Отсюда:

Подставляем (10), (12) в (9):

Отсюда:

- реакции в шарнире О.

4. Считая, что , составить дифференциальное уравнение движения системы, воспользовавшись теоремой об изменении кинетического момента системы относительно осей О и А.

Теорема об изменении кинетического момента:

Кинетический момент системы:

где – момент инерции однородного диска, – угловая скорость цилиндра, имеет противоположное направление по отношению к . – момент инерции стержня.

Получаем:

- кинетический момент системы.

Находим:

Сумма моментов внешних сил:

где – момент упругости пружины. – сила сцепления диска 2 с поверхностью качения.

Определяем силу сцепления, рассматривая равновесие диска 2 в соответствии с принципом Даламбера:

где , – угловое ускорение диска 2.

Получаем:

Подставляем в (16):

Приравниваем (16) и (18) в соответствии с (14):

Преобразуем:

- дифференциальное уравнение движения системы при .

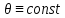5. Для условия пункта 4 определить, какую угловую скорость будет иметь стержень ОА в горизонтальном положении, если в верхнем вертикальном положении ему сообщена угловая скорость ω. Определить также, при каком условии стержень достигнет горизонтального положения. Применить теорему об изменении кинетической энергии системы.

Определение угловой скорости стержня ОА при достижении им горизонтального положения в условиях пункта 4.

Теорема об изменении кинетической энергии:

Находим:

где ,

Получаем:

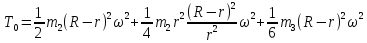
где - угловая скорость стержня ОА в конечный момент времени (при

Сумма работ внешних сил:

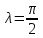где – угловая деформация пружины, так как в начальный момент пружина была не деформирована.

Получаем:

Подставляем (21),(22),(23) в (20):

Отсюда:

- искомая угловая скорость стержня ОА при .

6. Считая функции θ(t) и φ(t) заданными, определить главные векторы и главное моменты относительно центров масс сил инерции колес и стержня.

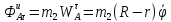
7. Используя принцип Даламбера, найти проекции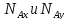 реакции шарнира А, а так же величину силы сцепления в точке касания колес 1 и 2. Показать что

В соответствии с принципом Даламбера механическая система под действием внешних сил и сил инерции находится в равновесии.

Составляем уравнения равновесия для диска 2, катящегося по внутренней поверхности диска 1:

Отсюда:

- реакция шарнира А.

Для определения силы составляем уравнение моментов относительно шарнира А для внешних и инерционных сил, действующих на диск 2:

Отсюда:

- сила сцепления.

8. Составить дифференциальные уравнения движения системы, исходя из общего уравнения аналитической динамики и приняв за обобщенные координаты θ и φ.

Общее уравнение динамики:

- сумма работ внешних сил и сил инерции на элементарных перемещениях системы равна 0.

1) Сумма работ на перемещениях

Отсюда, после сокращения на получаем:

- первое дифференциальное уравнение движения системы.

2) Сумма работ на перемещениях .

Сокращаем на: - второе дифференциальное уравнение движения системы.

9. Составить выражения для кинетической и потенциальной энергии системы, вычислить обобщенные силы.

Кинетическая энергия:

- кинетическая энергия системы.

Потенциальная энергия определяется работой потенциальных сил при возвращении системы в нулевое положение:

- потенциальная энергия системы.

Обобщенные силы:

Интеграл энергии системы:

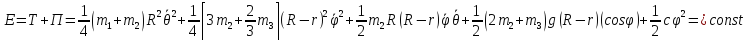
Циклические интегралы: Кинетический потенциал системы не зависят явно от координаты θ, т.е. θ – циклическая координата и соответствующий ей циклический интеграл имеет вид:

Или:

10. Используя уравнения Лагранжа второго рода, показать, что дифференциальные уравнения движения системы имеют вид Для случая записать интеграл энергии и циклический интеграл системы.

Уравнения Лагранжа второго рода: где - кинетическая энергия – (30), – обобщенные силы – (32), – обобщенные координаты.

Вычисляем производные от T:

Подставляем (32), (34) в (33):

Получаем: - дифференциальные уравнения движения системы совпадают с уравнениями (28), (29).

11. Полагая, что получить условие устойчивости верхнего положения относительного равновесия колеса 2. Найти период его малых колебаний в окрестности этого положения равновесия.

Малые колебания колеса 2 при . Первая производная от потенциальной энергии согласно (32) имеет вид:

Угол определяет положение равновесия системы, так как

Находим вторую производную:

Имеем: условие устойчивого равновесия при

Полагая в первом уравнении (35):

получаем дифференциальное уравнение колебаний диска 2 в окрестности устойчивого положения равновесия

или

где

- собственная частота системы.

Период малых колебаний:

12.Задавая численные значения параметров и начальные условия: составить программу решения системы дифференциальных уравнений и на ЭВМ построить зависимости .

Список литературы:

1) Задания для курсовых работ по динамике механических систем. М. Изд-во МАИ, 2005.

2)Руденко Т.В., Холостова О.В. Исследование движений голономных механических систем. М. Изд-во МАИ, 2005.

3)Маркеев А.П. Теоретическая механика: Учебное пособие. М.,Наука, 1990.

4)Бухгольц Н.Н. Основной курс теоретической механики: Учебник. М., Наука, 1965.

5)Золотых Н.Ю. Использование пакета MATLAB в научной и учебной работе. Изд-во ННГУ. Нижний Новгород, 2006г.

6)Лазарев Ю. Моделирование процессов и систем в MATLAB . Учебный курс. – СПб.: Питер; Киев: Издательская группа BHV. 2005.

7)Материалы образовательного математического сайта exponenta.ru

25