190-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-neskol-kih-peremennyh-1mb

Найдем значение функции в точке M3:

			z				3 2					, − 2 2						= −2						3 2						(−2 2 )− 5 = 12 − 5 = 7.
								2																				2
4. M			−		3			2								λ = −12.
	4										, 2			2 ,
								2
																						0						−						2					2
																															3								4
																= −				−			2						−				8						−2					=
																							3
																															3
																							2							−2								−			3
																						4
																																							2
					2						2					2				2								2			8						2							2		2		3			4
= − 2													+ 2										+																	+										= −		< 0.
					3 4									3 4														4 3 4																3 3 2							3

																							3 2
Следовательно,														в точке				M	4		−							, 2		2	функция имеет услов-
																								2
ный максимум.
Найдем значение функции в точке M4:
										3 2												3 2						(2 2 )− 5 = 12 − 5 = 7.
					z		−							, 2 2			= −2				−
										2														2
										3		2										−		3			2		, − 2
Итак,					M									, 2		2	,	M													2 – точки условного
						1						2								2				2
												= z				= −17 ;
минимума, z								M1							M2
		3			2						− 2							−	3		2
M	3						,							2 ,		M							, 2					2		–	точки условного макси-
					2												4				2
мума,		z		M3 = z							M 4 = 7 .

91

1.11. Наибольшее и наименьшее значение функции в замкнутой ограниченной области

Непрерывная функция u = f(x1, x2, …, xn), заданная на ограничен- ном и замкнутом множестве D, принимает на этом множестве наи- большее и наименьшее значения.

Наибольшее и наименьшее значения могут достигаться в стацио- нарных точках, лежащих внутри этой области или на ее границе.

Для нахождения наибольшего (наименьшего) значения функции в области D необходимо:

1)найти стационарные точки функции;

2)найти значение функции в стационарных точках, лежащих внутри области D;

3)исследовать функцию на границе области D;

4)сравнивая все значения, выбрать среди них набольшее (наи- меньшее).

Пример 1.11.1

Найти наибольшее и наименьшее значение функции z = 1 – 2x2 – y2 в области D: |x| + |y| ≤ 6.

Решение

Функция в замкнутой ограниченной области достигает своего наибольшего и наименьшего значения в стационарных точках, ле- жащих внутри области или на границе области.

Найдем стационарные точки функции, лежащие внутри области D:

	∂z	= −4x = 0,
	∂x
		M1(0,0).
	∂z
		= −2y = 0
	∂y

Точка M1 принадлежит области D, найдем значение функции в этой точке: z(0, 0) = 1.

Исследуем функцию на границе области D. Изобразим область D на координатной плоскости (рис. 1.4).

Запишем уравнения прямых AB, BC, CD и AD:

АВ: х + у = 6, 0 ≤ x ≤ 6;

BC: –x + y = 6, –6 ≤ x ≤ 0;

CD: –x – y = 6, –6 ≤ x ≤ 0;

AD: x – y = 6, 0 ≤ x ≤ 6.

92

Y
B	6
C		A
−6	O	6	X
D	−6

Рис. 1.4

На каждом из этих отрезков задача сводится к отысканию наиболь- шего и наименьшего значений функции одной переменной на отрезке.

1. Рассмотрим отрезок АВ. На данном отрезке y = 6 – x, где 0 ≤ x ≤ 6. Тогда

z = 1− 2x2 − (6 − x)2 = −2x2 − 36 + 12x − x2 + 1 = −3x2 + 12x − 35.

Найдем наибольшее и наименьшее значения функции z = −3x2 + + 12x − 35 на отрезке [0, 6].

Найдем стационарные точки:

z′ = −6x + 12 = 0; x = 2 [0, 6]; y = 6 − 2 = 4.

Тогда M2(2, 4) – стационарная точка, A(6, 0) и B(0, 6) – граничные точки.

Итак, M2(2, 4), A(6, 0) и B(0, 6) – точки, в которых функция может принимать наибольшее (наименьшее) значение. Найдем значения функции в этих точках:

z(2, 4) = 1 − 8 – 16 = −23; z(6, 0) = 1 –2 36 = –71; z(0, 6) = 1 – 36 = –35.

93

2.Рассмотрим отрезок BC. На данном отрезке у = 6 + х, где –6 ≤

≤x ≤ 0. Тогда

z = −2x2 − (6 + x)2 + 1 = −3x2 − 12x − 35.

Найдем наибольшее и наименьшее значения функции z = −3x2 −

– 12x − 35 на отрезке [−6, 0].

Найдем стационарные точки:

z′ = −6x − 12 = 0;

x= −2 [−6, 0]; y = 6 − 2 = 4.

Тогда M3(−2, 4) – стационарная точка, C(–6, 0) и B(0, 6) – гранич- ные точки.

Итак, M3(−2, 4), C(-6, 0) и B(0, 6) – точки, в которых функция мо- жет принимать наибольшее (наименьшее) значение. Найдем значе- ния функции в этих точках:

z(−2, 4) = −23; z(–6, 0) = –71; z(0, 6) = –35.

3. Рассмотрим отрезок CD. На данном отрезке у = −6 – х, где –6 ≤ x ≤ 0. Тогда

z = 1 − 2x2 − (−6 − x)2 + 1 = −3x2 − 12x − 35.

Найдем наибольшее и наименьшее значения функции z = −3x2 −

– 12x − 35 на отрезке [−6, 0].

Найдем стационарные точки:

z′ = −6x − 12 = 0; x = −2 [−6, 0]; y = −6 + 2 = −4.

Тогда M4(−2, −4) – стационарная точка, C(−6, 0) и D(0, −6) – гра- ничные точки.

Итак, M4(−2, −4), C(−6, 0) и D(0, −6) – точки, в которых функция может принимать наибольшее (наименьшее) значение. Найдем зна- чения функции в этих точках:

94

z(−2, −4) = −23; z(–6, 0) = –71; z(0, −6) = –35.

4. Рассмотрим отрезок АD. На данном отрезке y = x– 6 , где 0 ≤ x ≤ 6. Тогда

z = −2x2 − (x − 6)2 + 1 = −3x2 + 12x − 35.

Найдем наибольшее и наименьшее значения функции z = −3x2 + + 12x − 35 на отрезке [0, 6].

Найдем стационарные точки:

z′ = −6x + 12 = 0, x = 2 [0, 6], y = 2 − 6 = −4.

Тогда M5(2, −4) – стационарная точка, A(6, 0) и D(0, −6) – гранич- ные точки.

Итак, M5(2, −4), A(6, 0) и D(0, −6) – точки, в которых функция мо- жет принимать наибольшее (наименьшее) значение. Найдем значе- ния функции в этих точках:

z(2, −4) = −23, z(6, 0) = –71, z(0, −6) = –35.

Среди всех найденных значений выберем наибольшее и наименьшее:

max z(x, y) = z(0,0) = 1;

D

min z(x, y) = z(6,0) = z(−6,0) = −71.

D

Пример 1.11.2

Найти наибольшее и наименьшее значение функции z = 2x – 4y – 7 в области D: x2 + y2 ≤ 25, y ≥ x − 5.

Решение

Функция в замкнутой ограниченной области достигает своего наибольшего и наименьшего значения в стационарных точках внутри области или на границе области.

95

Найдем стационарные точки:

∂z = 2 ≠ 0;

∂x

∂z = −4 ≠ 0. ∂y

Следовательно, стационарных точек нет.

Исследуем функцию на границах области D. Изобразим область D на координатной плоскости (рис.1.5).

Y

M1

B

5 X

M2

A−5

Рис. 1.5

Разобьем границу области D на две части: часть окружности G1 и отрезок АВ – G2. Будем искать точки, в которых функция может принимать наибольшее и наименьшее значение на границах G1 и G2.

1. Рассмотрим часть окружности x2 + y2 = 25, лежащей в I, II и III четвертях.

Для нахождения наибольшего и наименьшего значения на грани- це G1 составим функцию Лагранжа:

L(x, y, λ) = 2х – 4у – 7 + λ(х2 + у2 – 25).

Найдем частные производные функции Лагранжа:

∂L = 2 + 2λx; ∂x

96

∂L = −4 + 2λy. ∂y

Координаты стационарных точек должны удовлетворять системе уравнений:

1

1

1

x

= −

,

x

= −

,

x = −

,

5

λ

λ

λ

2 + 2λx = 0,

λ = ±

,

5

2

2

2

−4

+ 2λy = 0, y

=

,

y

=

,

y =

,

x = 5,

λ

λ

λ

2

+ y

2

= 25

x

1

4

5

1

y = ±2 5.

+

= 25

= 25

λ 2

=

2

λ

2

2

5

λ

λ

Следовательно, M1(−

5, 2

5) и M2 (

5,

− 2

5) − стационарные

точки. Точка M2 ( 5,

− 2

5)

не принадлежит границе G1, следова-

тельно, находить значение функции в этой точке не надо.

Найдем значение функции в стационарной точке M1(−

5, 2

5) и

в граничных точках А(0, −5) и В(5, 0):

z(−

5, 2 5) = −2

5 − 8

5 − 7 = −10

5 − 7 ≈ −29,36;

z(5, 0) = 10 – 7 = 3;

z(0, –5) = – 4(–5) – 7 = 13.

2. Рассмотрим отрезок AB. На данном отрезке y = x – 5, где 0 ≤ x ≤ 5. Задача сводится к отысканию наибольшего и наименьшего значе-

ния функции одной переменной на отрезке [0, 5]:

z = 2x – 4(x – 5) – 7 = 2x – 4x + 20 – 7 = –2x + 13;

z′ = –2 ≠ 0.

Следовательно, стационарных точек на границе G2 нет; А(0, –5) и В(5, 0) – граничные точки. Значение функции в граничных точках А(0, –5) и В(3, 0) было найдено ранее.

Среди найденных значений выберем наибольшее и наименьшее:

min z(x, y) = z(− 5, 2 5) = −10 5 − 7 ≈ −29,36;

D

max z(x, y) = z(0, −5) = 13.

D

97

Пример 1.11.3

Найти наибольшее и наименьшее значение функции z = x2 + + 12xy + 2y2 в области D: 4x2 + y2 ≤ 25, y ≥ 0.

Решение

Функция в замкнутой ограниченной области достигает своего наибольшего и наименьшего значения в стационарных точках внутри области или на границе области.

Найдем стационарные точки:

∂z = 2x + 12y = 0;

∂x

∂z = 12x + 4y = 0.

∂y

Решим систему уравнений:

2x + 12y = 0,		x = −6y,	x = 0,
12x + 4y = 0	−72y + 4y = 0		y = 0.

Следовательно, M1(0, 0) − стационарная точка. Точка M1 принад- лежит области D, найдем значение функции в этой точке: z(0, 0) = 0.

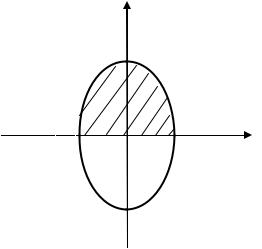
Исследуем функцию на границах области D. Изобразим область D на координатной плоскости (рис.1.6).

Y

5

A	B
	5/2	X

Рис. 1.6

98

Разобьем границу области D на две части: часть эллипса G1, рас- положенного выше оси OX, и отрезок АВ обозначим G2. Будем искать точки, в которых функция может принимать наибольшее и наимень- шее значение на граница G1 и G2.

1. Рассмотрим часть эллипса 4x2 + y2 = 25, лежащего в I и II чет- вертях.

Для нахождения наибольшего и наименьшего значения на грани- це G1 составим функцию Лагранжа:

L(x, y, λ) = x2 + 12xy + 2y2 + λ(4х2 + у2 – 25).

Найдем частные производные функции Лагранжа:

∂L = 2x + 12y + 8λx;

∂x

∂L = 12x + 4y + 2λy.

∂y

Координаты стационарных точек должны удовлетворять системе уравнений

2x + 12y

+ 8λx = 0,

x + 6y + 4λx = 0,

+ 4y

+ λy = 0,

12x

+ 2λy = 0, 6x + 2y

+ y2

= 25

+ y

2 = 25

4x2

4x2

− x

− 4λx

y =

,

6

− x − 4λx

− x −

4λx

6x + 2

+ λ

= 0,

6

6

4x2 + y2 = 25

− x −

4λx

− x − 4λx

y =

6

,

y =

6

,

1+ 4λ

1+ 4λ

1+

4λ

6x

− 2x

− λx

= 0,

x

6 − (2 + λ)

= 0,

6

6

6

2

+ y

2

= 25

2

+ y

2

= 25

4x

4x

99

y = − x − 4λx ,					− x −	4λx
			y =		6	,
	6
		36 − (2 + λ)(1+ 4λ) = 0,		= 0 или 34 − 9λ − 4λ 2 = 0,
x = 0 или			x
	+ y2 = 25				+ y2	= 25.
4x2			4x2
При x = 0		из первого уравнения получим,				что y = 0. Но тогда

третье уравнение данной системы не имеет смысла. Следовательно,

				− x − 4λx								− x − 4λx
			=					y =											,
	y					6	,								6
																									17
	34			− 9λ − 4λ 2 = 0,					λ = 2,λ 2										= −										,
				+ y2 = 25					1																		4
	4x2								4x	2		+ y			2	= 25.
														λ 2		= −							17
				λ1 = 2,																								,
																								4
			y =			−3x									y =						8x
							,	или																	,
						2													3
		2			−3x		2						2			8x								2
4x			+				= 25		4x					+											=					25
						2										3
																17
						λ1 = 2,			λ 2			= −								,
																4
							= 3,				y = ±4,
						y		или
						x = ±2					x = ±					3	.
																2
Следовательно,					M2(2, −3),			M3(−2, 3),				M4(3/2, 4)																и		M5(−3/2, −4) −

стационарные точки. Точки M2(2, −3) и M5(−3/2, −4) не принадлежат границе G1, следовательно, находить значение функции в этих точках не надо.

Найдем значение функции в стационарных точках M3(−2, 3)

и M4(3/2, 4) и в граничных точках А(−5/2, 0) и В(5/2, 0):

z(−2, 3) = 4 − 12 · 6 + 2 · 9 = −50;

100