динамик тема 2

Институт машиностроения и транспорта

Кафедра теоретической механики

ДИНАМИКА

ТЕМА 2. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ

Методические указания для выполнения контрольной работы

по дисциплине «Теоретическая механика» для студентов заочной формы обучения

	K	D	cos30º
			r
	30º
		r	VD
			r	h
В	О		R–
	R

V F N

R

P	1,5R	А

Новокузнецк

2012

УДК 531 (075) Д46

Рецензент

доктор технических наук, профессор, зав. кафедрой сопротивления материалов и строительной механики СибГИУ А.Н. Никитин

Д46 Динамика. Тема 2. Теорема об изменении кинетической энергии материальной точки: метод. указ. / Сиб. гос. индустр. ун-т ; сост. : Т.Н. Дадочкина. – Новокузнецк : Изд. центр СибГИУ,

2012. – 23 с.

Представлены методические указания для выполнения самостоятельной контрольной работы по дисциплине «Теоретическая механика», раздел «Динамика», тема 2. Теорема об изменении кинетической энергии материальной точки. Излагается краткая теория, приведены варианты контрольных заданий, методические указания для их выполнения, пример выполнения и оформления задачи.

Предназначены для студентов заочной формы обучения направлений подготовки «Строительство», «Горное дело», «Технологические машины и оборудование», «Технология транспортных процессов», «Электроэнергетика и электротехника».

2

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ

			1 Краткая теория
	Кинетической энергией материальной точки называется ска-
		mV 2
	лярная величина		, равная половине произведения массы точки
		2

на квадрат ее скорости.

Единицей измерения кинетической энергии в СИ является джоуль (1 Дж = 1 Н м).

1.1 Элементарная работа силы

Элементарная работа dA силы F на элементарном (бесконеч-

но малом) перемещение dS определяется выражением:
dA Fτ ds,	(1)

где F − проекция силы F на направление скорости точки приложе-

ния силы или на направление элементарного перемещения, которое совпадает с направлением

z

скорости точки (рис. 1).

М ds F

Элементарная

работа

силы

является скалярной величиной.

М1

V

Так как F F cos , где −

М2

k

r

угол между силой

F и направле-

нием вектора скорости точки V , то

F

О

y

выражение (1) можно представить

i

j

в виде:

x

dA F cos ds.

Рисунок 1 – Элементарная работа

(2)

силы

В этой формуле знак элементарной работы определяется знаком cos : если < 90 , то работа положительная, если > 90 − работа отрицательная.

Отметим частные случаи, которые можно получить из (2):

3

= 0 , dA = F dS; = 90 , dA = 0; = 180 , dA = −F dS.

Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю.

Приведем другие формулы для вычисления элементарной рабо-

ты силы. Из

кинематики

точки

известно,

что V

/ dt,

dr

V

dS / dt.

Следовательно,

dS

d

Vdt. Согласно уравнению

V

r

(2), элементарная работа:

dA F

d

.

d

cos F

(3)

r

r

Элементарная работа силы равна скалярному произведению вектора силы на дифференциал радиус-вектора точки приложения силы.

Если силу F и радиус-вектор r разложить по осям координат, то из формулы (3) следует выражение элементарной работы:

dA Fxdx Fydy Fzdz,

(4)

где Fx, Fy, Fz − проекции силы на координатные оси,

dx, dy, dz − дифференциалы координат точки приложения силы.

1.2 Полная работа силы

Работа силы на любом конечном перемещении М1М2 вычисляется как предел интегральной суммы соответствующих элементарных работ, т.е. равна взятому вдоль этого перемещения интегралу от элементарной работы.

Пределы интеграла соответствуют значениям переменных интегрирования в точках М1 и М2 (рис. 1):

n		M2				M2		M2
A lim dAk				dAk				Fτ dS		(Fхdx Fуdу Fz dz).	(5)
n k 1		M	1			M	1	M	1

1.3 Работа постоянной силы

Работа постоянной силы (по модулю и направлению) на прямолинейном перемещении точки ее приложения вычисляется как ска-

4

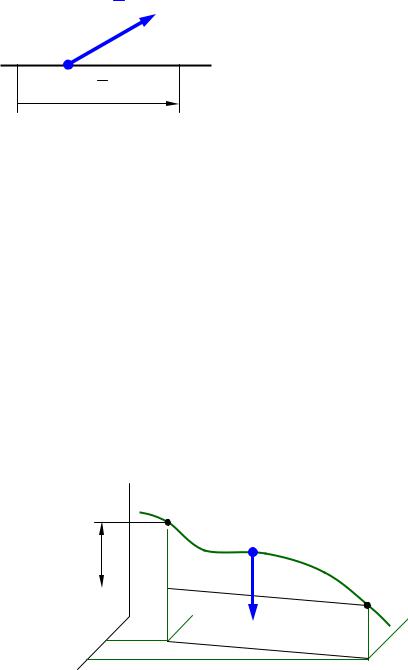
лярное произведение вектора силы на вектор перемещения точки

(рис. 2):

A(F		) F S FS cos .					(6)

F

S

Рисунок 2 – Работа постоянной силы

Если направление вектора силы совпадает с перемещением точки еѐ приложения, т.е. = 0, то работа запишется:

		) FS.	(7)
A(F

Работа силы на прямолинейном перемещении точки еѐ прило-

жения равна алгебраическому значению произведения проекции силы на направление перемещения на перемещение.

1.4 Работа силы тяжести

Работа силы тяжести равна произведению модуля силы на разность высот точки ее приложения (рисунок 3):

h

А(		) mg(z0 z1 ).	(8)
	P

z

М0(x0, y0, z0)

							М(x, y, z)
		z0
				P				М1(x1, y1, z1)
О									y
			х0				z1
								x1
	у0
				y1

Рисунок 3 – Работа силы тяжести

Обозначим h (z0 z1 ), тогда:

A mgh.

(9)

5

Если на рассматриваемом перемещении точка приложения силы опускается (z0 > z1 и h = z0 − z1 положительно), то работа силы тяжести положительна. Если же поднимается (z0 < z1 и h = z0 − z1 отрицательно), то работа силы тяжести отрицательна.

Из полученного результата следует, что работа силы тяжести не зависит от вида траектории, по которой перемещается точка ее приложения.

1.5 Работа силы упругости

Работа силы упругости равна половине произведения коэффициента упругости на разность квадратов начальной и конечной деформации пружины (рисунок 4):

			c( 2	2 )
A(F )
			1	2	.	(10)
				2

Если начальная деформация пружины 1 = 0, то работа упругой силы вычисляется по формуле:

l0

с 2

A(F )

.

(11)

M1 F

M

M2

M

0

2

х

Работа упругой

силы

О

1

х

отрицательна

при

любой

деформации

(растяжении

2

или сжатии) и положи-

тельна при

возвращении

Рисунок 4 − Работа упругой силы

на прямолинейном перемещении

пружины в исходное неде-

формированное состояние.

1.6 Работа равнодействующей

Если к движущейся точке приложено несколько сил (рисунок 5), то работа равнодействующей этой системы сил на каком-либо перемещении точки равна алгебраической сумме работ каждой силы на этом перемещении:

6

A(

n

R

) A(Fk ) A(F1 ) A(F2 )

... A(Fk ) ... A(Fn ). (12)

k 1

где Fk – силы, приложенные к точке,

n

R

Fk

− равнодействующая сходящейся системы сил.

k 1

F1

F2

М1

М

М0

F

3

Fn

Рисунок 5 – Работа равнодействующей

1.7 Работа силы на конечном перемещении

Если точка приложения постоянной силы F , получила ряд по-

следовательных перемещений

Sk , то работа силы на результирую-

щем перемещении S равна алгебраической сумме работ силы на ка-

ждом перемещении (рисунок 6):

A(F

) F S F S1 F S2

... F Sk ... F Sn

(

1

2 ...

k ...

n ).

(13)

F

S

S

S

S

М1

S2

S1

М2

М0

F

Sk

S

М

Мk

S

n

n

Рисунок 6 – Работа силы на конечном перемещении

1.8 Теорема об изменении кинетической энергии точки

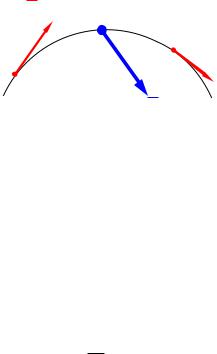
Изменение кинетической энергии точки на каком-либо перемещении равно сумме работ всех сил, приложенных к точке, на том же перемещении (рисунок 7):

7

2	2		A(F ),			(14)
mV2	mV1
			n
				k
2	2
			k 1

где V1 – скорость точки в начальном положении, V2 – скорость точки в конечном положении.

V1 М

М2

М1
	V
	2

R

Рисунок 7 – Теорема об изменении кинетической энергии точки

2 Контрольные задания

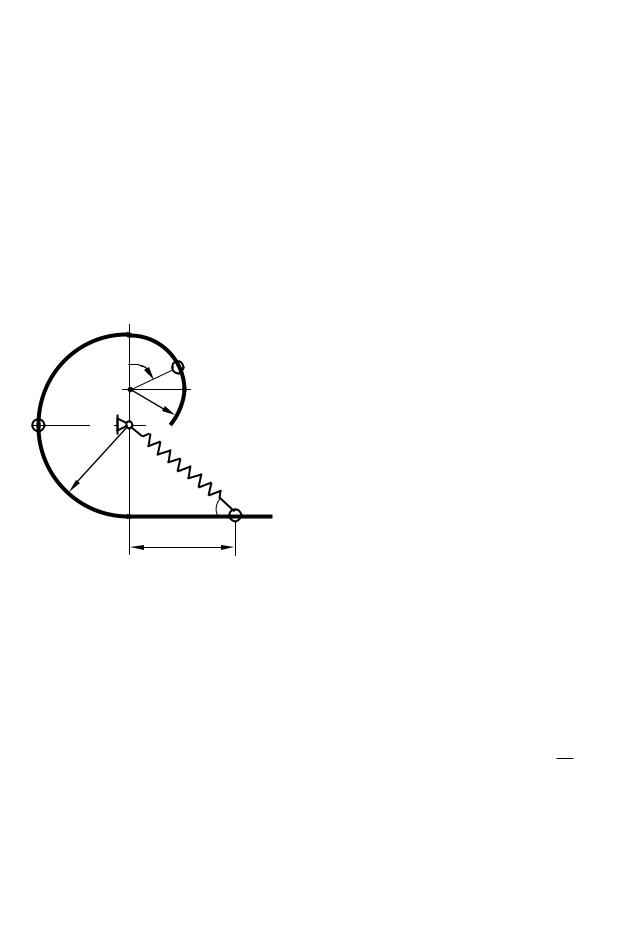
Тонкий гладкий стержень, расположенный в вертикальной плоскости, изогнут так, что состоит из прямолинейного участка и двух дуг окружностей радиусом R = 0,5 м, r = 0,6R м, сопряженных в точке K. На стержень нанизан шар весом Р, прикрепленный к пружине с ко-

эффициентом жесткости c k PR . Другой конец пружины закреплен в

точке О. Длина пружины в недеформированном состоянии равна l0. Шар начинает двигаться из положения А, определяемого углом

без начальной скорости (в вариантах 0, 1, 10, 17, 18 ‒ этот угол определяется по заданным линейным размерам). Достигнув точки В, показанной на рисунке, шар освобождается от пружины и дальше движется только под действием силы тяжести.

Считая шар материальной точкой, определить, какую скорость он будет иметь, придя в точку D.

Варианты контрольных заданий представлены на страни-

цах 12–21.

Примечания

1. Номер варианта соответствует сумме двух последних цифр

шифра.

2. Номер строки из таблицы в каждом варианте равен последней

цифре шифра.

8

			3 Методические указания
	Задача Д-2 – на применение теоремы об изменении кинетиче-
ской энергии материальной точки (14). При решении задачи теорему
можно применять сразу на всем перемещении, совершаемом шаром
от начального положения А до положения, в котором нужно опреде-
лить скорость D.
	Рисунок необходимо делать в масштабе в соответствии с задан-
ными в варианте параметрами.
	4 Пример решения и оформления задачи
	K				Тонкий гладкий стержень, распо-
					ложенный в вертикальной плоскости,
			D		изогнут так, что состоит из прямоли-
					нейного участка и двух дуг окружно-
			r		стей радиусом R = 0,8 м, r = 0,6R м,
В	О				сопряженных в точке K (рисунок 8).
	R				На стержень нанизан шар весом Р,
					прикрепленный к пружине с коэффи-
					циентом жесткости с. Другой конец
			1,5R	А	пружины закреплен в точке О. Длина
					пружины в недеформированном со-
Рисунок 8 – Условие задачи					стоянии равна l0.
					Шар начинает двигаться из по-
ложения А, определяемого углом без начальной скорости. Достиг-
нув точки В, показанной на рисунке, шар освобождается от пружины
и дальше движется только под действием силы тяжести.
	Считая шар материальной точкой, определить, какую скорость
он будет иметь, придя в точку D.
	Дано: Р, l	0	= 0,9R,	V	= 0, R = 0,8 м, r = 0,6R, c k P (k 6),
				A	R
= 30º.
	Определить: VD.
					Решение.
	1. Выполняем расчетную схему задачи, для этого рисунок сдела-
ем в масштабе в соответствии с заданными в варианте размерами и
углами (рисунок 9).

9

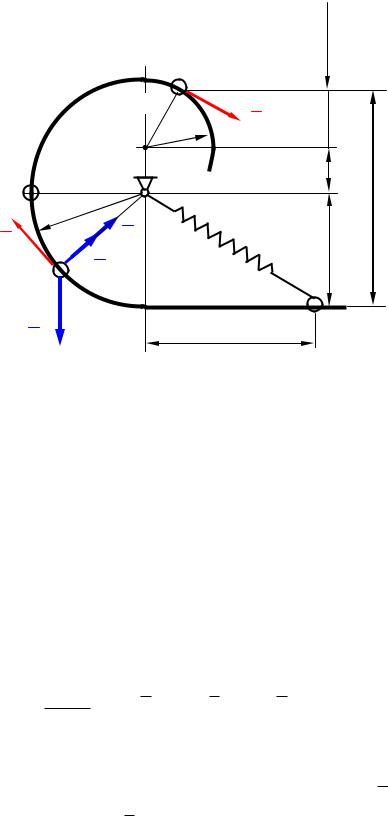
Для определения скорости шарика в точке D, рассмотрим его в произвольном положении и изобразим действующие на него силы:

P – сила тяжести;				N – опорная реакция; F – сила упругости пружи-
ны,			дейст-							вующая
на			участке						cos30º	АВ.
						K
							D		r

30º

r VD

	В	О
		R

V F

N

R– r	h
R

P	1,5R	А

Рисунок 9 – Расчетная схема задачи

Для решения задачи применяем теорему об изменении кинетической энергии материальной точки:

2	2		A(F ) или			2	2		A(P) A(N) A(F ).
mVD mVA						mVD mVA
			n
				k
2	2					2	2
			k 1

Так как шарик движется без начальной скорости (VA = 0), то теорема принимает вид:

mV 2

2

D A(P) A(N) A(F ). (15)

Вычислим работы сил, действующих на шарик.

Так как реакция перпендикулярна перемещению A(N ) 0. Работа силы тяжести: A(P) Ph,

10