
Числовые ряды 2
.doc
Теорема 2.7.
(Обобщенный признак Коши).
Если существует верхний предел
![]() ,
то при
,
то при
![]() ряд сходится, а при
ряд сходится, а при
![]() ряд расходится.
ряд расходится.
Пример 14. Исследуем
на сходимость ряд
![]() .
.
Первая мысль при
рассмотрении данного ряда, – применить
признаки Коши и Даламбера. Но оба предела
![]() и
и
![]() не существуют. Однако верхний предел
не существуют. Однако верхний предел
![]() существует и меньше единицы. По общему
признаку Коши, данный ряд сходится.
существует и меньше единицы. По общему
признаку Коши, данный ряд сходится.
Напомним читателю,
что из любой ограниченной последовательности
![]() можно выделить сходящуюся
подпоследовательность, предел которой
называется частичным пределом. Таких
подпоследовательностей может быть
несколько. Наибольшей частичный предел
(он всегда существует в случае ограниченной
последовательности) называется верхним
пределом
данной последовательности. В частности,
в данном примере из подпоследовательности
можно выделить сходящуюся
подпоследовательность, предел которой
называется частичным пределом. Таких
подпоследовательностей может быть
несколько. Наибольшей частичный предел
(он всегда существует в случае ограниченной
последовательности) называется верхним
пределом
данной последовательности. В частности,
в данном примере из подпоследовательности
![]() можно выделить подпоследовательность
можно выделить подпоследовательность
 ;
её предел будет верхним.
;
её предел будет верхним.
Замечание.
В обеих теоремах случай
![]() включается в
включается в
![]() .
.
Замечание.
Если
![]() ,
то ряд может сходится, а может расходится.
Поэтому признаки Коши и Даламбера не
подходят и необходимо использовать
другие признаки.
,
то ряд может сходится, а может расходится.
Поэтому признаки Коши и Даламбера не
подходят и необходимо использовать
другие признаки.
Пример. 14. Рассмотрим
гармонический ряд
![]() .
Известно, что он расходится. Покажем,
что
.
Известно, что он расходится. Покажем,
что
![]() .
Рассмотрим
.
Рассмотрим
![]()

![]()
![]() .
.
Пример. 15. Рассмотрим
ряд
![]() .
.
Выяснить сходимость
этого ряда признаком Даламбера не
удается, так как
![]() и
и
![]() .
.
Найдем сумму ряда по определению. Заметим, что
![]() .
.
Тогда исходный ряд можно записать в виде:
![]() .
.
Частичная сумма
первых
![]() членов после раскрытия скобок и сокращения
будет равна
членов после раскрытия скобок и сокращения
будет равна
![]() .
Следовательно,
.
Следовательно,
![]() ,
то есть ряд сходится.
,
то есть ряд сходится.
Пример 16. Рассмотрим
ряд
![]() .
.
![]() .
.
Этот ряд сходится,
так как
![]() ,
а ряд
,
а ряд
![]() сходится из примера 15, значит ряд тоже
сходится по первому признаку сравнения
сходится из примера 15, значит ряд тоже
сходится по первому признаку сравнения
![]() .
.
И наконец, сформулируем еще один признак сходимости, который связывает сходимость ряда со сходимостью некоторого несобственного интеграла.
Теорема 2.8.
(Интегральный признак Коши).
Пусть
![]() – знакоположительный ряд,
– знакоположительный ряд,
![]() – непрерывная, неотрицательная, монотонно
убывающая на некотором промежутке
– непрерывная, неотрицательная, монотонно
убывающая на некотором промежутке
![]() (где
(где
![]() )
функция, такая, что
)
функция, такая, что
![]() (для любого
(для любого
![]() ).
Тогда несобственный интеграл
).
Тогда несобственный интеграл
![]() и ряд
и ряд
![]() ведут себя одинаково относительно
сходимости.
ведут себя одинаково относительно
сходимости.
Доказательство.
Изобразим члены
ряда геометрически, откладывая по оси
абсцисс номера
![]() членов ряда, а по оси ординат –
соответственно значения
членов ряда, а по оси ординат –
соответственно значения
![]() членов ряда. Построим на том же чертеже
график невозрастающей функции
членов ряда. Построим на том же чертеже
график невозрастающей функции
![]() ,
удовлетворяющей условиям
,
удовлетворяющей условиям
![]() .
Получим, что площадь любого прямоугольника
.
Получим, что площадь любого прямоугольника
![]() равна
равна
![]() ,
и следовательно,
,
и следовательно,
![]() – частичная сумма ряда равна сумме
площадей построенных прямоугольников.
Рассмотрим ступенчатую фигуру,
образованную этими прямоугольниками.
Она закрывает область, ограниченную
кривой
– частичная сумма ряда равна сумме
площадей построенных прямоугольников.
Рассмотрим ступенчатую фигуру,
образованную этими прямоугольниками.
Она закрывает область, ограниченную
кривой
![]() и прямыми
и прямыми
![]() .
Площадь этой области равна
.
Площадь этой области равна
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Рассмотрим теперь
Рис. 2. Здесь первый слева из прямоугольников
имеет высоту
![]() ,
второй
,
второй
![]() и т.д. Площадь последнего из построенных
прямоугольников равна
и т.д. Площадь последнего из построенных
прямоугольников равна
![]() .
Следовательно, площадь всех построенных
прямоугольников равна сумме всех членов
ряда, начиная от второго до
.
Следовательно, площадь всех построенных
прямоугольников равна сумме всех членов
ряда, начиная от второго до
![]() –го,
то есть
–го,
то есть
![]() .
С другой стороны, ступенчатая фигура,
образованная этими прямоугольниками
содержится внутри кривой фигуры,
ограниченной кривой
.
С другой стороны, ступенчатая фигура,
образованная этими прямоугольниками
содержится внутри кривой фигуры,
ограниченной кривой
![]() и прямыми
и прямыми
![]() .
Получаем
.
Получаем
![]()
![]()
![]() .
.
Рассмотрим два случая:
-
Интеграл
 – сходится,
то есть имеет конечное значение, так
как
– сходится,
то есть имеет конечное значение, так
как

 .
.
Так как сумма
![]() – ограниченна,
и при любых
– ограниченна,
и при любых
![]() ,
при
,
при
![]() возрастает (учитывая, что
возрастает (учитывая, что
![]() )
то, существует
)
то, существует
![]() и тогда по определению сходящегося
ряда, ряд сходится.
и тогда по определению сходящегося
ряда, ряд сходится.
-
 – расходится. Это
означает, что
– расходится. Это
означает, что неограниченно
возрастает при
неограниченно
возрастает при
 и тогда, в силу неравенства
и тогда, в силу неравенства
 ,
,
 – неограниченно
возрастает при возрастании
– неограниченно
возрастает при возрастании
 .
Значит ряд расходится. Теорема доказана.
.
Значит ряд расходится. Теорема доказана.
Замечания.
-
Признак основан на сравнении рядов с несобственными интегралами.
-
Функцию
 ,
принимающую в точках
,
принимающую в точках
 значения
значения
 ,
чаще всего удается построить с помощью
замены натурального
,
чаще всего удается построить с помощью
замены натурального
 в выражении
в выражении
 ,
чаще на непрерывно изменяющийся аргумент
,
чаще на непрерывно изменяющийся аргумент
 .
Так, например, если
.
Так, например, если
 ,
то
,
то
 ;
если
;
если
 ,
то
,
то
 .
Однако, не всегда таким путем можно
получить функцию
.
Однако, не всегда таким путем можно
получить функцию
 .
Если, например
.
Если, например
 ,
то в этом случае нельзя заменить
,
то в этом случае нельзя заменить
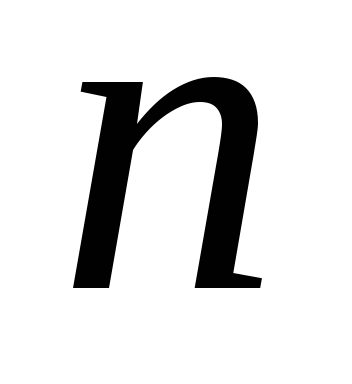 на
на
 ,
так как символ
,
так как символ
 при нецельных
при нецельных
 лишен смысла. Это не означает, что не
существует функции
лишен смысла. Это не означает, что не
существует функции
 ,
принимающей в точках
,
принимающей в точках
 значения
значения
 .
Напротив, она всегда существует, но ее
аналитическое выражение не всегда
просто найти.
.
Напротив, она всегда существует, но ее
аналитическое выражение не всегда
просто найти. -
Достоинство интегрального признака Коши состоит в том, что он четко проводит различие между все более медленно сходящимися рядами, даже если члены одного из них лишь незначительно отличаются от членов другого, что иллюстрируется приведенным ниже примером 17.
-
Интегральный признак Коши применим к рядам, в которых положительные члены монотонно убывают с увеличением их номера. Но даже и для таких функций может оказаться, что путь непосредственного вычисления интеграла при применении интегрального признака сходимости не всегда приемлем. Например, для ряда
 требуется вычислить интеграл
требуется вычислить интеграл
 ,
что затруднительно. К данному ряду
очевидно применение первого признака
сравнения: при
,
что затруднительно. К данному ряду
очевидно применение первого признака
сравнения: при
 мы имеем
мы имеем
 ,
а ряд
,
а ряд
 сходится как геометрическая прогрессия
со знаменателем
сходится как геометрическая прогрессия
со знаменателем
 .
.
Пример 17. Исследовать
на сходимость ряд
![]() (
(![]() ).
).
Рассмотрим функцию
![]() .
Эта функция на промежутке
.
Эта функция на промежутке
![]() непрерывна, неотрицательна, монотонно
убывает. Кроме того, для любого натурального
непрерывна, неотрицательна, монотонно
убывает. Кроме того, для любого натурального
![]()
![]() .
.
Следовательно,
несобственный интеграл
![]() и ряд
и ряд
![]() ведут себя одинаково относительно
сходимости. Рассмотрим указанный
несобственный интеграл. Имеем
ведут себя одинаково относительно
сходимости. Рассмотрим указанный
несобственный интеграл. Имеем
![]()
![]() .
.
Так как по условию
![]() ,
то
,
то
![]() .
Но тогда
.
Но тогда
![]() при
при
![]() и
и ![]()
![]() .
.
Итак, получили,
что несобственный интеграл
![]() при
при
![]() сходится. Следовательно, ряд
сходится. Следовательно, ряд
![]() (
(![]() )
тоже сходится.
)
тоже сходится.
Пример 18. Исследуем
сходимость ряда
![]() интегральным признаком Коши.
интегральным признаком Коши.
По формуле общего
члена введем функцию
![]() .
Она непрерывна и монотонно убывает на
промежутке
.
Она непрерывна и монотонно убывает на
промежутке
![]() .
Вычислим несобственный интеграл
.
Вычислим несобственный интеграл
![]() .
.
Интеграл расходится, поэтому расходится и ряд.
При исследовании
сходимости ряда
![]() с положительными членами иногда
используется метод выделения главной
части. Он применяется там, где удается
получить с помощью формулы Тейлора
асимптотическую формулу вид
с положительными членами иногда
используется метод выделения главной
части. Он применяется там, где удается
получить с помощью формулы Тейлора
асимптотическую формулу вид
![]() .
В этом случае ряд
.
В этом случае ряд
![]() сходится или расходится одновременно
с обобщенным гармоническим рядом
сходится или расходится одновременно
с обобщенным гармоническим рядом
![]() (см пример 17).
(см пример 17).
Пример 18. Исследовать
на сходимость ряд
 .
.
Так как
![]() при
при
![]() ,
то
,
то
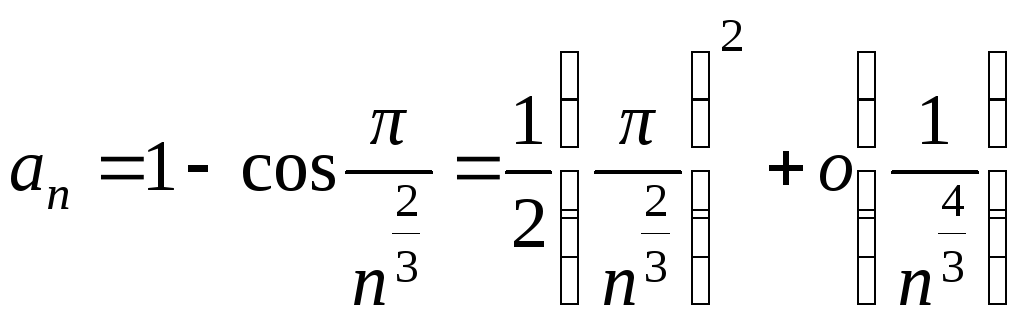 ,
,
откуда
 .
Следовательно, ряд
.
Следовательно, ряд
 сходится.
сходится.
При оценке
факториалов больших чисел и вычислении
пределов, содержащих
![]() бывает полезна формул Стиглинга:
бывает полезна формул Стиглинга:
 ,
которая означает, что
,
которая означает, что
 .
.
Пример 19. Исследовать
сходимость ряда
![]() .
.
Применение признака
Даламбера в данном случае затруднительно.
Используем радикальный признак Коши и
заменим
![]() по формуле Стирлинга на
по формуле Стирлинга на
 .
.
 .
.
Ряд расходится.
§3. Некоторые применения теория числовых рядов
-
Исследование сходимости несобственных интегралов с бесконечными пределами основано на использовании интегрального признака Коши.
Пример 1. Исследовать
на сходимость
![]() .
.
Функция
![]() непрерывна и положительна для
непрерывна и положительна для
![]() .
Составим ряд
.
Составим ряд
 .
Он сходится по признаку Даламбера, так
как
.
Он сходится по признаку Даламбера, так
как
 .
.
Из сходимости ряда вытекает сходимость данного интеграла.
-
Достаточные признаки можно использовать для доказательства равенств вида
 .
.
Пример 2. Доказать,
что
![]() .
Обозначим
.
Обозначим
![]() ,
,
![]() .
Составим ряд
.
Составим ряд
![]() .
Исследуем его сходимость признаком
Даламбера:
.
Исследуем его сходимость признаком
Даламбера:
![]() .
.
Так как ряд с общим
членом
![]() сходится, то
сходится, то
![]() по необходимому признаку сходимости.
по необходимому признаку сходимости.
