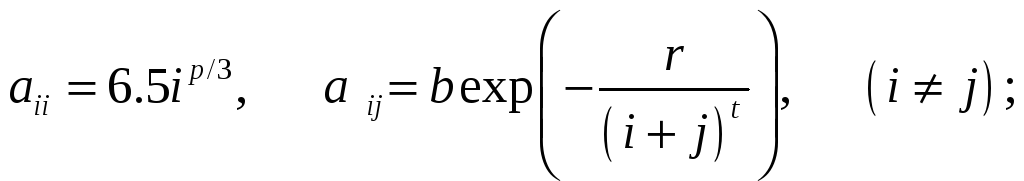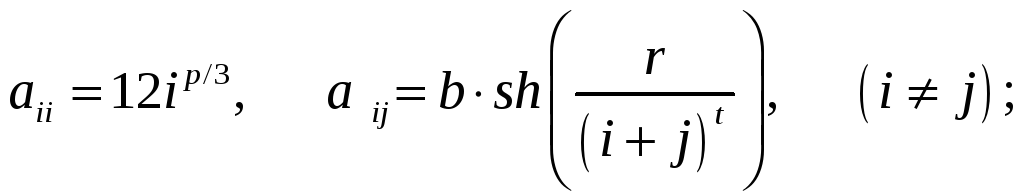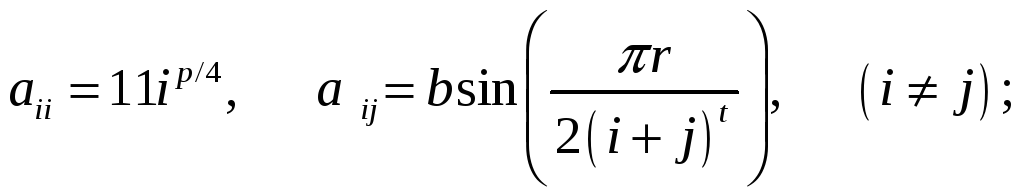3 семестр / Задание №1 Частичная проблема собственных значений

Задание №1

ЧАСТИЧНАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ

Цель работы: изучение частичной проблемы собственных значе­ний, вычисление максимального собственного значения самосопряжен­ной матрицы.

ПОСТАНОВКА ЗАДАЧИ

Пусть А - квадратная матрица размера n*n. Частичной проб­лемой собственных значений называется нахождение некоторой части собственных значений λ и, возможно, соответствующих собственных векторов х матрицы А из однородного уравнения

А х = λ х.

Одной из задач проблемы собственных значений является рассматривае­мая в данной работе задача нахождения максимального по модулю собственного значения матрицы А.

Далее будем полагать, что А - действительная симметричная мат­рица. Самосопряженная матрица А имеет полную систему (базис) ортогональных нормированных собственных векторов e_i (i= 1,2,...,n), являющихся решением задачи

Ae_i=λ_ie_i,

_,

где - символ Кронекера. Предположим также, что максимальное собственное значение матрицы А - простое (не кратное).

Тогда λ₁(А) можно найти с помощью следующего итерационного процесса, называемого степенным методом:

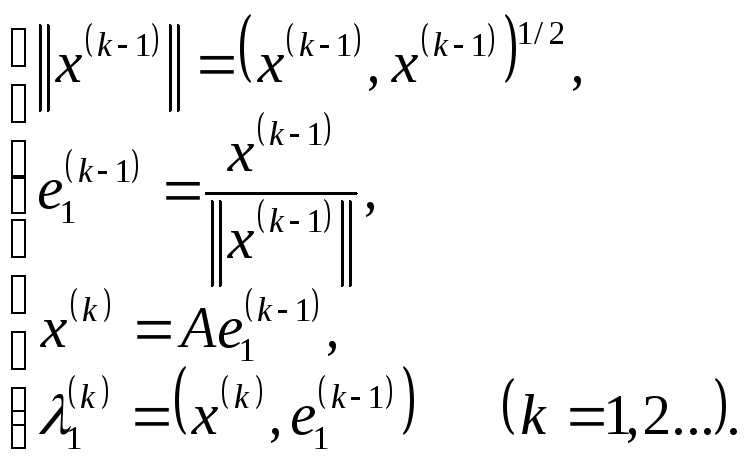
Здесь k - номер итерации, а в качестве x⁽⁰⁾ принимается произвольный, например случайный вектор. При итерационный процесс сходится линейно, т.е.

со скоростью геометрической прогрессии, имеющей знаменатель где λ₂(А) - следующее по модулю собственное значение матрицы А.

Если значения |λ₂(А)| и |λ₁(А)| близки, то сходимость будет медленной.

Смысл данного итерационного процесса можно пояснить следующим образом. Поскольку собственные векторы в нашем случае образуют полную систему, то любой вектор можно представить в виде

где x_i – собственные векторы, а с_i – константы.

Умножим обе части равенства на матрицу А

Производя такое умножение k раз, получим

Таким образом, после k умножений вектор y имеет компоненту вдоль каждого собственного вектора, пропорциональную k –ой степени соответствующего значения λ_i.

Теперь, если для i =2,3,….,n, то при k→∞

т.е. вектор y оказывается почти коллинеарен собственному вектору x₁.

Рассмотрим отношение

Можно ожидать, что в пределе каждая компонента нашего вектора будет умножаться на одно и то же число λ_i. На практике рекомендуется нормировать получающийся вектор на каждом шаге так, чтобы наибольшая его компонента была равна 1.

На последнем шаге нормирующий множитель даст величину наибольшего по модулю собственного значения. При этом заодно получается и собственный вектор.

ВАРИАНТЫ ЗАДАНИЙ

(n=5÷10; p,q=1÷4; r,t=0.1÷1.2; b=0.01÷0.1)

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

ПРОГРАММИРОВАНИЕ

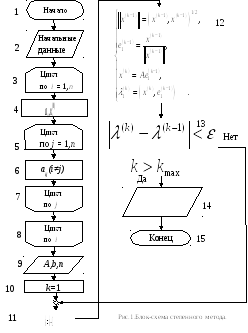
Блок-схема программы представлена на Рис.1. В циклах 3-8 вычисляются элементы матрицы A и начальный вектор x⁽⁰⁾, в блоках 10-13 реализован степенной метод, в блоках 9,14 выводятся промежуточные и конечные результаты.

В качестве x⁽⁰⁾ следует принять случайный вектор, элементы которого представляет собой случайные числа, равномерно распределенные в интервале (0,1). Для выработки таких чисел в программном обеспечении компьютера имеется специальный генератор (датчик). Итерации следует заканчивать при выполнении какого-либо из двух условий

где ε= 0.1÷0.001 - заданная погрешность, k_max- максимальное число итераций. Окончание итераций при выполнении последнего условия означает, что за k_max итераций заданная погрешность не достигнута.

Проверку программы рекомендуется провести на тестовой диагональной матрице с элементами

a_ii=i, a_ij=0 (i,j=1,2,…,n),

для которой

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• формулы для конкретного варианта;

• текст программы;

• результаты решения: исходная матрица, значение λ₁(A) и число итераций k.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что понимается под частичной проблемой собственных значений?

2. Как строятся степенной метод вычисления максимального по модулю собственного значения?

3. Какие методы решения полной проблемы собственных значений вы знаете?

4. Что такое характеристический полином?