3 семестр / Задание №4 Численное решение задачи коши для обыкновенных дифференциальных уравнений

Задание №4

ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Цель работы — изучение численных методов решения систем обыкновенных дифференциальных уравнений, решение задачи Коши для систем двух уравнений методом Рунге—Кутта второго порядка.

ПОСТАНОВКА ЗАДАЧИ

Решение простейшего обыкновенного дифференциального уравнения

(1)

начиная с некоторого момента t=t₀ имеет вид

(2)

То есть очевидна связь между задачами интегрирования и решения дифференциальных уравнений. Однако есть и существенные отличия. Одно из важнейших заключается в том, что при интегрировании результатом является единственное число — величина интеграла, а решая дифференциальное уравнение мы ищем функцию, определённую на некотором отрезке.

Поскольку функция может быть вычислена лишь в конечном числе точек (компьютер не может выполнить бесконечное число операций), то при численном интегрировании дифференциальных уравнений необходимо перейти от непрерывного решения на отрезке к дискретному. Таким образом решение будет вычисляться лишь в конечном числе точек t_i (в фиксированные моменты времени, если t - время), а не на всём непрерывном отрезке. , где - шаг интегрирования.

Простейшим методом решения дифференциальных уравнений является метод Эйлера, основанный на предположении, что правая часть уравнения (1) слабо изменяется на шаге интегрирования, то есть в (2) f(τ)=const . Иными словами решение можно получить, используя для численного интегрирования в (2) метод прямоугольников:

(3)

.

К формуле (3) можно также прийти, разложив функцию в точке t_i в ряд Тейлора с шагом и отбросив все члены с производной выше первого порядка. Оценивая остаточный член разложения, можно сделать вывод о том, что метод Эйлера имеет первый порядок погрешности относительно шага интегрирования, то есть уменьшение шага интегрирования вдвое, приводит к такому же уменьшению погрешности.

Точность метода можно увеличить, оставляя в разложении в ряд Тейлора члены со второй производной и т.д.

Одним из наиболее распространенных методов численного решения задачи Коши для систем обыкновенных дифференциальных уравнений вида

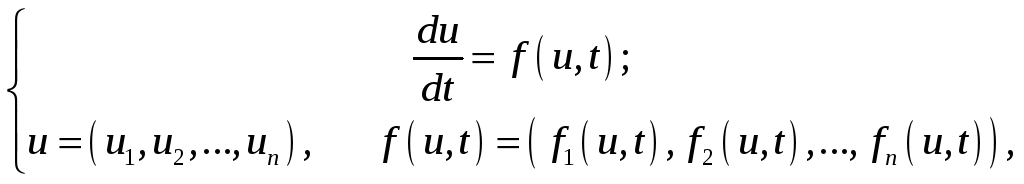
u(t°) = u°,

является метод «предиктор—корректор» второго порядка. В этом методе решение на каждом временном шаге τ склады­вается из двух этапов:

Первый этап («предиктор»), на котором вычисляется предварительное значение на половинном шаге

u⁺= u + f.

Второй этап («корректор»), на котором вычисляется окончательное значение на следующем шаге

Здесь обозначено

u = u(t), u⁺=u(t+),

Описанный метод относится к методам типа Рунге—Кутта. Поскольку он имеет на шаге погрешность О(∆t³), а на всем интервале интегрирования — погрешность О(∆t²), его называют также методом Рунге—Кутта второго порядка.

ВАРИАНТЫ ЗАДАНИЙ

1. Вычислить траекторию заряженной частицы с зарядом q и массой покоя т₀ в потенциальном поле φ(х).

Формулы уравнений движения:

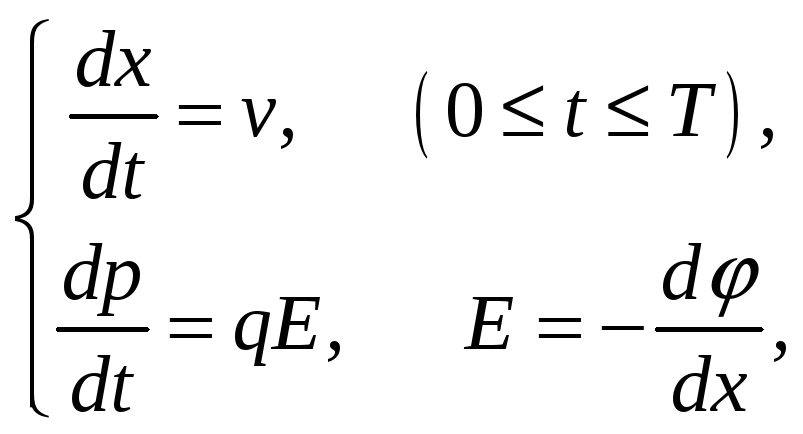
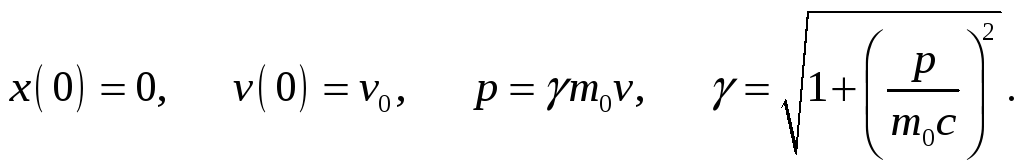
Сорта частиц: электроны, протоны, α - частицы.

ВАРИАНТЫ ЗАВИСИМОСТЕЙ φ(х)

(σ,r,s=1÷3; φ₀=±(100÷1000), v₀=(0.5÷1)10⁶, τ=10^-12÷10^-8)

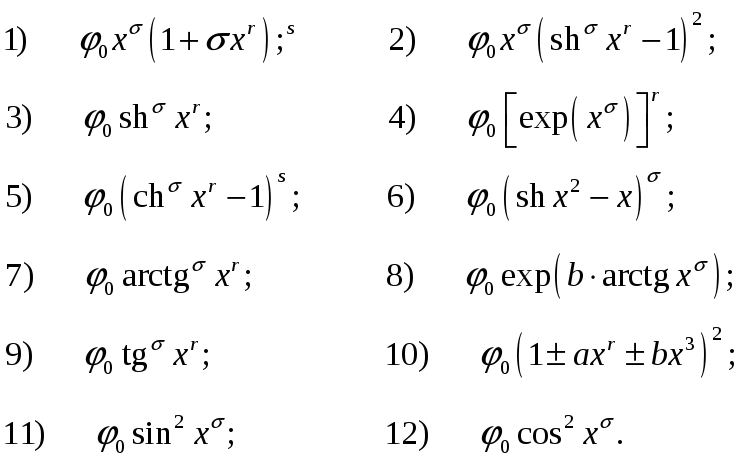
1. Вынужденные колебания в электрическом RLC-контуре описываются системой обыкновенных дифференциальных уравнений

Здесь R — сопротивление, L — индуктивность, С — ёмкость контура; Q — заряд на конденсаторе, I — ток в контуре, ω₀ — собственная частота контура, β — коэффициент затухания, E — вынуждающая сила, β = 0÷0.2, ω_о=1÷2, Q₀=l÷10, τ=0.05·2π/ω₀.

Промоделировать колебания в контуре.

ВАРИАНТЫ ЗАВИСИМОСТЕЙ E(Q, I, t)

(р,q,r,s=0÷3; ω=1÷4, φ_о=-π/2÷π/2)

1) (a+b|Q|^p+c|I|^q) t^r sin(ωt+φ₀);

2) (a+b|Q|^p+c|I|^q+d|QI|^s) t^r sin(ωt+φ₀);

3) a|Q|^p |I|^q e^±rt sin(ωt+φ₀);

4) a|Q|^p |I|^q t^r sin(ωt+φ₀);

5) (a+b|Q|^p+c|I|^q) e^±rt sin(ωt+φ₀);

6) (a+b|Q|^p+c|I|^q+d|QI|^s) e^±rt sin(ωt+φ₀).

ПРОГРАММИРОВАНИЕ

Блок-схема программы для первого варианта задания приведена на Рис.1. Метод «предиктор—корректор» второго порядка реализован в блоке 5. Зависимости координаты и импульса частицы накапливаются в одномерных массивах x(i),p(i) и затем используются для построения фазовых траекторий.

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• формулы и параметры для конкретного варианта;

• текст программы;

• результаты решения, графики зависимостей.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Как выполняется решение систем обыкновенных дифференциальных уравнений методом "предиктор-корректор"?

2. Каковы особенности метода Рунге—Кутта второго порядка?

3. Какие ещё существуют методы численного решений систем обыкновенных дифференциальных уравнении?

4. Чем отличается локальная ошибка от глобальной?

5. Какие из методов, явные или неявные, более устойчивы?

7