Сербо В. Г. Лекции по физике элементарных частиц

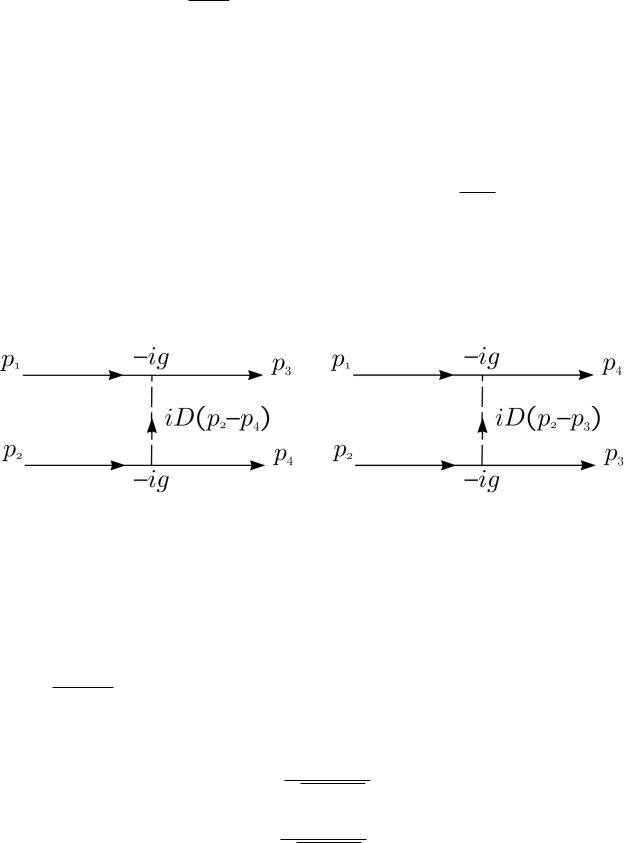
41

Введем новые переменные интегрирования:

	x + x0
X =	2 , z = x − x0, d4xd4x0 = d4Xd4z,

тогда

{. . .} = e−i(p1+p2−p3−p4)X e−i(p1−p3−p2+p4)z/2 + e−i(p1−p4−p2+p3)z/2 .

После интегрирования по X появится δ (p1 + p2 − p3 − p4). С учетом этого,

[. . .] = ei(p2−p4)z + ei(p2−p3)z

Обозначим через D(k) фурье-образ функции D(z):

Z D (z) eikzd4z = D (k) , D (z) = Z D (k) e−ikz d4k ,

(2π)4

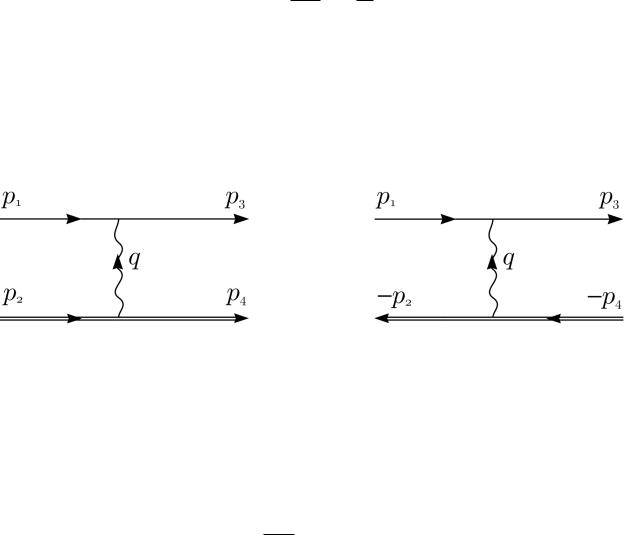
тогда амплитуда рассеяния процесса окажется выраженной через сумму двух пропагаторов в импульсном представлении (см. рис. 15 16)

iMf(2)i = (−ig)2 [iD (p2 − p4) + iD (p2 − p3)] .

Рис. 15. Рассеяние π−π− → π−π−:	Рис. 16. Рассеяние π−π− → π−π−:
t-обмен π0	u-обмен π0

В первой диаграмме аргумент пропагатора равен 4-импульсу промежуточной нейтральной частицы k = p2 − p4 = p3 − p1, òàê ÷òî k2 = t < 0. Эта диаграмма соответ-

ствует обмену π0 â t-канале; аналогично, вторая диаграмма соответствует обмену π0 â u-канале. В отличие от начальных и конечных частиц, для 4-импульсов которых справедливо равенство p2i = m2π−, i = 1 ÷ 4, для промежуточных частиц k2 6= m2π0 , а потому

p

εk = k2 + m2π0 6= k0 . Такие частицы называютсявиртуальными, а величина k2 − m2π0 называется виртуальностью данной промежуточной частицы. Виртуальность k2 −m2π0 характеризует отклонение частицы от массовой поверхности k2 = m2π0 . Виртуальная

частица живет время

τ p

1

|k2 − m2π0 |

и пролетает расстояние

1

r p .

|k2 − m2π0 |

42

Чем больше виртуальность, тем меньшие расстояния сможет прощупать такая частица см. глубоконеупругое рассеяние электрона на протоне (ср. опыты Резерфорда по исследованию структуры атома).

Аналогично можно рассмотреть процесс

π−π+ → π−π+ ,

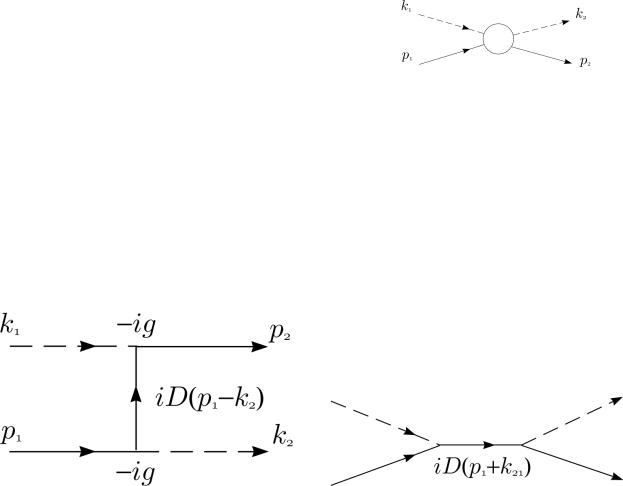
для которого амплитуда рассеяния равна (см. рис. 17 18)

iMf(2)i = (−ig)2 iD p0− − p− + iD (p− + p+) .

Рис. 17. Рассеяние π−π+ → π−π+:	Рис. 18. Рассеяние π−π+ → π−π+:
k2 < 0, t-обмен π0	k2 > 0, s-обмен π0

13.3. Пропагатор скалярной частицы

Используя свойства оператора	ˆ
	T
Tˆ hΦˆ (x) Φˆ	(x0)i =	ˆ	ˆ	(x0)
		Φˆ	(x0) Φˆ
		Φ (x) Φ (x )

представим пропагатор в виде

ïðè t > t0 ,

ïðè t0 > t

iD (x − x0) =	k,k0	1		2εk0V	hθ (t − t0) h0| cˆkcˆk+0	|0i e−ikx+ik0x0+
		√2εkV
	X
+	θ (t0 − t) h0| cˆk0cˆk+ |0i e−ik0x0+ikxi .

Здесь первое слагаемое в квадратных скобках соответствует процессу рождения промежуточного π0 в точке x0 и поглощение его в точке x, а второе слагаемое рождению

π0 в точке x и поглощению его в точке x0.

Ò.ê.

h0| cˆkcˆ+k0 |0i = δk,k0 ,

òî	1		X	1
						θ(t)e−iεkt+ikr + θ(−t)e+iεkt−ikr
	V
	iD(x) =		k	2εk			.

43 Теперь во втором слагаемом сделаем замену k → −k, перейд¼м от суммы по k ê

интегралу

→ Z

d3k

1

k

,

V

(2π)3

и окончательно получим

X

iD(x) = Z

3

d k

e−iεk|t|+ikr,

2εk(2π)3

ãäå |t| èç-çà θ(±t).

Покажем, что

∞

e−iεk|t|

Z

dk0

e−ik0t

= J , J = i

.

2εk

2π

k02 − εk2 + i0

−∞

Интеграл J легко бер¼тся по вычетам, полюса

подынтегрального выражения расположены в точ- ках (см. рис. 19)

±q

k −

±

Ðèñ.

19.

кость k0

k0 =

ε2

i0 =

εk

i0 .

Комплексная плос-

Åñëè t > 0, контур замыкаем в нижней полуплос-

кости:

1 e−iεkt

e−iεkt

J = i (−2πi)

=

,

2π 2εk

2εk

ч. т. д. Аналогично, при t < 0 контур замкн¼м в верхней полуплоскости:

J = i (+2πi)	1 eiεkt				=	e−iεk|t|	,
	2π (−2εk)
						2εk

ч. т. д. Итого:

D(x) = Z

d4k

e−ikx

, kx = k0t − kr, k0 6= εk = √

k2 + m2

, m ≡ mπ0 ,

(2π)4

k2 − m2 + i0

и потому в импульсном представлении

D(k) =

1

.

Òàê êàê

k2 − m2 + i0

pˆµpˆµ

− m2 D(x) = Z

d4k

k2 − m2

e−ikx

= δ(x),

(2π)4

k2 − m2 + i0

òî D(x) является функцией Грина уравнения КФГ. Явный вид D(x) дан в книге Боголюбова и Ширкова Ведение в теорию квантованных полей (Приложение 2) :

δ(λ)

m

im

θ(λ) hJ1

√m2λ − iN1 √m2λi −

√−m2λ ,

D(x) = −

+

8π√

4π2√

θ(−λ)K1

4π

λ

−λ

44

ãäå λ = x2 = t2 − r2, à J1(z), N1(z) è K1(z) функция Бесселя, функция Неймана и функция Ханкеля от мнимого аргумента. В окрестности светового конуса (при |λ|

1/m2):

D(x) = − 4π		+ 4π2		λ −		8π2 ln p
							2	|	| + 16π θ(λ).
	δ(λ)		i			im2	m2	λ			m2

Видно, что на световом конусе эта функция обладает целым букетом сингулярностей. Это означает, в частности, что в высших порядках теории возмущений, где будут встречаться произведение таких функций, придется специально доопределять эти плохо определ¼нные выражения (проблема бесконечностей). При |λ| 1/m2 пропагатор

быстро убывает, особенно в пространственно-подобной области:

			1			√
							m2	λ
					e−			|	|, ïðè λ < 0
D(x) =		|λ1|3/4
				,						ïðè λ > 0
		λ	3/4

13.4. Процесс π0π− → π0π− è π+π− → π0π0

Рассмотрим процесс (рис. 20)

π0π− → π0π− ,

для которого начальное и конечное состояние та-

êîâû:

i = aˆ1 cˆ1

0 ,

f

Рис. 20. Процесс π0π−

= aˆ2 cˆ2

0

.

π0π−

(13.1)

| i

+ +

| i

|

i

+ +

|

i

→

Матричный элемент этого процесса равен:

Sfi

=

−2!

Z

d4xd4x0 h0| cˆ2Tˆ Φ(ˆ

x)Φ(ˆ x0) cˆ1+ |0i ·

(2)

(

ig)2

h

i

+

(13.2)

h0| aˆ2Tˆ ϕˆ+(x)ϕˆ(x)ϕˆ+(x0)ϕˆ(x0) aˆ1

|0i .

В импульсном представлении в iMf(2)i дают вклад диаграммы, приведенные на ðèñ. 21 22:

Рис. 21. Диаграмма с π− обменом	Рис. 22. Диаграмма с π− обменом
â u-канале	â s-канале

45

Здесь D(p) фурье-образ пропагатора скалярной заряженной частицы D(x):

X0

V

V

0

ˆ

+

0

1

iD(x − x

) =

h0| T ϕˆ(x)ϕˆ (x

) |0i =

2εp 2εp0

·

ip0x0

ipx+ipp0 0

ˆ ˆ+

hθ (t − t0) h0| aˆpaˆp0 |0i e−

p,p

+ θ (t0

− t) h0| bp0bp |0i e−

i .

+

x

+ipx

Первое слагаемое в квадратных скобках соответствует частице, которая родилась в точке x0 и исчезла в точке x, второе слагаемое соответствует античастице, движущейся в

обратном направлении. Расч¼т D(x) для заряженной скалярной частицы не отличается от расч¼та для нейтральной скалярной частицы:

D(x) = Z	d4p e−ipx
	(2π)4 p2 − µ2 + i0 , µ ≡ mπ− .

Èòîã:	= −g2 (p1		− k2)2 − µ2	+ i0		+ (p1		+ k1)2 − µ2	+ i0
Mfi
(2)			1					1

Аналогично, процесс π−π+ → π0π0 определяется диаграммами, приведенными на рис. 23 24:

Рис. 23. Диаграмма с π− обменом		Рис. 24. Диаграмма с π− обменом
в t-канале	(p− − k1)2		+ (p− + k2)2	в u-канале
Mfi = −g2		− µ2		− µ2
(2)	1		1

14. Второй порядок теории возмущений в КЭД. Фотонный пропагатор

В операторе ˆ(2) упорядочение по времени можно производить отдельно для фотонных

S

и электрон-позитронных операторов, т. е.

		ie	2	Z
Sˆ(2)	=	(− )
		2!

h i h i

4 4 0 ˆ ˆ¯ ¯ 0 0 ˆ ˆµ ˆν 0

d xd x T Ψ(x)γµΨ(x)Ψ (x ) γνΨ (x ) T A (x)A (x ) .

рассеяния, который описы-

Ïðè ðàñ÷¼òå

46

14.1 Рассеяние электронов

При расч¼те сечения процесса e−e− → e−e− действуем по привычной схеме:

|ii	+ +	|0i ,		+ +	+	+	,
	= aˆ2 aˆ1			|fi = aˆ4 aˆ3	|0i , aˆi	≡ aˆpiσi
Sf(2)i = (−ie)2			Z	d4xd4x0iDµν (x − x0) fµν (x, x0) ,

ãäå

à

	1
fµν (x, x0) =	2! h0| aˆ3aˆ4Tˆ hΨ(¯ˆ x)γµΨ(x)Ψ¯ (x0) γνΨ (x0)i aˆ2+aˆ1+ |0i ,

h i

µν − 0 h | ˆ ˆµ ˆµ 0 | i iD (x x ) = 0 T A (x)A (x ) 0

пропагатор фотона

fµν будем действовать, как и в скалярном случае, учитывая дополнительно антикоммутативность фермионных операторов и спинорную структуру полей:

Ψ(ˆ x) = pσ	aˆpσupσ		2εp		+ . . .! , Ψ(¯ˆ x) = pσ	aˆp+σu¯pσ		2εp		+ . . .! .
X		e−ipx			X		e+ipx
		p					p
				V					V

Рис. 25. Вариант св¼рток в fµν	Рис. 26. Другой вариант св¼рток в
	fµν

fµν (x, x0) = 2!1 [ðèñ. 25 - ðèñ. 26 + (x ↔ x0)] =

= (¯u3γµu1) (¯u4γνu2) e−i(p1−p3)x−i(p2−p4)x0 − (¯u4γµu1) (¯u3γνu2) e−i(p1−p4)x−i(p2−p3)x0 .

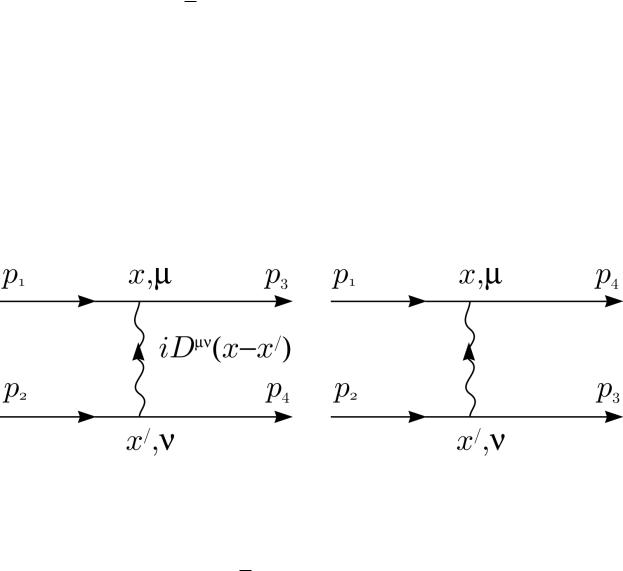
Дальнейшее интегрирование по x è x0 стандартно, итог (см. рис. 27 28):

iMf(2)i = (−ie)2 [(¯u3γµu1) iDµν (p3 − p1) (¯u4γνu2) − (¯u4γνu1) iDµν (p4 − p1) (¯u3γνu2)] .

Дополнительно: найти M(2) e−e+ → e−e+ fi для процесса

вается двумя диаграммами диаграммой рассеяния (фотон в t-канале) и диаграммой аннигиляции (фотон в s-канале).

47

Рис. 27. Диаграмма с γ обменом	Рис. 28. Диаграмма с	γ обменом
â t-канале	â u-канале

14.2. Фотонный пропагатор

Фотонный пропагатор уже определ¼н выше:

h i

µν − 0 h | ˆ ˆµ ˆν 0 | i iD (x x ) = 0 T A (x)A (x ) 0 .

Общий вид симметричного тензора второго ранга, зависящего от 4-вектора x, таков:

Dµν(x) = gµνD x2 − ∂µ∂νD(l) x2 ,

èëè â k-пространстве:

Dµν(k) = gµνD k2 + kµkνD(l) k2 ,

причем, в силу градиентной инвариантности, от D(l) (k2) физические результаты не должны зависеть. Поэтому достаточно найти D (k2) в любой калибровке. Мы будем

для расчета использовать кулоновскую калибровку, в которой ˆ

A0 = 0 è

X			V		−ikx	+	ikx
ˆ	√4π
A(x) =	√	2ωk		cˆkλekλ e		+ cˆkλekλ e		, kx = ωkt − kr.
kλ

Отличие от скалярного случая: общий множитель √4π, m = 0, ωk = |k| и наличие вектора поляризации ekλ. Ò. ê.

h0| cˆkλcˆ+k0λ0 |0i = δkk0δλλ0,

то, повторяя вычисления 13.3, получим

Dmn(x) = Z	d4k e−ikx				λ	(ekλ)m (ekλ)n ,
	(2π)4 k2 + i04π
					X

ãäå m, n = 1, 2, 3. Условие полноты векторов ekλ гласит

X	knkm
	(ekλ)m (ekλ)n = δmn −		, δmn = −gmn.
λ		k2

48

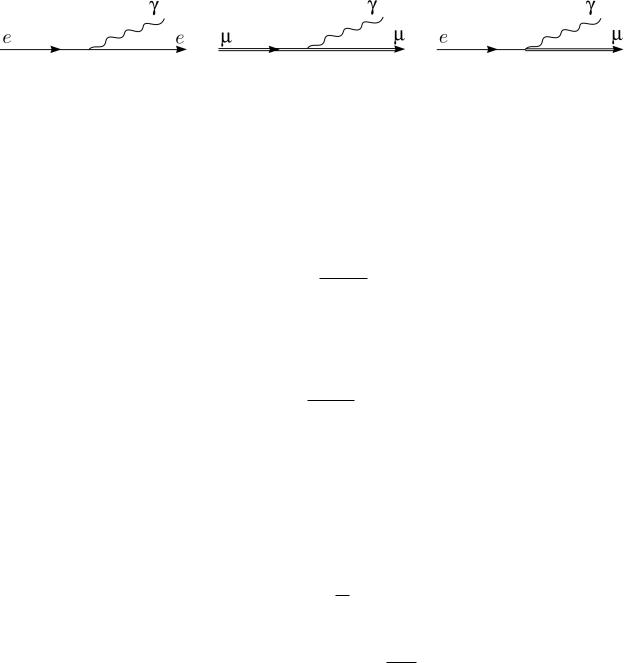
Рис. 29. Вершина e →

Рис. 30. Вершина µ →

Рис. 31. Вершина e →

eγ

µγ

µγ

Таком образом, в нашей калибровке

Dmn(k) = gmnD k2 + kmknD(l) k2 =

4π

δmn −

knkm

,

k2 + i0

k2

отсюда

D k2

4π

=

−

,

k2 + i0

Dµν k

4π

gµν

kµkνD(l)

k2

.

Часто выбирают D

(l)

2

(

) = k2−+ i0

+

(k

) = 0 (калибровка Фейнмана), тогда

Dµν(k) =

−4π

gµν .

k2 + i0

14.3. Диаграммы Фейнмана и закон Кулона

Рассмотрим рассеяние нерелятивистского электрона на мюоне

e−µ± → e−µ± .

Мюон может рассматриваться, как точечный источник кулоновского поля

U (r) = ±e2 , r

фурье-образ которого

Uq = Z U (r) e−iqrd3r = ±4qπe22 .

В квантовой механике дифференциальное сечение рассеяния

dσ			m		m	±	πe2	,
	= |f|2	, f = −	e	Uq = −	e		4
dΩ			2π		2π		q2

ãäå q = p0 − p è ε0 = ε.

В КЭД взаимодействие электромагнитного поля с e± è µ± описывается оператором

h

ˆ ˆα ˆ¯ ˆ

V (x) = eA (x) Ψe(x)γαΨe(x)

i

ˆ¯ ˆ

+ Ψµ(x)γαΨµ(x) ,

Таким образом в КЭД имеются элементарные вершины только двух типов рис. 29 и рис. 30, но нет вершин рис. 31.

49

Процесс e−µ− → e−µ− описывается одной диаграммой (рис. 32):

iMfi = (−ie)2 (¯u3γαu1) iDαβ(q) (¯u4γβu2) .

В системе покоя начального µ− (эта система для нерелятивистского e− совпадает с ÑÖÈ, ò. ê. mµ ≈ 200 me)

q = p3 − p1 = (0, q) , q2 = −q2 ,

все биспиноры uj имеют только верхние компоненты, потому (¯u3γαu1) 6= 0 только при α = 0, (¯u4γβu2) 6= 0 только при β = 0 è

D00 = −4π = +4π .

q2 q2

В итоге:

4πe2

u3+u1 u4+u2

4πe2

Mfi = −

= −

2meδσ1σ3 2mµδσ2σ4 .

Ó÷òÿ, ÷òî

q2

q2

dΩ = |f|2

=

8π (mµ + me)

2

èëè f = 8πmµ ,

dσ

Mfi

Mfi

получим согласие с результатом из квантовой механики.

Рис. 32. Процесс e−µ− → e−µ−

Рис. 33. Процесс e−µ+ → e−µ+

Для процесса e−µ+ → e−µ+ амплитуда рассеяния (см. рис. 33)

iMfi = (−1) (−ie)2 (¯u3γαu1) iDαβ(q) (¯v2γβv4) ,

где дополнительный множитель (−1) связан с антикоммутативностью фермионных операторов и другим набором св¼рток для µ+, ÷åì äëÿ µ−. В итоге

4πe2

Mfi = + q2 2meδσ1σ3 2mµδσ2σ4 .

Таким образом, закон Кулона, соответствующий силам отталкивания для e−µ− è силам притяжения для e−µ+, связан с обменом векторной частицей фотоном между

заряженными фермионами. Покажите, что для взаимодействия

h i

ˆ ˆ ˆ¯ ˆ ˆ¯ ˆ

V (x) = gΦ(x) Ψe(x)Ψe(x) + Ψµ(x)Ψµ(x)

50

амплитуда e−µ± → e−µ± рассеяния определяется обменом нейтральной скалярной ча-
стицей и равна			g2
Mfi =					2meδσ1σ3 2mµδσ2σ4 ,
			+ m2
	q2
что соответствует потенциальной энергии вида
Uq = −		g2		, U(r) = −		g2	/4π	e−rm,
	q2 + m2						r

т. е. юкавскому потенциалу притяжения как для e−µ−, òàê è äëÿ e−µ+ взаимодействия.

14.4. Процесс аннигиляции e+e− → µ+µ−

Для этого процесса закон сохранения 4- импульса имеет вид

p1 + p2 = p3 + p4 ,

а переменные Мандельстама таковы

s = (p1 + p2)2 , t = (p1 − p3)2 ,

u = (p1 − p4)2 ,

Ðèñ.

34. Процесс e+e− →

ïðè ýòîì

µ+µ−

s + t + u = 2m2 + 2µ2 , p12 = p22 = m2 , p32 = p42 = µ2 ,

а также

p1p3 = p2p4, p1p4 = p2p3 .

Амплитуда рассеяния

M

= (

−

ie)2

(¯v

γ

u

)

−4πgαβ

(¯u

γ v

) =

4πα

F ,

s

fi

1

α

2

4

β 3

s

ãäå

F = (¯v1γαu2) (¯u4γαv3) .

Искомое сечение для неполяризованных частиц содержит

1 1

σX1,2,3,4

|F |2 =

1Sp

(6p1 − m) γα (6p2 + m) γβ

1

Sp {(6p4 + µ) γα

(6p3 − µ) γβ} =

2

2

2

2

=

n2p1 p2

2+ 2p2 p1

− 2

o {223α

4β2+ 2 4α

3β −

αβ} =

α β

α β

sgαβ

p p

p p

sg

= 8 (p1p3) + 8 (p1p4) + 4s µ + m ,

ãäå 6p ≡ pαγα.

 ñ.ö.è.

p1p3 = ε21 (1 − vevµ cos θ) , p1p4 = ε21 (1 + vevµ cos θ) ,

ãäå θ угол между p1 è p3 (угол вылета e+), а скорости электрона и мюона равны

ve = r	1 −	4 s
		m2

µ+ по отношению к направлению движения

, vµ = r
	1 −	4s .
		µ2