2.4.4. Операции реляционной алгебры

Операндами для операций реляционной алгебры являются реляционные отношения. Результатом выполнения операций РА также является отношение. Таким образом, механизм реляционной алгебры замкнут относительно понятия отношения. Это позволяет применять операции РА каскадно.

Использование операций РА накладывает на отношения два ограничения:

• порядок столбцов (полей) в отношении фиксирован;

• отношения конечны.

Существует пять основных операций реляционной алгебры – проекция, селекция, декартово произведение, разность, объединение, – и три вспомога-тельных: соединение, пересечение и деление. Вспомогательные операции могут быть выражены через основные, но в некоторых системах реализуются с помощью специальных команд (ключевых слов) для удобства пользователей.

1. Проекция (projection)

Это унарная операция (выполняемая над одним отношением), служащая для выбора подмножества атрибутов из отношения R. Она уменьшает арность отношения и может уменьшить мощность отношения за счёт исключения одинаковых кортежей.

Пример 1. Пусть имеется отношение R(A,B,C) (рис. 2.10,а).

Тогда проекция _A,C(R) будет такой, как показано на рис. 2.10,б.

Отношение R
A	B	C
a	b	c
c	a	d
c	b	d
a)

Секция AC(R)
A	C
a	c
c	d
б)

Рис.2.10. Пример проекции отношения

2. Селекция (selection)

Это унарная операция, результатом которой является подмножество кортежей исходного отношения, соответствующих условиям, которые накладываются на значения определённых атрибутов.

Пример 2. Для отношения R(A,B,C) (рис. 2.11,а) селекция _C=d(R) (при условии "значение атрибута C равно d") будет такой (рис. 2.11,б):

Отношение R
A	B	C
a	b	c
c	a	d
c	b	d
a)

Секция C=d(R)
A	B	C
c	a	d
c	b	d
б)

Рис. 2.11. Пример селекции отношения

3. Декартово произведение (Cartesian product)

Это бинарная операция над разносхемными отношениями, соответст-вующая определению декартова произведения для РМД.

Пример 3. Пусть имеются отношение R(A,B) и отношение S(C,D,E) (рис. 2.12,а). Тогда декартово произведение R×S будет таким (рис. 2.12,б).

Отношение R

A
Ba	b
c	a
b	d

Отношение S
C	D	E
1	2	3
4	5	6

Декартово произведение R ×S
A	B	C	D	E
a	b	1	2	3
a	b	4	5	6
c	a	1	2	3
c	a	4	5	6
b	d	1	2	3
b	d	4	5	6

a)

б)

Рис. 2.12. Пример декартова произведения отношений

4. Объединение (union).

Объединением двух односхемных отношений R и S называется отношение T = R ∪ S, которое включает в себя все кортежи обоих отношений без повторов.

5. Разность (minus).

Разностью односхемных отношений R и S называется множество кортежей R, не входящих в S.

Пример 4. Пусть имеются отношение R(A,B,C) и отношение S(A,B,C) (рис. 2.13,а). Тогда разность R–S будет такой (рис. 2.13,б):

Отношение R

A
aBC	b	c
c	a	d
c	h	c

Отношение S
A	B	C
g	h	a
h	d	d

Разность R–S
A	B	C
c	a	d
c	h	c

a)

б)

Рис. 2.13. Пример разности отношений

Следующие три операции являются вспомогательными операциями РА.

6. Пересечение (intersection).

Пересечение двух односхемных отношений R и S есть подмножество кортежей, принадлежащих обоим отношениям. Это можно выразить через разность:

R∩S=R - (R-S))

7. Соединение (join).

Эта операция определяет подмножество декартова произведения двух разносхемных отношений. Кортеж декартова произведения входит в результирующее отношение, если для атрибутов разных исходных отноше-ний выполняется некоторое условие F. Соединение может быть выражено так:

RS=_F(R×S))      F

Если условием является равенство атрибутов исходных отношений, такая операция называется эквисоединением. Естественное соединение – это эквисоединение по одинаковым атрибутам исходных отношений.

Пример 5. Пусть имеются отношения R(A,B,C) и S(A,D,E) (рис. 2.14,а). Тогда естественное соединение R  S будет таким, как показано на рис. 2.14,б.

Отношение R

A
aBC	b	c
c	a	d
c	h	c
g	b	d

Отношение S
A	D	E
g	h	a
c	b	c
h	d	d

Соединение RS
A	B	C	D	E
c	a	d	b	c
c	h	c	b	c
g	b	d	h	a

a)

б)

Рис. 2.14. Пример естественного соединения отношений

8. Деление (division).

Пусть отношение R содержит атрибуты {r₁,r₂,...,r_k, r_k+1,...,r_n}, а отношение S – атрибуты {r_k+1,...,r_n}. Тогда результирующее отношение содержит атрибуты {r₁,r₂,...,r_k}. Кортеж отношения R включается в результирующее отношение, если его декартово произведение с отношением S входит в R

Пример 6. Пусть имеются отношения R(A,B,C) и S(A,B) (рис. 2.15,а). Тогда частное R/S будет таким как показано на рис. 2.15,б.

Отношение R

DA
aBC	b	c	b
c	f	g	h
a	v	c	b
a	b	g	h
c	v	g	h
c	f	c	b

Отношение S
C	D
g	h
c	b

Частное R/S
A	B
a	b
c	f

a)

б)

Рис. 2.15. Пример операции деления

Языком обработки данных, основанным на реляционной алгебре, является SQL (основы этого языка изложены в [3]).

10. Понятие функциональной зависимости. Способ определения функциональных зависимостей. Замыкание множества зависимостей. Аксиомы Армстронга. Замыкание множества атрибутов. Неприводимое множество функциональных зависимостей.

3.1.1. Понятие функциональной зависимости

 

Вспомним, что любое отношение рассматривается как переменная, принимающая определенные значения в определенные моменты времени.

Пусть R – переменная отношения, X, Y – произвольные подмножества множества всех атрибутов R. Y функционально зависит от Xтогда и только тогда, когда для любого допустимого значения R каждое значение X связано только с одним значением Y.

Обозначается: X→Y

Говорится: «X функционально определяет Y» или «Y функционально зависит от X».

Левая часть выражения называется детерминантом (детерминантой) функциональной зависимости (ФЗ), правая – зависимой частьюФЗ.

 

Например, в отношении Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Адрес, КодГруппы) существуют такие ФЗ

               {№ ЗачетнойКнижки} → {Фамилия, Имя, Отчество}

               {№ ЗачетнойКнижки} → {Адрес, КодГруппы}

               {№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес, КодГруппы}

Это лишь некоторые ФЗ, из которых можно сделать вывод, что если детерминант содержит первичный ключ, то множество всех остальных атрибутов отношения функционально зависит от него.

Еще пример: в отношении Кафедры (КодКафедры, НазваниеКафедры, Кабинет, Телефон) существуют ФЗ

               {КодКафедры} → {Кабинет, Телефон}

               {НазваниеКафедры} → {Кабинет, Телефон}

Таким образом, аналогичный вывод можно сделать не только для первичных ключей, но и для альтернативных, то есть для всех потенциальных ключей.

 

Множество атрибутов отношения, которое содержит в качестве подмножества потенциальный ключ называется суперключом этого отношения.

 

Рассмотрим еще один пример: если в то же отношение Студенты добавить атрибут СтаростаГруппы, то появятся такие ФЗ:

               {КодГруппы} → {СтаростаГруппы}

               {СтаростаГруппы} → {КодГруппы}

(причем, ни атрибут КодГруппы, ни атрибут СтаростаГруппы не являются потенциальными ключами)

В этом случае имеется избыточность данных, которая может привести к вводу ошибочных сведений (пользователь случайно может ввести в качестве старосты некоторой группы не того студента, который на самом деле является старостой, но система не выдаст ошибку).

 

Фактически, если в отношении имеется ФЗ, в которой детерминант не является суперключом, то отношение избыточно.

 

Существуют такие ФЗ, которые учитываются только формально, т.к. они всегда существуют и подразумеваются самим определением ФЗ. Это тривиальные ФЗ.

Тривиальная функциональная зависимость– это такая ФЗ, зависимая часть которой является подмножеством детерминанта.

 

Например,

               {№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Фамилия, Имя, Отчество}

               {КодГруппы, Курс} → {Курс}

Такие тривиальные ФЗ не рассматриваются при нормализации, но все же они существуют и всегда формально учитываются.

 

3.1.2. Правила вывода функциональных зависимостей (может, этот п. не надо?)

 

Из некоторого множества ФЗ конкретного отношения можно получить производные ФЗ.

Например, из ФЗ отношения Студенты

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес, Телефон}

можно получить такие ФЗ:

               {№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес}

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Телефон}

 

Пусть S – некое множество ФЗ. Тогда множество всех ФЗ, которые можно получить из S называется замыканием множества S и обозначается S⁺.

 

Чтобы получить замыкание некоторого множества ФЗ нужны правила вывода ФЗ. Такие правила вывода сформулировал Армстронг (Швеция), поэтому их называют правилами Армстронга (или аксиомами Армстронга).

Обозначим за А, В, С произвольные подмножества множества атрибутов заданного отношения R, а записью АВ будем обозначать объединение А и В.

Правила вывода ФЗ Армстронга:

1)      Рефлексивность:   если В является подмножеством А, то А → В

2)      Дополнение:          если А → В, то АС → ВС

3)      Транзитивность:    если А → В и В → С, то А → С

Каждое из этих правил может быть доказано на основе определения ФЗ, а первое правило – это определение тривиальной ФЗ.

Эти правила полны, т.к. их достаточно для вывода замыкания (т.е. всех ФЗ) начального множества ФЗ.

Они также исчерпывающи, т.к. никакие дополнительные ФЗ не могут быть выведены из начального множества ФЗ.

 

Но из этих правил для упрощения практического вывода ФЗ можно вывести несколько дополнительных правил (следствий):

4)      Самоопределение:            А → А

5)      Декомпозиция:      если А → ВС, то А → В и А → С

6)      Объединение:        если А → В и А → С, то А → ВС

7)      Композиция:          если А → В и С → D, то АС → ВD

8)      Теорема всеобщего объединения: если А → В и С → D, то А(С-В) → ВD

(названо это правило так, потому что многие другие правила могут быть выведены как частные случаи этой теоремы)

 

Пример: рассмотрим отношение Группы (КодГруппы, Специальность, Курс, Староста).

В качестве начального множества ФЗ возьмем множество из следующих двух ФЗ:

               (1) {КодГруппы} → {Специальность, Курс}

               (2) {КодГруппы} → {Староста}

Выведем замыкание этого множества ФЗ.

         По правилу 1 можно записать все тривиальные зависимости:

               (3) {Специальность, Курс} → {Специальность}

               (4) {Специальность, Курс} → {Курс}

         По правилу 2:

               (5) {КодГруппы, Староста} → {Специальность, Курс, Староста}

               (6) {КодГруппы, Специальность} → {Староста, Специальность}

               (7) {КодГруппы, Курс} → {Староста, Курс}

               (8) {КодГруппы, Специальность, Курс} → {Староста, Специальность, Курс}

         По правилу 3 напрямую ничего не выведем.

         По правилу 4:

               (9) {КодГруппы} → {КодГруппы}

               (10) {Специальность} → {Специальность}

               и т.д. (11), (12)

         По правилу 5:

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

         По правилу 6:

(15) {КодГруппы} → {Специальность, Курс, Староста}

         По правилу 7 напрямую ничего не выведем

         По правилу 8 тоже.

 

Однако, знание этих правил и умение ими пользоваться не обеспечивают вывода замыкания множества ФЗ, т.к. не существует четкого алгоритма такого вывода.

 

3.1.3. Неприводимые функциональные зависимости

 

Функциональная зависимость называется неприводимой слева, если ни один атрибут не может быть опущен из ее детерминанта без нарушения зависимости (иными словами, детерминант неизбыточен).

 

Например: ФЗ {№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес} приводима, т.к. из детерминанта можно исключить атрибутыФамилия, Имя, Отчество без нарушения ФЗ.

А ФЗ {КодГруппы, Дисциплина} → {Преподаватель} отношения Занятия (КодГруппы, Дисциплина, Преподаватель) неприводима, т.к. из детерминанта нельзя исключить ни атрибут КодГруппы, ни атрибут Дисциплина без нарушения зависимости.

 

Множество ФЗ называется неприводимым тогда и только тогда, когда выполняются три свойства:

1)         зависимая часть каждой ФЗ из данного множества содержит только один атрибут;

2)         каждая ФЗ из данного множества является неприводимой слева;

3)         ни одна ФЗ из данного множества не может быть опущена.

 

Например, рассмотрим множество ФЗ отношения Группы из примера в предыдущем п.3.1.2.

               (1) {КодГруппы} → {Специальность, Курс}

               (2) {КодГруппы} → {Староста}

               (3) {Специальность, Курс} → {Специальность}

               (4) {Специальность, Курс} → {Курс}

               (5) {КодГруппы, Староста} → {Специальность, Курс, Староста}

               (6) {КодГруппы, Специальность} → {Староста, Специальность}

               (7) {КодГруппы, Курс} → {Староста, Курс}

               (8) {КодГруппы, Специальность, Курс} → {Староста, Специальность, Курс}

               (9) {КодГруппы} → {КодГруппы}

               (10) {Специальность} → {Специальность}

               (11) {Курс} → {Курс}

               (12) {Староста} → {Староста}

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

(15) {КодГруппы} → {Специальность, Курс, Староста}

 

По первому свойству исключаем из этого множества следующие ФЗ: (1), (5), (6), (7), (8), (15).

По второму свойству исключаем следующие ФЗ: (3), (4).

По третьему свойству исключаем: (9), (10), (11), (12).

Остались:

               (2) {КодГруппы} → {Староста}

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

 

Полученное множество ФЗ неприводимо. Можно сделать вывод, что полученное множество ФЗ выражает то, что отношение Группысодержит атрибуты КодГруппы, Староста, Специальность, Курс, и КодГруппы – первичный ключ.

 

3.1.4. Диаграммы (схемы) функциональных зависимостей (может, этот п. не надо?)

 

Множество неприводимых ФЗ некоторого отношения можно представить в виде диаграммы функциональных зависимостей.

Из таких диаграмм лучше видно, какие ФЗ включить в множество ФЗ, а какие исключить, чтобы оно было неприводимо. Исключить нужно те стрелки (обозначающие ФЗ), которые идут не от потенциального ключа.

Таким образом, с помощью диаграмм можно привести множество ФЗ к неприводимому состоянию.

В качестве примера рассмотрим диаграмму первоначального множества ФЗ из п. 3.1.2.

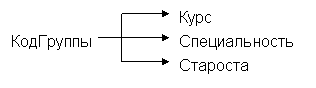
После того, как лишние стрелки будут убраны, получим диаграмму:

Из нее как раз и следуют перечисленные ранее три оставшиеся ФЗ:

                                   {КодГруппы} → {Курс}

                                   {КодГруппы} → {Специальность}

                                   {КодГруппы} → {Староста}

 

Таким образом, существует как минимум два способа преобразования множества ФЗ к неприводимому состоянию - путем проверки всех свойств их определения и путем анализа диаграмм ФЗ.

 

11. Нормализация. Декомпозиция отношений без потерь. Первая нормальная форма – 1НФ. Вторая нормальная форма – 2НФ. Третья нормальная форма – 3НФ. Аномалии включения, удаления, обновления. Определение максимально нормальной формы переменной – отношения по заданному неприводимому множеству функциональных зависимостей.

Сначала будет рассмотрен классический подход, при котором весь процесс проектирования производится в терминах реляционной модели данных методом последовательных приближений к удовлетворительному набору схем отношений. Исходной точкой является представление предметной области в виде одного или нескольких отношений, и на каждом шаге проектирования производится некоторый набор схем отношений, обладающих лучшими свойствами. Процесс проектирования представляет собой процесс нормализации схем отношений, причем каждая следующая нормальная форма обладает свойствами лучшими, чем предыдущая.

Каждой нормальной форме соответствует некоторый определенный набор ограничений, и отношение находится в некоторой нормальной форме, если удовлетворяет свойственному ей набору ограничений. Примером набора ограничений является ограничение первой нормальной формы - значения всех атрибутов отношения атомарны. Поскольку требование первой нормальной формы является базовым требованием классической реляционной модели данных, мы будем считать, что исходный набор отношений уже соответствует этому требованию.

В теории реляционных баз данных обычно выделяется следующая последовательность нормальных форм:

• первая нормальная форма (1NF);

• вторая нормальная форма (2NF);

• третья нормальная форма (3NF);

• нормальная форма Бойса-Кодда (BCNF);

• четвертая нормальная форма (4NF);

• пятая нормальная форма, или нормальная форма проекции-соединения (5NF или PJ/NF).

Основные свойства нормальных форм:

• каждая следующая нормальная форма в некотором смысле лучше предыдущей;

• при переходе к следующей нормальной форме свойства предыдущих нормальных свойств сохраняются.

В основе процесса проектирования лежит метод нормализации, декомпозиция отношения, находящегося в предыдущей нормальной форме, в два или более отношения, удовлетворяющих требованиям следующей нормальной формы.

Наиболее важные на практике нормальные формы отношений основываются на фундаментальном в теории реляционных баз данных понятии функциональной зависимости. Для дальнейшего изложения нам потребуются несколько определений.

Определение 1. Функциональная зависимость

В отношении R атрибут Y функционально зависит от атрибута X (X и Y могут быть составными) в том и только в том случае, если каждому значению X соответствует в точности одно значение Y: R.X (r) R.Y.

Определение 2. Полная функциональная зависимость

Функциональная зависимость R.X (r) R.Y называется полной, если атрибут Y не зависит функционально от любого точного подмножества X.

Определение 3. Транзитивная функциональная зависимость

Функциональная зависимость R.X -> R.Y называется транзитивной, если существует такой атрибут Z, что имеются функциональные зависимости R.X -> R.Z и R.Z -> R.Y и отсутствует функциональная зависимость R.Z --> R.X. (При отсутствии последнего требования мы имели бы "неинтересные" транзитивные зависимости в любом отношении, обладающем несколькими ключами.)

Определение 4. Неключевой атрибут

Неключевым атрибутом называется любой атрибут отношения, не входящий в состав первичного ключа (в частности, первичного).

Определение 5. Взаимно независимые атрибуты

Два или более атрибута взаимно независимы, если ни один из этих атрибутов не является функционально зависимым от других.