
3
.doc17.
3.11. Производная функции, заданной параметрически.
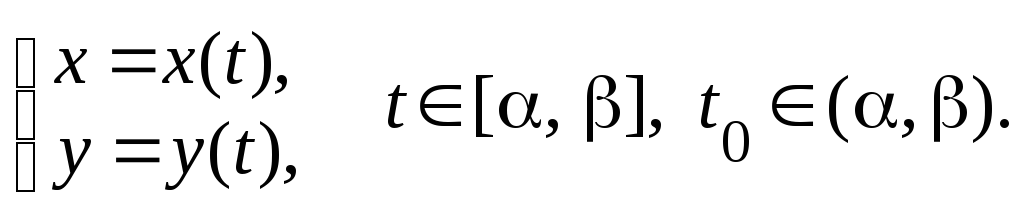 Пусть
x(t),
y(t)
имеют непрерывные производные в
окрестности точки t0
и при этом x(t0)
0.
на некотором интервале оси t,
содержащем точку t0,
функция x(t)
монотонна, имеет обратную функцию
определена дифференцируемая сложная
функция y(t(x))(будем
обозначать ее просто y(x)).
В
явном виде эту зависимость найти часто
не удается, научимся находить производную
функции y(x)
через заданные в условии зависимости
x(t),
y(t).
Пусть
x(t),
y(t)
имеют непрерывные производные в
окрестности точки t0
и при этом x(t0)
0.
на некотором интервале оси t,
содержащем точку t0,
функция x(t)
монотонна, имеет обратную функцию
определена дифференцируемая сложная
функция y(t(x))(будем
обозначать ее просто y(x)).
В
явном виде эту зависимость найти часто
не удается, научимся находить производную
функции y(x)
через заданные в условии зависимости
x(t),
y(t).
Используем свойство
инвариантности формы дифференциала
относительно функциональных подстановок.![]()
Замечание.
Формула
не дает явной зависимости производной
от переменной x,
будет известна только зависимость ее
от t.
Поэтому удобнее применять другие
обозначения:![]() ,
,
![]()
Пример. Найти производную функции y(x) в точке, соответствующей заданному значению параметра:
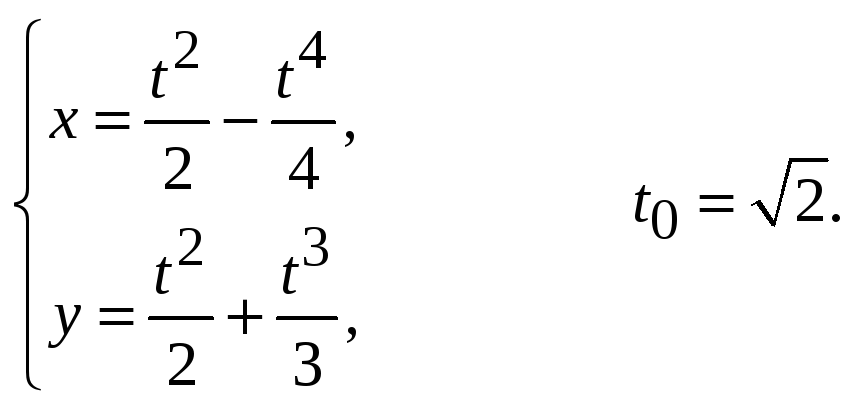 Решение.
y(t).=
(t
+ t2),
x(t)
= (t
– t3),
Решение.
y(t).=
(t
+ t2),
x(t)
= (t
– t3),![]()
Найдем
x0
= x(t0)
= 0, y0
= y(t0)
=
![]() ,
,
![]()
Касательная y
= y0
+ y(x0)(x
– x0):
![]()
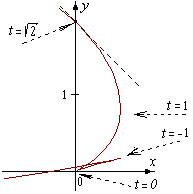 Обратим
внимание на то, что кривая имеет острые
изломы в точках, соответствующих
значениям t
= –1 и t
= 0. В этих
точках одновременно меняется вид
монотонности функций x(t),
y(t).
Такие точки называют точками
возврата
кривой, в них одновременно x(t)
= 0, y(t)
= 0.
Обратим
внимание на то, что кривая имеет острые
изломы в точках, соответствующих
значениям t
= –1 и t
= 0. В этих
точках одновременно меняется вид
монотонности функций x(t),
y(t).
Такие точки называют точками
возврата
кривой, в них одновременно x(t)
= 0, y(t)
= 0.
Определение
гладкой кривой.
Кривая
![]() называется
гладкой,
если x(t),
y(t)
имеют непрерывные производные и (xt)2
+ (yt)2
≠ 0.
Изменению параметра
t
на отрезке [,
]
взаимно однозначно соответствует
движение точки по кривой от A(x(),
y())
к B(x(),
y())
и нет точек возврата. В каждой точке
такой кривой при t(,
)
существует касательная, угловой
коэффициент которой
называется
гладкой,
если x(t),
y(t)
имеют непрерывные производные и (xt)2
+ (yt)2
≠ 0.
Изменению параметра
t
на отрезке [,
]
взаимно однозначно соответствует
движение точки по кривой от A(x(),
y())
к B(x(),
y())
и нет точек возврата. В каждой точке
такой кривой при t(,
)
существует касательная, угловой
коэффициент которой
![]() (или
(или
![]() )
в окрестности
этой точки меняется
непрерывно. Кривая, являющаяся
объединением конечного числа гладких
кривых, называется
кусочно-гладкой
кривой.
)
в окрестности
этой точки меняется
непрерывно. Кривая, являющаяся
объединением конечного числа гладких
кривых, называется
кусочно-гладкой
кривой.
