Акулов, Федотов. Основы теории биотехнических систем

вая интенсивность стимула. Физико-химические процессы образования медиаторов нейромышечной передачи в этой модели не описываются.

Структурная идентификация дает возможность установить, как взаимодействуют отдельные компоненты объекта в процессе формирования его поведения. Структурная идентификация связана с изучением механизмов функционирования, способов организации и внутреннего строения биологических звеньев БТС. Одним из возможных путей исследования структурной организации биологических звеньев является анатомическое, физиологическое изучение объекта, представление его в виде отдельных составляющих, описание биофизических и биохимических механизмов функционирования этих составляющих.

В отдельных случаях, механизм функционирования исследуемого объекта предполагается известным. Тогда возникает возможность сделать предположение о классе функционального описания поведения объекта (в виде уравнения модели, параметры которого остаются неизвестными). В этом случае задача идентификации объекта сводится к задаче оценивания параметров уравнения модели.

Функциональная идентификация предусматривает определение передаточной функции объекта, не давая информации о внутреннем строении. Однако, по мере того, как становится возможным наблюдение большего числа переменных, описывающих состояние объекта, могут выявляться скрытые ранее компоненты. Объект может быть разбит на части, т.е. может быть произведена декомпозиция “черного ящика”. Таким образом, возможно чередование функциональной и структурной идентификации объекта.

Функциональная идентификация может быть реализована с помощью методов, основанных на тестировании объекта с помощью сигналов, позволяющих определить его передаточную функцию. В качестве тестирующих сигналов используются синусоидальное, ступенчатое, импульсное или шумовое воздействие.

60

Обработка реакций, вызванных тест-воздействием, с помощью методов, основанных на преобразовании Фурье, позволяет найти частотную характеристику, далее передаточную функцию объекта и перейти к описанию поведения объекта в виде дифференциальных уравнений.

Метод пространства состояний позволяет представить мо-

дель, описываемую передаточной функцией, в виде системы дифференциальных уравнений первой степени, часто имеющих вполне определенный биофизический смысл. Интерпретация этих уравнений с помощью камерных моделей позволяет в ряде случаев от моделирования биологических объектов перейти к структурному моделированию, характеризующему механизмы происходящих процессов.

Численные параметрические методы идентификации являются поисковыми методами, с помощью которых путем перебора значений параметров можно определить модель объекта, описывающую взаимодействие атрибутов. К данным методам относятся методы инвариантного погружения, последовательного обучения, а также эвристические методы идентификации.

Таким образом, результатом идентификации биологических звеньев БТС является получение описания их функционирования в виде совместимом с описанием технических звеньев для формирования модели БТС в целом.

2.2.Методы оценки параметров модели

Вцелом ряде случаев идентификации биологических объектов, рассматриваемых в качестве звеньев БТС, считается известным вид функциональной связи выходных и входных атрибутов моделируемого объекта. Тогда экспериментальные данные, полученные в результате исследования объекта, могут быть непосредственно использованы для задания его формального описания. В случае статических систем для отыскания математической модели

вформе функциональной зависимости, “наилучшим” образом удовлетворяющей экспериментальным данным, может использоваться

61

регрессионный анализ. Для моделирования динамических систем, когда известным считается механизм процесса и дифференциальное уравнение, его описывающее, задача сводится к определению параметров данного уравнения.

Статическая задача оценивания параметров модели сводится к выбору вида функциональной зависимости, описывающей экспериментальные данные, и ее аналитического описания, т.е. к подбору функции и определению ее параметров. В регрессионном анализе для моделирования используются степенные, показательные, дробно-рациональные функции. Выбор вида функции может быть обусловлен известным характером исследуемого процесса, известными механизмами функционирования системы.

Критерий “наилучшего” описания системы с помощью выбранной функциональной зависимости состоит в минимизации отклонений математической модели от экспериментальных данных. Для этой цели может быть использован ряд методов, среди которых наиболее часто применяется метод наименьших квадратов. Данный метод заключается в нахождении значений параметров модели, минимизирующих сумму квадратов отклонений экспериментальных данных от соответствующих значений выбранной функции.

В случае однофакторного анализа (одна независимая переменная в задании системы), экспериментальные данные, связывающие вход и выход системы можно представить в виде:

{xi , yi }

(2.1)

где: x – входные данные; y – выходные данные; i = 1…n, здесь n – количество экспериментальных точек.

Аппроксимирующая функция может быть записана в виде:

y = f (x,{aK })	(2.2)

где: {aK } – параметры функции.

Тогда отклонения экспериментальных данных от соответствующих значений модели записываются в виде:

62

	(2.3)
yi = yi − yi
где: yi = f (xi{aк}).
Условие реализации метода наименьших квадратов:
n
∑ yi2 → min	(2.4)

i=1

Минимизация суммы квадратов отклонений может быть реализована с помощью машинных алгоритмов или в аналитическом случае решением системы уравнений для параметров аппроксимирующей функции:

d		n		2
		∑	y	i		= 0	(2.5)
daК i=1

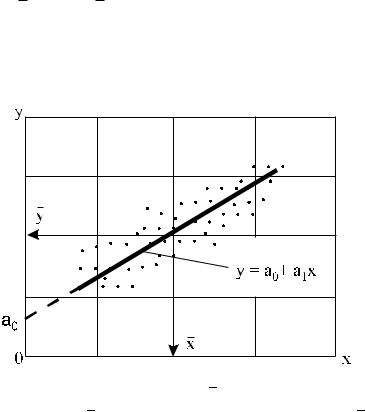
Рассмотрим формирование модели, описывающей связь экспериментально полученных данных значений максимальной величины ЧСС, при пробе с нарастающей физической нагрузкой, от возраста обследуемого. Целью моделирования является определение зависимости, необходимой для разработки алгоритма диагностического устройства системы. Графическое представление данных в координатах атрибутов системы (у – ЧСС, х – возраст) показывает, что для модели можно воспользоваться линейной регрессией (рисунок 2.2):

	+ a1x	(2.6)
y = a0

Для случая линейной регрессии уравнения (2.5) имеют простое решение. Действительно:

n

∑ yi2 = ∑( yi − a0 − a1xi )2

1

dad0 [∑ yi2 ]= −2∑(yi − a0 − a1xi )= 0 dad1 [∑ yi2 ]= −2∑(yi − a0 − a1xi )xi = 0

63

+ a1

∑xi = ∑ yi

a0n

(2.7)

∑

+ a1

∑

xi2 =

∑

a0

xi

xi yi

Поделив первое уравнение на n, получим:

a0 + a1x = y

(2.8)

где: x = 1 n

x ,

y = 1

n

y

i

– средние значения переменных.

n ∑1

i

n ∑1

Таким образом, первое уравнение системы (2.7) требует, что-

бы аппроксимирующая функция (прямая) проходила через “центр

тяжести” множества экспериментальных точек, имеющего коор-

динаты (x, y ).

Рисунок 2.2 – Линейная регрессия экспериментальных данных

Если центрировать уравнения по x ,

т.е. перенести начало ко-

ординат в точку

[x; 0

], то в новых координатах [x′ = x − x; y]

можно получить значения параметров a′, a′ уравнения регрессии:

1

0

При x = 0 ,

уравнение

(2.8)

дает a′ = y , второе уравнение

системы (2.7) при x′ = 0 , дает:

0

64

a′	=	∑x′yi	(2.9)
1		∑xi′xi′

Таким образом, получаем величину угла наклона прямой регрессии. Уравнение регрессии в новых координатах принимает

вид:
	= a′			+ a′x′	;
y
		0		1
y	= y + a′x′ ;
				1
y = a′x + a′x .
	1			1
Или:
y	= y + a′(x − x)= xx ;
				1
a	= (y − a′x);
0				1
a = a′ .
1	1

Для рассматриваемого примера раздела 1.1 в соответствии с таблицей 1.1, где приведены данные обследования, показывающие величину максимальной ЧСС при физической нагрузке в зависимости от возраста обследуемых, имеем: x = 45 [лет]; y = 178,4

[уд/мин]. С учетом (2.8) и (2.9):

y = 216 − 0,83x2	(2.10)
Метод наименьших квадратов дает	правильные результаты

при однородной статистике, т.е. статистике отфильтрованной от промахов. Поэтому перед использованием метода данные экспериментов необходимо сглаживать, например, обрабатывать медианным фильтром.

Регрессионный анализ решает статическую задачу представления экспериментальных данных в виде математической модели. Рассмотрение динамической задачи возможно, если известно дифференциальное уравнение, описывающее поведение биологического объекта.

Например, если объект описывается системой уравнений вида (2.11), то для определения параметров {ai, bi} выбирается класс возмущающих стимулов {xicm}, подаваемых на вход объекта.

65

	dyi		(2.11)
	dt + ai yi = bi f (x)

Наблюдаемая в эксперименте реакция объекта {yip }сравни-

вается с реакцией модели {yi } и, с помощью критерия согласия определяются параметры уравнения модели {ai , bi }.

Применение метода оценивания параметров дифференциального уравнения можно рассмотреть на примере идентификации биологического звена биотехнической системы инфузионного введения лекарственных препаратов в организм человека. Система предназначена для длительного непрерывного дозированного введения лекарственных препаратов в кровяное русло, что позволяет в ряде случаев повысить эффективность лечения и сократить суммарную дозу препарата.

Рисунок 2.3 – БТС инфузионного введения лекарственного препарата в кровяное русло

Техническое звено системы содержит шприц с лекарственным препаратом, соединенный с пациентом с помощью венозного катетера. Поршень шприца перемещается с помощью электрического привода, со скоростью задаваемой программой заложенной в контроллере.

Целевая функция системы – получение требуемого терапевтического эффекта, за счет достижения заданной концентрации препарата в тканях-адресатах. Одна из областей использования по-

66

добных систем – управляемая внутривенная анестезия при проведении длительных хирургических операций. Здесь ставится задача поддержания необходимой концентрации препарата – анестетика, обеспечивающей требуемую глубину наркоза при минимизации расхода препарата.

В соответствии с целевой функцией модель системы будем искать в виде:

C = f {U, t}

(2.12)

где: C – концентрация препарата; U – скорость введения препарата, задаваемая программой контроллера.

Проведем анализ биологического звена БТС. Под действием возвратно-поступательного электромеханического привода, воздействующего на поршень шприца, лекарственный препарат через венозный катетер поступает в кровеносный сосуд и, далее, с током крови разносится по организму. Изменение концентрации препарата в тканях-адресатах определяется протеканием следующих процессов:

-скоростью введения и переноса лекарственного вещества с током крови;

-накоплением препарата в тканях;

-диффузией вещества в тканях из области высокой концентрации в область низкой концентрации;

-элиминацией вещества (удаление из крови почками, разрушение в печени).

Для первого приближения моделирования биологического звена системы, можно ограничиться учетом двух факторов: поступлением вещества в ткани и его элиминацией.

В соответствии с законами фармакокинетики темпы изменения компонент системы связаны с их уровнями:

	dy	n	l
		= ∑xk − ∑xm		(2.13)
	dt
		1	1

где: y – уровень (объем) вещества; xk – темпы поступления вещества; xm – темпы элиминации вещества.

67

Для рассматриваемой системы, уравнение (2.13) принимает

вид:

	dC	=	U	− KэC	(2.14)
	dt		V

где: V – объем циркулирующей крови; Kэ – коэффициент элими-

нации.

Для идентификации биологического звена системы необходимо определить Kэ .

Решение уравнения в операторном виде имеет вид:

pC( p) =		1		U( p) − KэC( p)			(2.15)
	V
C( p) =	1		U ( p)		1		(2.16)
	V				p + Kэ

Для идентификации системы можно воспользоваться ступенчатым тестовым воздействием, которое реализуется путем включения привода инфузионного дозатора в режиме постоянной скорости подачи препарата. Моделью такого воздействия является единичная функция:

U(t) = 1(t) U0

Для решения операторного уравнения (2.16) подставим в качестве входного воздействия:

U ( p) = 1p U0

Тогда решение уравнения модели (2.16) примет вид:

	C( p) =	U		1
		V		p( p + Kэ )

C(t) = L−1{C( p)}

C(t) = Cуст[1− exp(−tKэ )]

где: Cуст =U0 KэV

(2.17)

(2.18)

(2.19)

При включении инфузии постоянная времени достижения установившегося уровня концентрации определяется величиной

68

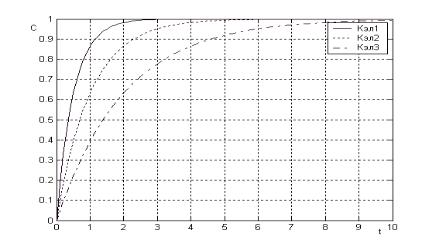
коэффициента элиминации Kэ , зависящего от свойств лекарственного вещества.

Рисунок 2.4 – Изменение концентрации препарата во времени при включении инфузии с постоянной скоростью для различных коэффициентов элиминации (Кэл1> Кэл2> Кэл3)

Для идентификации модели инфузионной системы необходимо определить значение коэффициента элиминации. Экспериментальную зависимость изменения концентрации препарата во времени в области расположения ткани-адресата в ответ на тестовое воздействие можно зарегистрировать, например, с помощью метода радиоактивной метки. Затем путем обработки данных по методу наименьших квадратов можно определить параметры модели.

На практике, в системах инфузионной анестезии для определения коэффициента элиминации Kэ , используют фиксацию мо-

мента времени «засыпания» пациента на операционном столе, определяемого по моменту закрывания глаз под действием анестетика. Считается, что величина промежутка времени от включения инфузии до момента закрывания глаз связана с постоянной времени процесса установления концентрации препарата. Эта величина вводится в контроллер устройства для использования в уравнении

69