1. Множества натуральных, целых, рациональных чисел.
1. Натуральные числа − числа, используемые при счете (перечислении) предметов: N = {1, 2, 3, ...}
1,2. Натуральные числа с включенным нулем − числа, используемые для обозначения количества предметов: N0 = {0, 1, 2, 3, ...}
2. Целые числа − включают в себя натуральные числа, числа противоположные натуральным(т.е. с отрицательным знаком) и ноль. Целые положительные числа: Z + = N = {1, 2, 3, ...} Целые отрицательные числа: Z − = {..., −3, −2, −1} Z = Z − ∪ {0} ∪ Z + = {..., −3, −2, −1, 0, 1, 2, 3, ...}
3. Рациональные числа − числа, представляемые в виде обыкновенной дроби a/b, где a и b − целые числа и b ≠ 0. Q = {x | x = a/b, a ∈ Z, b ∈ Z, b ≠ 0} При переводе в десятичную дробь рациональное число представляется конечной или бесконечной периодической дробью.
Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b,c, ...}, где в фигурных скобках указаны элементы множества A.
Будем пользоваться обозначениями:
N - множество всех натуральных чисел; Z - множество всех целых чисел; Q - множество всех рациональных чисел; R - множество всех действительных чисел; C - множество всех комплексных чисел; Z0 - множество всех неотрицательных целых чисел.
Запись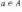 
(или 
)
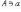означает, что элемент a принадлежит
множеству A.
Запись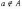 
(или 
)
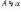означает, что элемент a не
принадлежит множеству A.
2. Множество действительных чисел.
Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел.
Действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль.
Действительные числа разделяются на рациональные и иррациональные.
Вещественные (действительные) числа - это своего рода математическая абстракция, служащая для представления физических величин. Такие числа могут быть интуитивно представлены как отношение двух величин одной размерности, или описывающие положение точек на прямой. Множество вещественных чисел обозначается и часто называется вещественной или числовой прямой. Формально вещественные числа состоят из более простых объектов таких, как целые и рациональные числа. Множество действительных чисел обозначается - R
3. Последовательность. Понятие последовательности
Если функция определена на множестве натуральных чисел N, то такая функция называется бесконечной числовой последовательностью. Обычно числовые последовательность обозначают как(Xn), где n принадлежит множеству натуральных чисел N.
Числовая последовательность может быть задана формулой. Например, Xn=1/(2*n). Таким образом мы ставим в соответствие каждому натуральному числу n некоторый определенный элемент последовательности (Xn).
Если теперь последовательно брать n равными 1,2,3, …., мы получим последовательность (Xn): ½, ¼, 1/6, …, 1/(2*n), …
Виды последовательности:
Последовательность может быть ограниченной или неограниченной, возрастающей или убывающей.
Последовательность (Xn) называет ограниченной, если существуют два числа m и M такие, что для любого n принадлежащего множеству натуральных чисел, будет выполняться равенство m<=Xn
Последовательность (Xn), не являющаяся ограниченной, называется неограниченной последовательностью.
Последовательность (Xn) называется возрастающей, если для всех натуральных n выполняется следующее равенство X(n+1) > Xn. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена.
Последовательность (Xn) называется убывающей, если для всех натуральных n выполняется следующее равенство X(n+1) < Xn. Иначе говоря, каждый член последовательности, начиная со второго, должен быть меньше предыдущего члена.
Пример последовательности
Проверим, являются ли последовательности 1/n и (n-1)/n убывающими.
Если последовательность убывающая, то X(n+1) < Xn. Следовательно X(n+1) – Xn < 0.
1/n:
X(n+1) – Xn = 1/(n+1) – 1/n = -1/(n*(n+1)) < 0. Значит последовательность 1/n убывающая.
(n-1)/n:
X(n+1) – Xn =n/(n+1) - (n-1)/n = 1/(n*(n+1)) > 0. Значит последовательность (n-1)/n возрастающая.