4. Предел последовательности.

Число A называется пределом числовой последовательности {an}, если для любого, даже сколь угодно малого положительного числа ε > 0, найдется такое число N, зависящее от ε, что для всех членов последовательности с номерами n > N верно неравенство:

Общепринятое обозначение предела последовательности:

Это неравенство можно интерпретировать следующим образом: все

члены последовательности, начиная с некоторого попадают в ε-окрестность

точки A. Поскольку число ε может быть сколь угодно малым, это

гарантирует сходимость последовательности к пределу A.

5. Предел функции. Предел функции при

Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :

(1)

сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность

(2)

и можно ставить вопрос о существовании её предела.

Определение 1. 

Число A называется пределом функции f(x) в точке (или при ), если для любой сходящейся к последовательности (1) значений аргумента x, отличных от , соответствующая последовательность (2) сходится к числу A.

Символически это записывается так: 

Предел функции при , при и при

Кроме рассмотренного понятия предела функции при 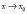существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение 2. Число A называется пределом функции f(x) при , если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: .

Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: ().

6. Свойства пределов функции

1.   Предел суммы/разности двух функций равен сумме/разности их пределов:

2.   Предел произведения двух функций равен произведению их пределов:

3.   Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

4.   Константу можно выносить за знак предела:

5.   Предел степени с натуральным показателем равен степени предела:

7. Первый замечательный предел

Первый замечательный предел:

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Следствия из первого замечательного предела

1.   

2.   

3.   

4.   

8. Второй замечательный предел

Второй замечательный предел:

здесь е - число Эйлера.

Следствия из второго замечательного предела:

1.   

2.   

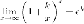
3.   

4.   

5.   

6.   

9. Определение производной

Производной от функции в точке 

 называется предел отношения приращения функции к приращению

аргумента  :  при , если он существует, то есть:

Или

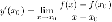
10. Производная суммы, разности, произведения и частного функций.

Производная суммы равна сумме производных:

Производная разности равна разности производных:

Производная произведения равна производная первой функции на вторую плюс первая функция, умноженная на производную второй:

Производная частного равна производная числителя, умноженная на знаменатель, минус производная знаменателя, умноженная на числитель, и разность делится на знаменатель в квадрате:

11. Производная сложной функции.

12. Производные основных элементарных функций.

13. Производные высших порядков.

Если функция имеет производную в каждой точке своей области определения, то ее производная есть функция от . Функция , в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом .

Таким образом

14. Правило Лопиталя.

Пусть функции и удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки  ;

2) и в этой окрестности;

3)  ;

4) существует конечный или бесконечный.

Тогда существует и  , причем  

Правило Лопиталя распространяется на случай неопределенности

типа  при.

15. Исследование функции на монотонность и экстремумы с помощью производной.

Функция  строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.

Если производная функции 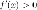 на некотором промежутке 

то функция  возрастает на этом промежутке; если же 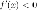  на промежутке , то функция   убывает на этом промежутке.

Экстремум - максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Простой алгоритм нахождения экстремумов. - Находим производную функции - Приравниваем эту производную к нулю - Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль) - Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум - Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную. Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом. Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.