
- •Формула Бейеса (Байеса)
- •Свойства дисперсии
- •Формула Бернулли
- •Пример 1
- •Формула Пуассона
- •Пример 2
- •15.) Числовые характеристики непрерывной случайной величины
- •Критерии, основанные на нормальном распределении Сравнение выборочного среднего арифметического со средним значением генеральной совокупности
- •16.) Доверительный интервал и доверительная вероятность
- •ОпределениеПравить
- •17.) Генеральная и выборочная совокупности
16.) Доверительный интервал и доверительная вероятность
Стандартный интервал а</=х</=b
Вероятность попадания в него случайной величины
b
Р(а</=х</=b)=
а р
(плотность) (Х)dx
р
(плотность) (Х)dx
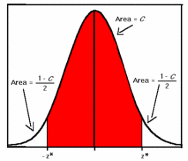
Доверительная вероятность α – некоторая заданная вероятность, с которой случ.величина попадает в определённый интервал.
Такой интервал – доверительный. Стандартные интервалы
(вместо < должно быть </=)
М- σ <х< М+ σ (α = 68%)
М- 2σ <х< М+ 2σ (α = 95%)
М- 3σ <х< М+ 3σ (α = 99,7%)
Доверительный интервал в математической статистике - это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой что он содержит этот параметр с заданной вероятностью.
ОпределениеПравить
Пусть  есть
выборка из распределения
есть
выборка из распределения  ,
где
,
где 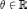 -
неизвестный параметр. Пусть также
задана
-
неизвестный параметр. Пусть также
задана  .
Тогда случайный интервал
.
Тогда случайный интервал  ,
где
,
где

есть некоторые статистики имеющейся выборки, такой что
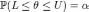 ,
,
называется  -доверительным
интервалом для параметра
-доверительным
интервалом для параметра  .
.
 (доверительный
интервал для нормального распределение)
(доверительный
интервал для нормального распределение)
17.) Генеральная и выборочная совокупности
 Генеральной
совокупностью называют
совокупность всех мысленно возможных
объектов данного вида, над которыми
проводятся наблюдения с целью получения
конкретных значений случайной величины,
или совокупность результатов всех мыслимых
наблюдений, проводимых
в неизменных условиях над одной из
случайных величин, связанных с данным
видом объектов.
Генеральной
совокупностью называют
совокупность всех мысленно возможных
объектов данного вида, над которыми
проводятся наблюдения с целью получения
конкретных значений случайной величины,
или совокупность результатов всех мыслимых
наблюдений, проводимых
в неизменных условиях над одной из
случайных величин, связанных с данным
видом объектов.
Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки.
 Выборочной
совокупностью называют часть отобранных
объектов из генеральной совокупности.
Выборочной
совокупностью называют часть отобранных
объектов из генеральной совокупности.
(
Генеральная
средняя.
Пусть изучается генеральная совокупность
относительно количественного признака
Х. Генеральной средней называют среднее
арифметическое значений признака
генеральной совокупности. Если все
значения признака различны, то
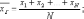 Если
значения признака имеют частоты N1, N2,
…, Nk, где N1 +N2+…+Nk= N, то
Если
значения признака имеют частоты N1, N2,
…, Nk, где N1 +N2+…+Nk= N, то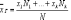
.Выборочная
средняя.
Пусть для изучения генеральной
совокупности относительно количественного
признака Х извлечена выборка объема n.
Выборочной средней называют среднее
арифметическое значение признака
выборочной совокупности. Если все
значения признака выборки различны, то
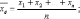 если же все значения имеют частоты n1,
n2,…,nk, то
если же все значения имеют частоты n1,
n2,…,nk, то
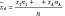 Выборочная
средняя является несмещенной и
состоятельной оценкой генеральной
средней. )
Выборочная
средняя является несмещенной и
состоятельной оценкой генеральной
средней. )
Число наблюдений, образующих выборку, называется объемом выборки.
Репрезентативности выборки - полнота и адекватность свойств генеральной совокупности, по отношению к которой эту выборку можно считать представительной.
Точечная и интервальная оценка параметра генеральной совокупности. Предположим, что по выборке нужно найти не интервал, в котором находится параметр, а одно число которое ближе всего к параметру. Под оценкой понимается любое число, рассчитанное по выборке и характеризующее параметр.Свойства точечной оценки: Несмещенность – среднее выборочного распределения оценки равно величине параметра. Состоятельность – при увеличении объема выборки оценка приближается к значения измеряемого параметра. Эффективность – чем ниже дисперсия, т.е. чем меньше отличаются оценки, полученные в разных выборках, тем выше эффективность.
Средняя арифметическая - такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий фонд заработной платы — это сумма заработных плат всех работников.
Средняя арифметическая может быть вычислена по формуле:
где n — численность совокупности.
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
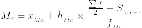
XMe -нижняя граница медианного интервала
hMe -величина медианного интервала;
SMe-1-сумма накопленных частот интервала, предшествующего медианному интервалу;
fMe -локальная частота медианного интервала.
Мода (Mo) − величина, наиболее часто встречающаяся в данной совокупности. В вариационном ряду это − варианта, имеющая наибольшую частоту. Медианой (Me) называют варианту, которая является серединой упорядоченного (ранжированного) вариационного ряда, т. е. делит его на две равные части: одна часть имеет значения вариационного признака, меньшие средней, другая − бóльшие. Медиана указывает на значение вариационного признака, которого достигла половина единиц совокупности.
Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.

ХМ0 — нижняя граница модального интервала;
hMo - величина (шаг, ширина) модального интервала;
f1 - локальная частота интервала, предшествующего модальному;
f2 - локальная частота модального интервала;
f3 - локальная частота интервала, следующего за модальным.
Модальный интервал определяется по наибольшей частоте.
18.) характеристики рассеяния Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Среднее абсолютное отклонение (mean absolute deviation) =арифметическое среднее отклонений всех значений от среднего. Абсолютным оно является потому, что суммируются отклонения по модулю, так как в противном случае сумма всех разбросов была бы равна нулю. Формула среднего абсолютного отклонения: Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии. ,
где символ обозначает выборочное среднее.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
Для
исправления выборочной дисперсии
достаточно умножить ее на дробь
получим исправленную дисперсию S2. Исправленная дисперсия является несмещенной оценкой.
В качестве оценки генеральной дисперсии принимают исправленную дисперсию.
Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение
19.) абсолютная и относительная погрешности любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение:
Апр- DА < Аист < Апр+ DА
Величина DА называется абсолютной погрешностью измерения величины А. Абсолютная погрешность выражается в единицах измеряемой величины. Абсолютная погрешность равна модулю максимально возможного отклонения значения физической величины от измеренного значения. Апр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений.
Но для оценки качества измерения необходимо определить относительную погрешность e. e= DА/Апр или e= (DА/Апр)*100%.
Если при измерении получена относительная погрешность более 10%, то говорят, что произведена лишь оценка измеряемой величины. В лабораториях физического практикума рекомендуется проводить измерения с относительной погрешностью до 10%. В научных лабораториях некоторые точные измерения (например определение длины световой волны), выполняются с точностью миллионных долей процента.
Окончательный результат измерения физической величины А следует записывать в такой форме;
А=Апр+ D А, e= (DА/Апр)*100%.
Апр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений. D А- полная абсолютная погрешность прямого измерения.
При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Хпр, пользуясь формулами, приведенными в таблице (без доказательств).
Абсолютную погрешность определяется по формуле DХ=Хпр *e,
где e выражается десятичной дробью, а не в процентах.
Окончательный результат записывается так же, как и в случае прямы
20.) Факторная и остаточная дисперсия
21.) дискретные и непрерывные временные ряды,их характеристики.Уравнение тренда.Сглаживание временных рядов:метод скользящего среднего.
Последовательность результатов наблюдений над некоторой величиной полученных последовательно во времени,наз.- временным рядом.Например:последовательность значений температуры тела больного в течение суток если ее регистрацию проводили каждый час.
Величина случайного временного ряда в произвольный момент времени,может быть описана соответствующей функцией распределения и для такого ряда могут быть определеныосновные числовые характеристики,т.е. математическое ожидание,дисперсия и среднее квадратичное отклонение.В общем случае произвольного ряда эта функция распределения явл.функцией времени и такое ряд называют нестационарным.В то же время ряды,функция распределения значений которых не зависит от времени наз.- стационарным.Стационарные:их числовые характеристики не зависят от времени.
х1,х2….значение
этого ряда полученных последовательно
в течение некоторого периода наблюдения.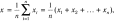
n-кол-во экспериментальных значений.
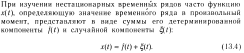 На
практике часто возникает необходимость
выявления основной тенденции изменения
временного ряда(наз.- трендом)т.е.
нахождения функции f(t)=at+b,где
а,b
коэффициенты.которые можно определить
используя метод наименьших квадратов.
На
практике часто возникает необходимость
выявления основной тенденции изменения
временного ряда(наз.- трендом)т.е.
нахождения функции f(t)=at+b,где
а,b
коэффициенты.которые можно определить
используя метод наименьших квадратов.
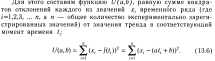
Сглаживание- дисперсия ряда уменьшается и он становится более плавным.Выбирают некоторый временной нтервал усреднения который как правило значительно меньше всего времени наблюдения за значениями врем. ряда,и с помощью этого интервала скользят вдоль ряда производя усреднение значений ряда,попадающих в этот скользящий
интервал.
22.)
статистические гипотезы.Нулевая и
конкурирующая гипотезы.Параметрический
критерий Стьюденса.
Пусть в (статистическом) эксперименте
доступна наблюдению случайная
величина  , распределение которой
, распределение которой  известно
полностью или частично. Тогда любое
утверждение,
известно
полностью или частично. Тогда любое
утверждение,
касающееся  называется статистической
гипотезой.
называется статистической
гипотезой.

Если вид распределения или функция распределения выборки нам заданы, то в этом случае задача оценки различий двух групп независимых наблюдений может решаться с использованием параметрических критериев статистики: либо критерия Стьюдента (t), если сравнение выборок ведется по средним значениям (X и У). В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения t осуществляется по формуле:
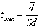 (5)
(5)
где 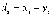 —
разности между соответствующими
значениями переменной X и переменной
У, а d -
среднее этих разностей;Sd вычисляется
по следующей формуле:
—
разности между соответствующими
значениями переменной X и переменной
У, а d -
среднее этих разностей;Sd вычисляется
по следующей формуле:
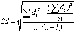 (6)
(6)
Число степеней свободы k определяется по формуле k=n-1.
23.)
статистические гипотезы.
Пусть в (статистическом) эксперименте
доступна наблюдению случайная
величина  , распределение которой
, распределение которой  известно
полностью или частично. Тогда любое
утверждение, касающееся
известно
полностью или частично. Тогда любое
утверждение, касающееся 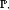 называется статистической
гипотезой.
Статистическая гипотеза, однозначно
определяющая распределение
называется статистической
гипотезой.
Статистическая гипотеза, однозначно
определяющая распределение  ,
то есть
,
то есть 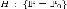 ,
где
,
где  какой-то
конкретный закон, называется простой.Статистическая
гипотеза, утверждающая принадлежность
распределения
какой-то
конкретный закон, называется простой.Статистическая
гипотеза, утверждающая принадлежность
распределения  к
некоторому семейству распределений,
то есть вида
к
некоторому семейству распределений,
то есть вида 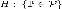 ,
где
,
где  —
семейство распределений, называется сложной.
—
семейство распределений, называется сложной.
На
практике обычно требуется проверить
какую-то конкретную и как правило простую
гипотезу  .
Такую гипотезу принято называть нулевой.
При этом параллельно рассматривается
противоречащая ей гипотеза
.
Такую гипотезу принято называть нулевой.
При этом параллельно рассматривается
противоречащая ей гипотеза 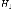 ,
называемая конкурирующей.
Для преодоления указанных трудностей
в практике педагогических исследований
следует использовать непараметрические критерии статистики,
такие, как критерий знаков, двухвыборочный
критерий Вилкоксона, критерий Ван дер
Вардена, критерий Спирмена, выбор
которых, хотя и не требует большого
числа членов выборки и знаний, вида
распределения, но все же зависит от
целого ряда условий.
,
называемая конкурирующей.
Для преодоления указанных трудностей
в практике педагогических исследований
следует использовать непараметрические критерии статистики,
такие, как критерий знаков, двухвыборочный
критерий Вилкоксона, критерий Ван дер
Вардена, критерий Спирмена, выбор
которых, хотя и не требует большого
числа членов выборки и знаний, вида
распределения, но все же зависит от
целого ряда условий.
24.)
коэффициент корреляции
и коэффициент
частной корреляции — статистическая взаимосвязь
двух или нескольких случайных
величин (либо
величин, которые можно с некоторой
допустимой степенью точности считать
таковыми). При этом изменения значений
одной или нескольких из этих величин
сопутствуют систематическому изменению
значений другой или других
величин.[1] Математической
мерой корреляции двух случайных величин
служит корреляционное
отношение  [2],
либо коэффициент
корреляции
[2],
либо коэффициент
корреляции  (или
(или  )[1].
В случае, если изменение одной случайной
величины не ведёт к закономерному
изменению другой случайной величины,
но приводит к изменению другой
статистической характеристики данной
случайной величины, то подобная связь
не считается корреляционной, хотя и
является статистической.
)[1].
В случае, если изменение одной случайной
величины не ведёт к закономерному
изменению другой случайной величины,
но приводит к изменению другой
статистической характеристики данной
случайной величины, то подобная связь
не считается корреляционной, хотя и
является статистической.


25.)
линии регрессии.
Пусть  и
и  -
две случайные непрерывные величины,
находящиеся в корреляционной зависимости.
Это значит, что каждому значению x случайной
величины
-
две случайные непрерывные величины,
находящиеся в корреляционной зависимости.
Это значит, что каждому значению x случайной
величины 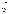 соответствует
вполне определенное распределение
вероятностей величины
соответствует
вполне определенное распределение
вероятностей величины 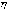 .
Плотность
.
Плотность  распределения
величины
распределения
величины  при
условии, что
при
условии, что 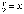 ,
называется условной
плотностью распределенияслучайной
величины
,
называется условной
плотностью распределенияслучайной
величины 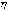 .
Вычислим
для данного случая так называемое условное
математическое ожидание
.
Вычислим
для данного случая так называемое условное
математическое ожидание 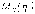 величины
величины 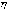 при
условии, что
при
условии, что 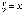 . Согласно
определению математического ожидания
непрерывной случайной величины, имеем
. Согласно
определению математического ожидания
непрерывной случайной величины, имеем
 Каждому
возможному значению x случайной
величины
Каждому
возможному значению x случайной
величины 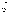 соответствует
определенное значение условного
математического ожидания
соответствует
определенное значение условного
математического ожидания 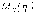 .
Таким образом, мы получаем
функцию
.
Таким образом, мы получаем
функцию  переменной x.
Эта функция y=f(x) называется функцией
регрессии величины
переменной x.
Эта функция y=f(x) называется функцией
регрессии величины 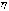 на
на 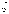 ,
а ее график - линией
регрессии
,
а ее график - линией
регрессии  на
на 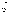 . Аналогично
определяется условное
математическое ожидание величины
. Аналогично
определяется условное
математическое ожидание величины 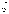 при
условии, что
при
условии, что 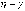 :
:
 где
где 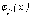 -
условная плотность вероятности случайной
величины
-
условная плотность вероятности случайной
величины 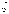 при
условии, что
при
условии, что 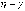 .
Функция x=g(y) называется функцией
регрессии величины
.
Функция x=g(y) называется функцией
регрессии величины 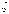 на
на 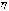 ,
а ее график - линией
регрессии
,
а ее график - линией
регрессии  на
на 
Метод
наименьших квадратов
заключается в нахождении коэффициентов
линейной зависимости, при которых
функция двух переменных а и b 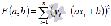 принимает
наименьшее значение. То есть, при
данных а и b сумма
квадратов отклонений экспериментальных
данных от найденной прямой будет
наименьшей. В этом вся суть метода
наименьших квадратов.
принимает
наименьшее значение. То есть, при
данных а и b сумма
квадратов отклонений экспериментальных
данных от найденной прямой будет
наименьшей. В этом вся суть метода
наименьших квадратов.
Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
