Лекции по Матанализу ч

A 1;

B 2;

C 3/ 2;

D 6;

9 / 2;

(4x

3

9

2

2

3

2

2

2

6x) x

3dx

x

2x

x 6

x

3

ln

x

x

3

C.

Пример.

2

2

1

dx

x

;

v3 dv

v2 dv

v

( Av B) 1 v 2

x3

dv

v2

x2 1

1

1 v2

dx

1

2

2

v

v

v2

( Av B)v

A

1 v2

1 v2

1 v2

1 v2

v2 A Av 2 Av 2 Bv

v2 2Av 2 Bv A

A 1/ 2;

B 0;

1/ 2;

v2 dv

v 1 v

2

1

1

x2

1

1

arcsin v

arcsin

C

1 v

2

2

2

2

x

2

x

Второй способ решения того же самого примера.

dv

1 v2

1

tgt

dx

x

; dx

dt;

cos t

cos t

x3

x 2 1

x

2

1 tgt;

1

1

1

1 cos 2t dt

t

sin 2t

sin

2

2

4

1

1

x 2 1

arccos

C.

2

x

x

2

sin t

cos

2

t

dt

sin t cos

4

t

dt cos 2 tdt

1

cos

2

t sin t

tgt

cos3 t

1

x

2

1

2t 2 sin t cos t 2

x

x

		С		учетом		того,		что функции arcsin и arccos связаны	соотношением
	arcsin	1			arccos	1	, а	постоянная интегрирования С – произвольное	число, ответы,
		x		2		x

полученные различными методами, совпадают.

Как видно, при интегрировании иррациональных функций возможно применять различные рассмотренные выше приемы. Выбор метода интегрирования обуславливается в основном наибольшим удобством, очевидностью применения того или иного метода, а также сложностью вычислений и преобразований.

Пример.

x sin t;

dx

cos tdt

dt

x

dx cos tdt;

tgt C

C.

(1

x

2

)

3 / 2

cos

3

t

cos

2

cos t

t

1 x

2

1 x 2

Несколько примеров интегралов, не выражающихся через элементарные функции.

К таким интегралам относится интеграл вида R(x,			)dx , где	P x -
		P(x)			многочлен
степени выше второй. Эти интегралы называются эллиптическими.
Если степень многочлена P x	выше четвертой, то интеграл				называется

ультраэллиптическим.

21

Если все – таки интеграл такого вида выражается через элементарные функции, то он называется псевдоэллиптическим.

	Не могут быть выражены через элементарные функции следующие интегралы:
1)	e x2 dx - интеграл Пуассона ( Симеон Дени Пуассон – французский математик (1781-
	1840))
2)	sin x2 dx;	cos x2 dx - интегралы Френеля (Жан Огюстен Френель – французский

ученый (1788-1827) - теория волновой оптики и др.)

3)lndxx - интегральный логарифм

4)exx dx - приводится к интегральному логарифму

5)sinx x dx - интегральный синус

6)cosx xdx - интегральный косинус

22

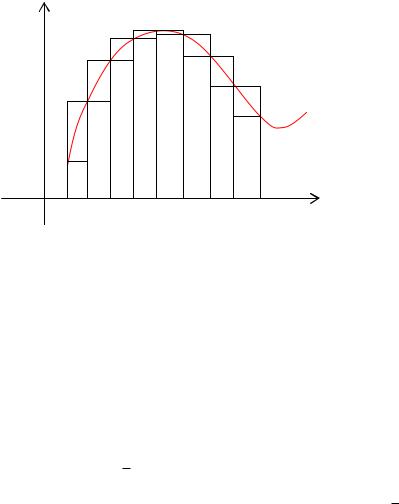
Определенный интеграл.

Определение определённого интеграла.

Пусть на отрезке a,b задана непрерывная функция f x .

y M

m
0	a	xi	b	x

Обозначим m и M наименьшее и наибольшее значение функции на отрезке a,b Разобьем отрезок a,b на части (не обязательно одинаковые) n точками.

x0 x1 xn

Тогда xi xi 1 xi , i 1, , n ;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

xi 1, xi mi , Mi

Составим суммы:

n

S n mi xi i 1

n

Sn Mi xi

i 1

Сумма S n называется нижней интегральной суммой Дарбу, а сумма S n – верхней

					Mi , то S n				n , и следовательно
интегральной суммой Дарбу, причём, т.к. mi								S
	m b a S n						n M b a
						S
Внутри каждого отрезка xi 1, xi выберем некоторую точку i .
			xi 1 i xi
Найдем значения функции в этих точках и составим выражение, которое называется
интегральной суммой для функции f x на отрезке a,b .
			n
			n f ( i ) xi
			i 1
Тогда можно записать: mi xi f i xi					Mi xi
n	n				n
Следовательно, mi xi f ( i ) xi					Mi xi
i 1	i 1				i 1
		Sn n Sn			(1)

Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.

23

Наибольший

отрезок

разбиения

max xi

называется

шагом

разбиения.

Если

max xi 0 , то число отрезков разбиения отрезка

a,b стремится к бесконечности.

Определение определённого интеграла: Если при любых разбиениях отрезка a,b

таких, что

max xi 0

и

произвольном

выборе

точек

i

интегральная

сумма

n

n f ( i ) xi

стремится

к

пределу

S ,

то

этот

предел

называется

определенным

i 1

x

отрезке a,b .

интегралом от

функции

f

на

В

этом

случае

функция называется

интегрируемой по Риману на отрезке a,b .

b

n

Обозначение: f (x)dx

lim

n

lim

f ( i ) xi

a

max xi 0

max xi 0

i 1

a,b – отрезок

a – нижний предел, b

– верхний предел,

x – переменная интегрирования,

интегрирования.

f x

Эквивалентное определение. Функция

является интегрируемой по Риману на

отрезке a,b если верхняя и нижняя суммы Дарбу имеют общий предел, т.е.

n

n

b

lim

S

lim

S

lim

m x

lim

M

x

f (x)dx

max xi

0

n

max xi

0

n

max xi

0 i 1

i

i max xi 0 i 1

i

i

a

Это следует из того, что если

S n то в силу неравенства (1)

lim

Sn

lim

max xi

0

max

xi 0

оба эти предела равны S . С другой стороны если эти пределы неравны, то предел n

будет

зависеть от способа разбиения. Следовательно, функция

f x

не будет интегрируемой.

Теорема (необходимое и достаточное условие интегрируемости).

Для того, чтобы ограниченная на отрезке

a,b

функция

f x

была интегрируемой

n S n

необходимо и достаточно, чтобы разность

S

стремилась к нулю при любом способе

разбиения отрезка

a,b и при стремлении

шага разбиения к нулю.

Доказательство. Необходимость следует из того, что если

Sn

и

S n

имеют общий

предел, то

S

n S n

0

при n и max xi 0 .

0 имеем

Достаточность. Из неравенства Sn n

Sn

следует, что при

S

n S n

b

n S f (x)dx

lim

Sn

lim

S n

lim

max

xi 0

max xi 0

max xi 0

a

Теорема: Если функция

f x

непрерывна на отрезке a,b ,

то она интегрируема на

этом отрезке.

Доказательство.

В самом деле, для непрерывной функции для любого найдётся

число , что неравенство

справедливо если

x1 x2

.

f x1 f x2

b a

Пусть все отрезки разбиения меньше , т.е.

xi 1 xi

. Тогда верхняя и нижняя

грани функции

f x удовлетворяют неравенству

M i mi

b a

Следовательно, верхняя и нижняя суммы Дарбу удовлетворяют условию

n

n

Sn S n

M i mi

xi

xi

i 1

24

b a i 1

Т.е. Sn S n 0 при n и 0 , что даёт условие интегрируемости.

Теорема. Если функция f x ограничена на отрезке a,b и имеет не более конечного

числа точек разрыва, то она интегрируема на этом отрезке.

Замечание. То, что функция имеет конечное число точек разрыва существенно. Здесь в качестве примера можно рассмотреть функцию Дирихле

1,

x рациональное число

x 0,1

f x

x иррациональное число

,

0,

Так как любой промежуток разбиения сожержит как рациональные точки, так и

иррациональные, то Sn 0, Sn 1. Следовательно, эта функция не интегрируема.

Теорема. Монотонная огараниченная на a,b функция всегда интегрируема.

Доказательство. Пусть f x

- монотонно возрастающая на a,b функция. Тогда её

колебания в промежутке xi , xi 1 будут

i f xi 1 f xi

Зададимся любым 0 и положим

f b f a

Если xi будем иметь

n

n

f xi f b f a

i xi

f xi 1

i 1

i 1

Свойства определенного интеграла.

b

b

1) Af (x)dx A f (x)dx;

a

a

b

b

b

2) ( f1 (x) f2 (x))dx f1 (x)dx f 2 (x)dx

a

a

a

a

3)

f (x)dx 0

a

b

b

4)

Если f x x на отрезке a,b , a b , то

f (x)dx (x)dx

a

a

Для доказательства необходимо составить интегральные суммы для f x и x и

перейти к пределу.

f x

5)

Если m и M – соответственно наименьшее и наибольшее значения функции

на отрезке a,b , то:

b

m(b a) f (x)dx M (b a)

a

m b a Sn n

M b a .

Доказательство

следует

из

неравенства

Sn

Далее

необходимо перейти к пределу.

f x непрерывна на отрезке a,b ,

6) Первая теорема о среднем. Если функция

то на

этом отрезке существует точка такая, что

b

f (x)dx (b a) f ( )

a

Доказательство:

В соответствии со свойством 5:

25

					1	b
				m		f (x)dx M
					b a
						a
				f x непрерывна на отрезке			a,b , то она принимает на этом отрезке все
	т.к. функция
	значения от m до М. Другими словами, существует такое число a,b , что если
	1		b				b
			f (x)dx и f , а		a b , тогда f (x)dx (b a) f ( ) .
		b a
			a				a
	Теорема доказана.
		b		a
	7) f (x)dx f (x)dx
		a		b
	8) Для произвольных чисел a, b, c справедливо равенство:
				b	c		b
				f (x)dx		f (x)dx f (x)dx
				a	a		c

Разумеется, это равенство выполняется, если существует каждый из входящих в него

интегралов. Для доказательства необходимо составить интегральные суммы для каждого из промежутков и перейти к пределу.

Обобщенная теорема о среднем. Если функции f x и x непрерывны на отрезкеa,b , и функция x знакопостоянна на нем, то на этом отрезке существует точка , такая, что

b			b
f (x) (x)dx f ( ) (x)dx
a			a
Вторая теорема о среднем.		Если в промежутке a,b			функция f x	монотонно
убывает, а x - интегрируема, то
b			b
f (x) (x)dx	f (a) (x)dx f (b)			(x)dx,	a b
a		a
Формула Ньютона-Лейбница
b
Пусть в интеграле f (x)dx		нижний	предел	a const , а верхний		предел b

a

изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.

			x		Найдем производную функции x по переменному
		Обозначим f (t)dt x .
			a
верхнему пределу x (Применяется теорема о среднем).
						x x
	d	x		x x x		f (t)dt		f x	x, x x f (x)
		f (t)dt lim			lim	x	lim
	dx			x		x		x
		a	x 0		x 0		x 0
		Следовательно, x является первообразной для f x

Упражнение. Доказать, что

d b f (t)dt f (x) dx x

Таким образом, доказана следующая теорема.

26

Теорема: Для всякой функции f x , непрерывной на отрезке a,b , существует на

этом отрезке первообразная, а значит, существует неопределенный интеграл. Теорема: (Теорема Ньютона – Лейбница)

Если функция F x – какаялибо первообразная от непрерывной функции f x , то

b

f (x)dx F (b) F (a)

a

это выражение известно под названием формулы Ньютона – Лейбница.

Доказательство: Пусть F x – первообразная функции f x . Тогда в соответствии с

x	f x . Но т.к.
приведенной выше теоремой, функция f (t)dt - первообразная функция от
a

функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

x

f (t)dt F (x) C

a

при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

a
f (t)dt F (a) C		0 F(a) C	C F(a)
a
x
Тогда f (t)dt F (x) F (a) .
a

b

А при х = b: f (t)dt F (b) F (a)

a

Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

b

f (x)dx F (b) F (a)

a

Теорема доказана.

Иногда применяют обозначение F b F a F x ba .

Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.

Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.

Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.

Методы вычисления определенного интеграла.

Замена переменных.

b

Пусть задан интеграл f (x)dx , где f x – непрерывная функция на отрезке a,b .

a

Введем новую переменную в соответствии с формулой x t . Тогда если

1) a, b

27

2)t и t непрерывны на отрезке ,

3)f t определена на отрезке , ,

	b
	Тогда	f (x)dx		F[ ( )] F[ ( )] F (b) F (a)
			f [ (t)] (t)dt F[ (t)]
	a

Пример.

1						x sin t;
	1 x 2 dx
0						0;			/ 2
	1			1				/ 2			1
			t			sin 2t						sin
	2			2					4		4
							0

	/ 2		/ 2	1	/ 2
		1 sin 2 t cos tdt cos 2 tdt			(1 cos 2t)dt
				2
	0	0			0

4 .

Пример.

x sin x

t sin t

sin t

sin t

I

0

dx

x t 0

dt

0

dt

0

dt

1 cos 2 x

1 cos 2 t

1 cos 2 t

1 cos 2 t

sin t

I

0

dt

1 cos 2 t

x sin x

dx

sin t

arctg cos t

2

Следовательно, I

dt

01 cos 2 x

2 01 cos 2 t

2

0

4

Пример.

ln

1 x

4

2 sin

I

dx x tg

ln 1 tg d

tg

4

1

1 x2

cos

0

0

4

4

4

во втором интеграле

ln

2d

ln cos d

ln sin

d

0

0

4

0

4

4

4

ln 2

ln 2

ln sin

d

ln sin

d

8

0

4

0

4

8

При замене переменной в определенном интеграле следует помнить о том, что вводимая функция должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.

Пример.

dx x

,

с

другой

стороны,

если применить

тригонометрическую

0

0

подстановку,

dx

dx

0

dt

dx

tgx t

0

sin

2

x cos

2

cos

2

x(1 tg

2

1

2

0

0

x

0

x)

0

t

Т.е. два способа нахождения интеграла дают различные результаты. Это произошло

из-за того, что не был учтен тот факт,

что введенная переменная

tg x

имеет на отрезке

интегрирования разрыв (в точке

x 2 ).

Поэтому в данном

случае

такая подстановка

неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.

Важные примеры. Рассмотрим интеграл

a

1) f x dx , где f x нечётная на a, a функция

a

Имеем

28

a

0

a

во первом интеграле

a

a

f x dx

f

x dx f

x dx

t

f t dt f x dx 0

a

a

0

x

0

0

Аналогично доказывается, что

a

f x dx

a

x dx , где

f x чётная на a, a функция

2

f

a

0

a T

T

f x периодическая функция с периодом

2

Докажем,

что f x dx

f x dx , где

a

0

T

Действительно

a T

0

T

a T

в ттретье

интеграле

f x dx

f x dx f x dx

f x dx

a

a

0

T

x t T

0

T

0

T

f x dx f

x dx f

x dx f

x dx

a

0

a

0

Интегрирование по частям.

Если функции u x и v x

непрерывны на отрезке a,b , а также непрерывны

на этом отрезке их производные, то справедлива формула интегрирования по частям:

b

b

udv uv

b vdu.

a

a

a

Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше, поэтому здесь приводить его нет смысла.

Пример.

		2	n
	I n
			sin xdx, I n
		0

	2
	cos n xdx,	n N
	0

Рассмотрим первый интеграл и проинтегрируем его по частям

		2														2
	I n sin n 1 xd cos x sin n 1 x cos x														2 n 1		sin n 2 x cos 2 xdx
		0													0		0
									2							2
	cos 2 x 1 sin 2 x n 1										sin n 2 xdx n 1						sin n xdx n 1 I n 2 n 1 I n
										0						0
	Следовательно,			I n	n 1				I n 2
						n
	Пусть n 2k , тогда
		2	,		1							1 3				2k 1 !!
	I0	dx		I 2				, I 2						,	I 2k
																2k !! 2
					2 2							2 4 2
		0	2
	При n 2k 1 имеем
		2					2					2 4				2k !!
	I1	sin xdx 1, I3						,		I5			,		I 2k 1
																2k 1 !!
		0			3							3 5

	получаются аналогичные результаты.
Упражнение: показать, что для I n

arctgx
Пример. Вычислить интеграл I		dx .
	1 x
0

Применим формулу интегрирования по частям

29

arctgx					ln 1 x
		dx arctgxd ln x 1 arctgx ln x 1		0				dx arctg ln 1		ln 2
0 1 x		0			0 1 x2				8

	n		2		n
				cos n x sin nxdx,
Пример. I					I
			0

	2
	cos n x cos nxdx,	n N
	0

Рассмотрим первый интеграл. Проинтегрируем его по частям

						2								2												2
												n								n		cos n x cos nxdx		0
I									cos n x sin nxdx			1				cos n xd cos nxdx				1					2		cos n 1 x sin x cos nxdx
	n
						0					0															0
			1				2
								cos n 1 x sin x cos nxdx
			n
								0
Прибавим к обеим частям по I n , получим
							2								2											2
														n								n	cos n x cos nxdx		0
2I										cos n x sin nxdx			1				cos n xd cos nxdx					1			2					cos n 1 x sin x cos nxdx
			n
									0							0												0
			1				2											1		2								1
										cos n 1 x sin x cos nx cos x sin nx dx												cos n 1 x sin n 1 x dx									I
			n															n											n			n 1
								0												0
Откуда находим
						1			1
I n											I n 1
						2
									n

По этой рекуррентной формуле можно окончательно получить

					1			2		22		22					2n
I	n																			(Доказать самостоятельно)
					n 1
				2				1		2		3
																		n
Аналогично находим, что
I
	n			2n 1
										1
Пример.								I ,n x lnn xdx,										n N , 0
										0
Интегрирование почастям даёт
					1								1			1					x 1		1		n		1
I ,n x lnn xdx																lnn xdx				1		lnn x					x lnn 1
													1												1
					0											0					1		0				0

	xdx	n		I ,n 1
		1

Откуда получается

I ,n

n

I ,n 1 n

n!

I ,n 1

1

1 n 1

1

dx

Пример. Вычислить интеграл

e x 1 x2 1

1

Сделаем замену переменной x tgt,

dx

dt

, тогда

cos 2 t

1

dx

4

dt

4

e tgtdt

I

e x 1 x2

1

etgt 1

e tgt 1

1

4

4

С другой стороны

30