Лекции по Матанализу ч

4		dt				4		1			e			tgt			e					tgt						4		e	tgt				t z					4	e	tgz
																							dt											dt									dz
		etgt 1									etgt																			etgt
							4												1					2								1			dt dz			2			e tgz 1
4																												4												4
		4			e tgz
										dz								I
	2	4 e tgz 1													2
Сравнивая с предыдущим результатом, получаем ревенство
	I I
2
											1										dx							4		dt
											1 e x 1 x2 1																4 etgt 1								4
Следовательно,							I
Упражнения. Доказать формулы
2															1
cos n x sin n 2 x							dx											,
0													n		1
2
cos n x cos n 2 x dx 0,
0
2													sin			n
sinn x cos n 2 x							dx										2				,
0														n 1
2												cos				n
sinn x sin n 2 x dx																	2				, n N
0														n 1

Докажем, например, формулу 2. Для этого рассмотрим вспомогательный интеграл

2

cos n 2 x cos n 2 x dx

0

И проинтегрируем его по частям дважды

				2				x cos n 2 x dx				1	2			xd sin n 2 x			1					x sin n 2 x		2
I	n 2					cos n 2									cos n 2						cos n 2
												n 2								n 2						0
				0										0
		2										1	2									1									2
		cos n 1 x sin x sin n 2 x dx												cos n 1 x sin xd cos n 2 x										cos n 1 x sin x cos n 2 x
												n 2										n 2
		0												0																	0
		1		2													n 1 2										1
				n 1 cos n x sin2 x cos n 2 x cos n												2 x d x			cos n x sin2					x cos n 2 x d x					I n 2
		n 2															n 2											n 2
				0															0
sin2				x 1 cos 2 x					n 1	2
											cos n x cos n 2 x d x I
									n 2							n 2
										0
Таким образом, получено, что
					n 1		2
I								cosn x cos n 2 x d x I
	n 2				n 2									n 2
						0
								2
откуда следует, что								cosn x cos n 2 x d x
								0

31

Приближенное вычисление определенного интеграла.

Как было сказано выше, существует огромное количество функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подинтегральная функция заменяется “близкой” к ней функцией, интеграл от которой выражается через элементарные функции.

Формула прямоугольников.

Если известны значения функции f(x) в некоторых точках x0, x1, … , xm, то в качестве функции “близкой” к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.

	b	b
	f (x)dx P(x)dx
	a	a
	Если разбить отрезок интегрирования на n равных частей x		b a	. При этом:
			n
	y0 = f(x0),	y1 = f(x1), …. , yn = f(xn).
	Составим суммы: y0 x + y1 x + … + yn-1 x
	y1 x + y2 x + … + yn x

Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной.

b		b a
Тогда f (x)dx				( y0	y1	... yn 1 ) или
		n
a
b		b a
f (x)dx				( y1	y2	... yn ) - любая из этих формул может применяться
		n
a

для приближенного вычисления определенного интеграла и называется общей формулой

прямоугольников.

	Формула трапеций.
	Эта формула является более точной по
у	сравнению с формулой прямоугольников.
	Подинтегральная функция в этом случае
	заменяется на вписанную ломаную.

y1		у2		уn
a	x1 x2		b	x

Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.

Площади вписанных трапеций вычисляются по формулам:

y0 y1

x;

y1 y2

x;

... ,

yn 1 yn

x

2

2

2

b

y1 y2

yn 1 yn

f (x)dx

y0 y1

x

x ...

x

a

2

2

2

32

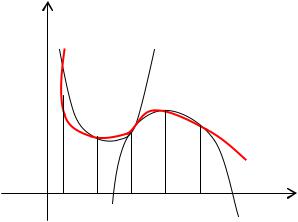
После приведения подобных слагаемых получаем формулу трапеций:

b	b a y				y
f (x)dx				0		n	y1 y2	... yn 1
a	n				2

Формула парабол (формула Симпсона или квадратурная формула). (Томас Симпсон (1710-1761)- английский математик)

Разделим отрезок интегрирования [a, b] на четное число отрезков (2m). Площадь криволинейной трапеции, ограниченной графиком функции f(x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями f(x0), f(x1), f(x2).

Для каждой пары отрезков построим такую параболу.

у

0 х0 х1

х2 х3

х4

х

Уравнения этих парабол имеют вид Ax2 + Bx + C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.

y

0

Ax 2

Bx

0

C

0

y

Ax 2

Bx

C

(1)

1

1

1

y

2

Ax 2

Bx

2

C

2

Обозначим 2h x2

x0 .

x2

x

3

x

2

x2

S ( Ax 2 Bx C)dx

A

B

Cx

x

3

2

x0

0

Если принять х0=-h, x1= 0, x2 = h, то S

h

(2Ah 2

6C)

(2)

3

Тогда уравнения значений функции (1) имеют вид:

y

0

Ah 2

Bh C

y1 C

y

2

Ah 2

Bh C

C учетом этого: y

0

4y

y

2

2Ah2 6C .

1

Отсюда уравнение (2) примет вид:

S

h

( y

4 y

y

)

0

2

3

1

Тогда

33

x
2	f (x)dx	h	( y0	4 y1 y2 )
x0	3
x
2	f (x)dx	h	( y2	4 y3 y4 )
x2	3

...............................................

Складывая эти выражения, получаем формулу Симпсона:

b
f (x)dx b a y0 y2m 2( y2 y4 ... y2m 2 ) 4( y1 y3 ... y2m 1 )
a	6m

Чем больше взять число m, тем более точное значение интеграла будет получено.

						8
Пример. Вычислить приближенное значение определенного интеграла							x3 16dx
						2
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей.
По формуле Симпсона получим:
8			8 2
	x3 16dx			[ y( 2) y(8)	2[ y(0) y(2) y(4)	y(6)]
2			6 5

4[ y( 1) y(1) y(3) y(5) y(7)]].

m	0			1				2		3	4	5	6	7	8	9	10
x	-2			-1				0		1	2	3	4	5	6	7	8
f(x)	2.828			3.873				4		4.123	4.899	6.557	8.944	11.874	15.232	18.947	22.978
	8					8		2
	x3		16dx						[2.828 22.978 2[4 4.899 8.944 15.232]
							6 5
	2
	4[3.873 4.123							6.557 11.874 18.947]] 91.151

Точное значение этого интеграла – 91.173.

Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.

Для сравнения применим к этой же задаче формулу трапеций.

	8			b a y				y						8 2		2.828 22.978
		x3 16dx					0		n	y1 y2	... yn 1						3.873	4	4.123
	2			n				2						10		2

4.899 6.557 8.944 11.874 15.232 18.947) 91.352

Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.

34

Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур.

у

+		+
0 a	-	b	x

Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

b

Для нахождения суммарной площади используется формула S f (x)dx .

a

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.

	6
	5
	4
	3
	2
	1
- 1	1	2	3	4
	- 1

Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:

2	2		x	3		x	2	2				8		4		1		1		5
S x2 dx xdx																					(ед2)
1	1		3		2					1		3	2		3		2		6

35

Нахождение площади криволинейного сектора.

= f( )

О

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид= f( ), где - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а - угол наклона этого радиус – вектора к полярной оси.

Площадь криволинейного сектора может быть найдена по формуле

S 1 f 2 ( )d

2

Вычисление длины дуги кривой.

y

y = f(x)

Si yixi

a

b

x

Длина ломаной линии, которая соответствует дуге, может быть найдена как

n

Sn Si .

i 1

n

Тогда длина дуги равна S lim Si .

max Si 0 i 1

2

2

2

yi

Из геометрических соображений: Si

xi

yi

1

xi

xi

В то же время yi

f (xi ) f (xi 1 )

xi

xi

Тогда можно показать (см. Интегрируемая функция.), что

n

b

dy

2

Si

S lim

1

dx

max xi 0

i 1

a

dx

b

Т.е. S 1 f (x) 2 dx

a

36

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем

S 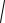(t) 2 (t) 2 dt ,

где х = (t) и у = (t).

Если задана пространственная кривая, и х = (t), у = (t) и z = Z(t), то

S (t) 2 (t) 2 Z (t) 2 dt

Если кривая задана в полярных координатах, то

S	2 2 d ,		= f( ).

Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2. 1 способ. Выразим из уравнения переменную у. y r 2 x2

Найдем производную y

x

r 2

x2

r

r

1

x2

r

x

r

Тогда

S

1

dx

dx r arcsin

r

2

x

2

4

r

r 2 x2

r 0

2

0

0

Тогда S = 2 r. Получили общеизвестную формулу длины окружности.

2 способ. Если представить заданное уравнение в полярной системе координат, то

	получим: r2cos2 + r2sin2 = r2, т.е. функция = f( ) = r,			df ( )	0	тогда
				d
	2		2
	S	0 r 2 d r d 2 r
	0	0

Вычисление объемов тел.

Вычисление объема тела по известным площадям его параллельных сечений.

S(xi-1)

S(xi)

a	xi-1	xi	b	x
Пусть имеется тело объема V . Площадь любого			поперечного сечения тела S ,
известна как непрерывная	функция	S S x . Разобьем	тело на “слои”	поперечными

сечениями, проходящими через точки хi разбиения отрезка a,b . Т.к. на какомлибо промежуточном отрезке разбиения xi 1 , xi функция S x непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M i и mi .

37

Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны

M i xi	и mi xi , где	xi xi xi 1 .
	Произведя	такие построения		для всех отрезков разбиения, и просуммировав
			n		n
полученные объёмы, получим M i xi					и mi xi .
			i 1		i 1
	При стремлении к нулю шага разбиения , эти суммы имеют общий предел:
			n			n	b
		lim	M i xi		lim	mi xi	Q(x)dx
		0	i 1		0	i 1	a

Таким образом, объем тела может быть найден по формуле:

b

V Q(x)dx

a

Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию S x , что весьма проблематично для сложных тел.

Пример: Найти объем шара радиуса R .

y

R y

-R

0

x R

x

В поперечных сечениях шара получаются окружности переменного радиуса у. В

зависимости от текущей координаты х этот радиус выражается по формуле

R2 x2 .Тогда

функция площадей сечений имеет вид:

x R2 x2 .

S

Получаем объем шара:

3

R

3

3

3

R

x

R

R

4 R

V

(R2

x2 )dx (R2 x

)

R3

R3

.

3

3

3

R

R

3

Пример: Найти объем произвольной пирамиды с высотой H и площадью основания

Sо .

S x Sо

x

H

x

При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x H , где x – расстояние от плоскости сечения до вершины пирамиды.

38

Из геометрии известно, что отношение площадей подобных фигур равно

коэффициенту подобия в квадрате, т.е.

S x

x

2

Sо

H

Отсюда получаем функцию площадей сечений: S(x)

Sо

x2 .

H 2

H

Sо

2

Sо x3

H

1

Находим объем пирамиды: V

dx

0

x

Sо H

H 2

3H 2

3

0

Объем тел вращения.

Рассмотрим кривую,

заданную уравнением y f x . Предположим, что функция

f x непрерывна на отрезке

a,b . Если соответствующую ей криволинейную трапецию с

основаниями a и b вращать вокруг оси Ox , то получим так называемое тело вращения. y f x

x

Т.к. каждое сечение тела плоскостью x const представляет собой круг радиуса R f (x) , то объем тела вращения может быть легко найден по полученной выше формуле:

b

V f 2 (x)dx

a

Площадь поверхности тела вращения.

Мi B

А

х

xi

Определение:	Площадью поверхности вращения кривой AB вокруг данной оси
называют предел, к	которому стремятся площади поверхностей вращения ломаных,
	39

вписанных в кривую AB , при стремлении к нулю наибольших из длин звеньев этих ломаных.

Разобьем дугу AB на n частей точками M 0 A, M1 , , M n 1 , M n B . Координаты вершин полученной ломаной имеют координаты xi и yi . При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна Pi . Эта площадь может быть найдена по формуле:

P 2

yi 1 yi

S

i

i

2

Здесь Si – длина каждой хорды.

y

2

2

2

i

Si xi

yi

1

xi

xi

Применяем теорему Лагранжа к отношению

yi

.Получаем:

xi

yi

f (xi ) f (xi 1 )

f (

),

x

x

i

i 1

i

xi

xi xi 1

Тогда

yi 1 yi

Si

1 f 2 ( i ) xi

Pi

2

1 f 2 ( i ) xi

2

Площадь поверхности, описанной ломаной равна:

		n
		Pn f (xi 1 ) f (xi ) 1 f 2 ( i ) xi
		i 1
Эта сумма не является интегральной, но можно показать, что
		n					n
P	lim f (xi 1 ) f (xi )		1 f 2 ( i ) xi			lim 2 f ( i )		1 f 2 ( i ) xi
	max xi 0	i 1				max xi 0	i 1

Тогда

b

P 2 f (x)1 f 2 (x)dx

a

- формула вычисления площади поверхности тела вращения.

40