Вычисление несобственных интегралов.

      ~           ~       

 

Утверждение. Пусть R(x, y) - рациональная функция двух действительных переменных. Тогда справедливы равенства

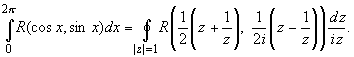
Действительно, замена z = e^ix переводит отрезок      в окружность |z| = 1, . При этом:  

В результате имеем формулу, сопоставляющую интеграл от действительной переменной с интегралом по замкнутой кривой от функции комплексного переменного:  

Замечание. Для вычисления таких интегралов в математическом анализе в общем случае, за исключением некоторых частных случаев, применяется замена tg(1/2)= t ("универсальная" подстановка) и интеграл приводится к интегралу от рациональной дроби.

 

Утверждение. Пусть функция   где P_n(x) и Q_m(x) - многочлены степени n и m (n = const, m = const), удовлетворяет условиям: 1. (m - n) больше или равно 2. 2. Q_m(x) не равна 0 при x, принадлежащим области действительных чисел. Тогда справедливы равенства: Здесь z_k, k = 1,2,..., p - все особые точки функции R(z), расположенные выше оси Ох (Im z_k> 0) в случае формулы (1) и ниже оси Ох (Im z_k< 0) в случае формулы (1.2).

 

Замечание. Если R(z) - четная функция, то можно, используя формулы (1.1) и (1.2), вычислить интеграл вида   т.к. для четной функции имеет место равенство:   

Утверждение. Пусть R(x) - рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, - нуль порядка не ниже первого (т.е. (m - n) больше или равно 1). Тогда справедливы формулы:

Преобразования Лапласа. Решение задач Коши операционным методом.

Операционное исчисление - один из наиболее эффективных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. При решении операционным методом задача интегрирования линейного дифференциального уравнения с постоянными коэффициентами сводится к задаче о решении алгебраического уравнения.

Функцией-оригиналом называется функция  f (x) для которой справедливо: f (x) непрерывна при неотрицательных x, за исключением, быть может конечного числа точек, f (x) = 0 при x<0, существуют такие постоянные M и a, что при всех неотрицательных x.

Преобразованием Лапласа функции f (x) называется функция

Функция F (p) называется изображением функции f (x), а функция f (x) - оригиналом для F (p).

 

Основные свойства преобразования Лаплалса, используемые при решении дифференциальных уравнений следующие:

• оригинал восстанавливется по изображению единственным образом, с точностью до значений в точках разрыва - теорема единственности;

• если F (p) и G (p) - изображения соответственно для f (x) и g (x), то изображением для af (x) + bg (x) является aF (p) + bG (p) - линейность преобразования Лапласа;

• изображением для производной f ⁽ⁿ⁾(x) является функция pⁿF(p) - p^n-1f (0) - p^n-2f '(0) -...-  pf ^(n-2)(0) - f ^(n-1)(0) - изображение производных;

• если F (p) изображения для f (x), то для любого a>0 изображением для f (x-a) является  - теорема запаздывания.

Рассмотри задачу Коши: a₁, a₂, ..., a_n - постоянные.

 

Алгоритм решения задачи Коши для уравнений операционным методом состоит в следующем. Обрзначим Y (p) и F (p) изображения для y (x) и f (x). Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим: или, A (p)Y (p) + B (p) = F (p), где A (p) и B (p) - многочлены. Отсюда: и искомое решение задачи Коши y (x) является оригиналом для Y (p).

 

Совершенно аналогично операционное исчисление применяется к решению задачи Коши для систем линейных дифференциальных уравнений с постоянными коэффициентами. Рассмотри задачу Коши: A- постоянна матрица размерности n.n.

 

Алгоритм решения задачи Коши для систем операционным методом состоит в следующем. Обозначим изображения для - компонентами вектор-функций являются изображения соответствующих компонент вектор-функций . Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим: , где E - единичная матрица, - обратная матрица к матрице. Тогда искомое решение задачи Коши является оригиналом для .