2.2. Характеристическое уравнение.

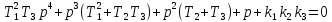
2.3. Проверка устойчивости системы по критерию Рауса-Гурвица.

Возьмем характеристический полином:

Составим из коэффициентов этого полинома определитель:

Этот определитель имеет n строк и n столбцов. В главной диагонали оказываются последовательно все коэффициенты, кроме a₀.

Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.

Характеристический полином:

Определяем коэффициенты характеристического уравнения:

В условия устойчивости в качестве их части входит требование положительности всех коэффициентов уравнения (необходимое условие устойчивости). Анализ устойчивости надо начинать с проверки этого простого необходимого, но недостаточного условия устойчивости. При его невыполнении, естественно, отпадает надобность в составлении и проверке остальных неравенств.

Следовательно, так как а₀ > 0, а₁ > 0, а₂ > 0, а₃ > 0, а₄ > 0 – необходимое условие выполняется.

Составим матрицу из коэффициентов характеристического полинома:

=

Для выполнения условия устойчивости необходимо и достаточно, чтобы все диагональные миноры были положительными (помимо того, что все коэффициенты a_0÷ a₄ положительны).

;

Определим диагональные миноры матрицы:

;

∆₁> 0, ∆₂ > 0, ∆₃ > 0, ∆₄ > 0 – достаточное условие выполняется.

Все определители матрицы Рауса-Гурвица и коэффициенты a_i получились больше нуля, поэтому можно сделать вывод, что система по критерию Рауса-Гурвица устойчива.

2.4. Проверка устойчивости системы по критерию Михайлова.

Об устойчивости замкнутой системы регулирования судят по виду кривой Михайлова, представляющей собой годограф вектора, представляющей собой годограф вектора α(jω).

Критерий Михайлова формулируется так: система устойчива, если годограф A(jω), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы.

Изобразим A(jω) в виде годографа в комплексной плоскости. Этот годограф называется годографом Михайлова.

Уравнения α(jω) получается подстановкой в левую часть характеристического уравнения jω вместо р.

Кривая Михайлова строится на комплексной плоскости (по оси абсцисс откладываются действительные числа, по оси ординат – мнимые).

Представим уравнение α(jω) в виде действительной и мнимой частей:

Подставляя значения ω от 0 до ∞, получаем значения Y(ω).

Необходимо подставить такие значения, чтобы кривая была построена во всех четырех квадрантах комплексной плоскости.

1. ω =0 с^-1, X(ω) = 0,1∙0,2∙8 = 0,16

Y(ω) = 0

2. ω =0,25с^-1, X(ω) = 0,6²∙0,03∙0,25⁴ - (0,4 +0,03) ∙ 0,25² + 0,1∙0,2∙8 = 0,1332

Y(ω) = 0,25 – (0,6²+ 0,4∙0,03) ∙ 0,25³ = 0.2268

3. ω =0,5с^-1, X(ω) = 0,6²∙0,03∙0,5⁴ - (0,4 +0,03) ∙ 0,5² + 0,1∙0,2∙8 = 0,0532

Y(ω) = 0,5 – (0,6²+ 0,4∙0,03) ∙ 0,5³ = 0.407

4. ω =0,768с ^-1, X(ω) = 0,6²∙0,03∙0,768⁴ - (0,4 +0,03) ∙ 0,768² + 0,1∙0,2∙8 = -0,899

Y(ω) = 0,768 – (0,6²+ 0,4∙0,03) ∙ 0,768³ = 0.5486

5. ω =0,90 с^-1, X(ω) = 0,6²∙0,03∙0,9⁴ - (0,4 +0,03) ∙ 0,9² + 0,1∙0,2∙8 = -0.1812

Y(ω) = 0,90 – (0,6²+ 0,4∙0,03) ∙ 0,90³ = 0.5987

6. ω =1,5с^-1, X(ω) = 0,6²∙0,03∙1,5⁴ - (0,4 +0,03) ∙ 1,5² + 0,1∙0,2∙8 = -0.7528

Y(ω) = 1,5 – (0,6²+ 0,4∙0,03) ∙ 1,5³ = 0.663

7. ω =2,437^-1, X(ω) = 0,6²∙0,03∙2,437⁴ - (0,4 +0,03) ∙ 2,437² + 0,1∙0,2∙8

= -2.0128

Y(ω) = 2,437 – (0,6²+ 0,4∙0,03) ∙ 2,437 ³ = 0.2277

8. ω =3с^-1, X(ω) = 0,6²∙0,03∙3⁴ - (0,4 +0,03) ∙ 3² + 0,1∙0,2∙8 = -2.8352

Y(ω) = 3 – (0,6²+ 0,4∙0,03) ∙ 3³ = -0.348

9. ω =4 с^-1, X(ω) = 0,6²∙0,03∙4⁴ - (0,4 +0,03) ∙ 4² + 0,1∙0,2∙8 == -3.9552

Y(ω) = 4 – (0,6²+ 0,4∙0,03) ∙ 4 ³ = -1.952

10. ω =6с^-1, X(ω) = 0,6²∙0,03∙6⁴ - (0,4 +0,03) ∙ 6² + 0,1∙0,2∙8 = -1.3232

Y(ω) = 6 – (0,6²+ 0,4∙0,03) ∙ 6³ = -7.392

11. ω =7с^-1, X(ω) = 0,6²∙0,03∙7⁴ - (0,4 +0,03) ∙ 7² + 0,1∙0,2∙8 = 5.0208

Y(ω) = 7 – (0,6²+ 0,4∙0,03) ∙ 7³ = -11.228

12. ω =8,522с^-1, X(ω) = 0,6²∙0,03∙8,522⁴ - (0,4 +0,03) ∙ 8,522² + 0,1∙0,2∙8 = 25.8941

Y(ω) = 8,522 – (0,6²+ 0,4∙0,03) ∙ 8,522³ = -18.4943

Найдем точки пересечения годографа вектора частотной функции А(j) с осями на комплексной плоскости:

a) с j; 0,0108 ∙⁴ - 0,43∙ ² + 0,16 = 0

₁ = 0,613; ₂ = 6,28

при ₁ j₁= ₁- 0,372∙₁³ = 0,613 – 0,372∙0,613³ = 0,5273

при ₂ j₂= ₂- 0,372∙₂³ = 6,28 -0,372∙6,28³ = -85.8544

б) с “+1; -1”. - 0,372³= 0

₃= 0; ₄= 2,44;

при ₃ “+1” = 0,0108 ∙ ⁴ - 0,43∙ 0 ² + 0,16 = 0.16

при ₄ “-1” = 0,0108 ∙ ⁴ - 0,43 ∙ ² + 0,16 = -2.0172.

Занесем рассчитанные данные в таблицу 2.

Таблица 2.

ω,l/c	0	0,25	0,5	0,768	0,9	1,5	2,437	3	4	6	7	8,522
X(ω)	0,16	0,133	0,053	-0,899	-0.181	-0.753	-2.013	-2.835	-3.955	-1.323	5.021	25.894
Y(ω)	0	0.227	0.407	0.549	0.599	0.663	0.228	-0.348	-1.952	-7.392	-11.228	-18.494

Рис.3. Годограф Михайлова по исследованию устойчивости САР с n=4

Вывод: Годограф последовательно проходит четыре квадранта. Годограф берет свое начало из точки 0,16, находящейся на действительной положительной полуоси и проходит последовательно против часовой стрелки 4 квадранта. Следовательно, по критерию Михайлова система устойчива.