MU_samostoyatelnoy_rabote

трапеции ≈	≈		+	( − )
			2

Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования).

Метод парабол (Симпсона)

Суть метода парабол заключается в приближении функции на отрезке [a,b] интерполяционным многочленном второй степени p2(x), т.е. приближение графика функции на отрезке параболой. В методе Симпсона для вычисления определенного интеграла весь интервал интегрирования [a,b] разбивается на подинтервалы равной длины h=(b-a)/2N. Число отрезков разбиения 2N должно быть четным числом.

			Симпсона ≈	≈
	≈		0 + 4 1 + 3 + + 2−1	+ 2( 2 + 4 + + 2−2)+ 2
		3

y0,y2N- сумма первого и последнего значения подынтегральной функции;

(y2 + y4 + + y2N−2) - сумма членов с чётными индексами умножается на

2;

y1 + y3 + + y2N−1	-сумма членов с нечётными индексами умножается на
4.
		Пример
Вычислить интеграл	методами:	прямоугольников, трапеции и параболы
(Симпсона).
	2
	3 − 2	1 − = 5.25
	−1

31

Разобьем отрезок [-1,2] на 10 частей, т.е. = 2−10(−1) = 0.3 . Вычислим

значение интеграла по формулам левых, правых, средних прямоугольников, по формуле трапеций и формуле Симпсона. Для этого составим таблицы:

						Таблица 3.1
					i				( )			( + +1)			( + +1)
												2			2
					0		-1		4			-0.85			4.213375
					1	-0.7			4.267			-0.55			4.181125
					2	-0.4			3.976			-0.25			3.671875
					3	-0.1			3.289			0.05			2.847625
					4	0.2			2.368			0.35			1.870375
					5	0.5			1.375			0.65			0.902125
					6	0.8			0.472			0.95			0.104875
					7	1.1			-0.179			1.25			-0.359375
					8	1.4			-0.416			1.55			-0.328625
					9	1.7			-0.077			1.85			0.359125
					10		2		1
	=				(			) = 4 + 4.267 + +							−0.077	= 19.075
1						−1
				=1
	=				( ) = 4.267 + 3.976 + + −0.077											= 16.075
2
		=1					+ )
				((
=					−1					= 4.213375 + + 0.359125 = 17.4625
3						2

=1

Формула левых, правых и средних прямоугольников:

	≈	≈	(	) = 0.3 19.075 = 5.7225
левых			−1
			=1

	≈	≈	( ) = 0.3 16.075 = 4.8225
правых
			=1

32

≈

≈

(

+ ) = 0.3 17.4625 = 5.23875

средних

−1

=1

−1

+

≈

≈

−1

=

трапеции

2

=1

+

−1

=

0

+

( )

2

=1

= 0.3

4 + 1

+ 4.2.67 + 3.976 + + (−0.077) = 5.2725

2

Симпсона ≈

≈

3

≈

0 + 4 1 + 3 + + 2−1

+ 2( 2 + 4 + + 2−2)+ 2 ≈

3

0.3 ≈ 3 4 + 4 4.267 + 3.289 + 1.375 − 0.179 − 0.077

+ 2 3.976 + 2.368 + 0.472 − 0.416 + 1 ≈ 5.25

Численное дифференцирование

Метод Эйлера

Дифференциальным называется уравнение, содержащее один или несколько производных. В зависимости от количества не зависимых переменных, дифференциальные уравнения делятся на две категории.

1)Обыкновенные дифференциальные уравнения (ОДУ)

2)Дифференциальные уравнения в частных производных. Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции . Их можно записать виде

( , ′ , ", … ( )) = 0

(1)

( )независимая переменная Наивысший порядок , входящий в уравнение (1) называется порядком

дифференциального уравнения.

33

Простейшим (линейным) ОДУ является уравнение (1) разрешенное

относительно производной
′ = ,	(2)
Решением дифференциального уравнения (1) называется всякая	функция,

= которая после ее подстановки в уравнение обращает его в тождество.

Основная задача, связанная с линейной ОДУ известно как задача

Каши: найти решение уравнения (2) в виде функции		удовлетворяющий
начальному условию ( 0) = 0		(3)
Геометрически это означает, что требуется найти интегральную
кривую,	проходящую через точку ( 0, 0) при выполнение равенства
(2).

Численный с точки зрения задачи Каши означает: требуется построить таблицу значений функции удовлетворяющий уравнение (2) и начальное условие (3) на отрезке ; с некоторым шагом 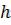. Обычно считается, что

0 = то есть начальное условие задано в левом конце отрезка.

Простейшим из численных методов решения дифференциального уравнения является метод Эйлера. В его основе лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме или таблицы.

Пусть дано уравнение ′ = , с начальным условием ( 0) = 0 то есть поставлена задача Каши. Решим вначале следующую задачу. Найти простейшим способом приближенное значение решения в некоторой точке1 = 0 + где -достаточно малый шаг. Уравнение (2) совместно с

начальным условием (3) задают направление касательной искомой интегральной кривой в точке 0 с координатами ( 0, 0)

Уравнение касательной имеет вид

= 0 + 0, 0 ( − 0)

Двигаясь	вдоль этой касательной,	получим приближенное значение
решения в точке 1:
	1 = 0 + 0, 0	1 − 0
или
	1 = 0 + · 0, 0		(4)
Располагая	приближенным решением в точке		1( 1, 1) можно

повторить описанную ранее процедуру: построить прямую проходящую через эту точку с угловым коэффициентом ( 1, 1), и по ней найти приближенное значение решения в точке 1 = 1 + .

Заметим, что эта прямая не является касательной к реальной интегральной кривой, поскольку точка 1 нам не доступна, однако если

достаточно мало то получаемые приближенные будут близки к точным значениям решения.

34

Продолжая эту идею, построим систему равно отстоящих точек

= 0 + · = 0, .

Получение таблицы значений искомой функции по методу Эйлера заключается в циклическом применение формулы

	=	+ ∆ =		+ · ( , )	(5)
+1

Рисунок. 1. Геометрическая иллюстрация метода Эйлера
Решение	ОДУ	в некоторой точке xi называется	устойчивым,	если
найденное в	этой	точке значение функции yi мало	изменяется	при

уменьшении шага интегрирования. Для проверки устойчивости, таким

образом, надо провести два расчета				значения (yi) – с		шагом
интегрирования 2h и при уменьшенной (например,					двое) величине шага. В
качестве	критерия	устойчивости	можно		использовать	малость
относительного изменения полученного			решения		при уменьшении шага
интегрирования

= 2 −

2

где 2 - решение, рассчитанное с шагом 2h , – решение, рассчитанное с шагом h .

Пример

В качестве примера проведем расчеты по формулам метода Эйлера с

шагом h=0,05 и h=0,1 для задачи Коши ′						= −2 , 0 < < 1, 0 = 1.
Формулы для расчета имеют вид 0 = 0,
				= +
			+1
	= − 2 =				1 − 2 ;		= 0,1,2,3 … . ,
+1

35

Рассчитываем с шагом h = 0.1
0.	0 = 1
1.	1 = 0		1 − 2 0 0	= 1 1 − 2 0 1 0.1 = 1
2.	2 = 1		1 − 2 1 1	= 1 1 − 2 0.1 1 0.1 = 0.98
3.	3 = 2		1 − 2 2 2	= 0.98 1 − 2 0.2 0.98 0.1 = 0.94
***
10. 10 = 9 1 − 2 9 9 = 0.3817
Рассчитываем с шагом h = 0.05
0.	0 = 1
1.	1	= 0	1 − 2 0 0	= 1 1 − 2 0 1 0.05 = 1
2.	2	= 1	1 − 2 1 1	= 1 1 − 2 0.05 1 0.05 = 0.995
3.	3	= 2	1 − 2 2 2	= 0,995 1 − 2 0.1 0,995 0.05 = 0.985

***
20. 10. 20 = 19 1 − 2 19 19							= 0.3743
Точное решение имеет вид = −2
				1			= 0.368
Относительное изменение полученного решения
=	2 −			=		0.3817 − 0.3743			= 0.019
		2					0.3817
Относительная изменение составляет 1.9%
Относительная погрешность при шаге интегрирования h = 0.05
=		−	=		0.3817 − 0.368			= 0.035
							0.3817

составляет 3.5%

Листинг программы решение обыкновенного дифференциального уравнения методом Эйлера

Усовершенствованный метод Эйлера

Точность метода Эйлера можно повысить, если воспользоваться для аппроксимации интеграла более точной формулой интегрирования – формулой трапеций.

Основная идея этого метода: вычисляемое по формуле (5) очередное значение +1 = + · , будет точнее, если значение производной, то есть угловой коэффициент прямой замещающей интегральную кривую на

36

отрезке		,			будет вычисляться не по левому краю (то есть в точке ), а
			+1
по центру отрезка ,							. Но так как значение производной между точками
						+1
	и	не		вычисляется,			то перейдем к сдвоенным участкам	,
	+1						−1	+1

центром, в которых является точка , при этом уравнение прямой получает
вид:
	=	+ ,			· ( −	)	(6)
	−1				−1
А формула (5) получает вид
	= + ∆		=		+ 2 · ( , )		(7)
+1			−1

Формула (7) применена только для ≥ 1, следовательно, значения 1 по ней получить нельзя, поэтому находят по методу Эйлера, при этом для получения более точного результата поступают так: с начала по формуле (5) находят значение

							1	= 0 +		· 0, 0						(8)
						2		2
	В точке 1		= 0	+		, а затем находится 1					по формуле (7) с шагом
					2											2
		2
						1		= 0 + ∙				1	,	1		(9)
											2		2

После того как 1 найдено дальнейшие вычисления при = 1,2,3, … . , производится по формуле (7)

2 = 0 + 2 · 1, 1 ….

Пример

В качестве примера проведем расчеты по формулам усовершенствованного метода Эйлера с шагом h=0,1 для задачи Коши ′ = −2 , 0 < < 1, 0 = 1.

0 = 0;		0 = 1;
1	= 0	+		= 0 + 0.05 = 0.05
2		2
1 = 0		+ −2 0			0	= 1 + 0.1 0 = 1
2
1	= 0	+ −2 1			1	= 1 + 0.1 −2 0.05 1 = 0.99
		2			2
2	= 0	+ −2 1			1	= 1 + 0.1 −2 0.1 0.99 = 0.96

3 = 1 + 2	−2 2 2	= 0.99 + 2 0.1 −2 0.2 0.96	= 0.913
4 = 2 + 2	−2 3 3	= 0.96 + 2 0.1 −2 0.3 0.913	= 0.85
***
10 = 8 + 2	−2 9 9	= 0.3656

Точное решение имеет вид = −2

37

1 = 0.368

Относительная погрешность при шаге интегрирования h = 0.1 составляет 0.65%

= 1 − 10 = 0.368 − 0.3656 = 0.0065(1) 0.368

Модифицированный метод (Эйлера-Коши)

Повысить точность и устойчивость вычисления решения можно с

помощью неявного метода Эйлера следующего вида.
Прогноз:
	= + · ,					(10)
+1
Коррекция:
		=	+ ∙	, + +1, +1		(11)
+1					2

Геометрически это означает, что с начало определяется направление интегральной кривой в исходной точке ( , 1) и во вспомогательной точке+1, +1 , а в качестве окончательного направления берется среднее

значение этих направлений.

Благодаря более точной формуле интегрирования, погрешность метода пропорциональна уже квадрату шага интегрирования.

Пример

В качестве примера проведем расчеты по формулам модифицированным

методом Эйлера с шагом h=0,1	для задачи Коши ′ = −2 , 0 < <
1, 0 = 1.
1 = 0 + −2 0 0	= 1 + 0.1 −2 0 1 = 1

1 = 0 + 2 −2 0 0 + −2 1 1 = 1 + 0.05 0 + −2 0.1 1 = 0.99

2 = 1 + −2 1 1 = 0.99 + 0.1 −2 0.1 0.99 = 0.97

	2	= 1	+		−2 1 1	+ −2 2 2
				2

= 0.99 + 0.05 −2 0.1 0.99 + −2 0.2 0.97 = 0.961

38

Таблица Решение уравнения модифицированным методами Эйлера

xi	0	0.1	0.2	0.3		0.4			0.5	0.6		0.7	0.8	0.9	1.0
yi	1	0.99	0.961	0.914		0.852			0.779	0.698		0.613	0.528	0.446	0.369
Точное решение имеет вид = −2									1	= 0.368
	Относительная погрешность при шаге интегрирования h = 0.1
составляет 0.27%
			=	1 − 10			=	0.368 − 0.369				= 0.0027
				(1)					0.368

Метод Рунге-Кутты

Воспользовавшись хорошо зарекомендовавшей себя формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши для ОДУ первого порядка - широко используемого в вычислительной практике метода Рунге-Кутты.

В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [xi+1 , xi].

					1 = +
					+2		2
тогда можно определить так
						1+
				= +		+2	,
			+1
						1−
					+2
	= +		, + 4				,			+	,
+1		6			+ 2				+ 2	+1	+1

Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции yi+h/2 и yi+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений + 2, +1.

+1 = + 6 , + 4 + 2, + 2 + +1, +1

При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.

39

Алгоритм Рунге-Кутты четвертого порядка - (погрешность порядка h4):

		= +				1			+ 2 + 2						+
						6
+1								0		1				2			3
где
					0	= ,
				=				+				, +	0
										2				2
		1
				= +								, +	1
										2				2
			2

															3		= + , +												2
Алгоритм четвертого																	порядка					требует				на каждом								шаге			четырех
вычислений функции соответственно, но является весьма точным.
																					Пример
Используя алгоритм Рунге-Кутты																					четвертого					порядка решить задачу Коши
′ = −2 ,				0 < < 1,									0					= 1 с шагом h=0.1
																					0 = 0
										0		= 0, 0 = 0.1 −2 0 1																			= 0
			=							+			,		+			0		= 0.1 −2					0 +			0.1				1 + 0				= −0.01
											2																	2
			1				0							0			2
			= +							,		+		1			= 0.1 −2 0 +								0.1			1 +					−0.01			= −0.00995
							2							2																		2
	2			0						0																2
			3 = 0				+ , 0							+ 2 = 0.01 −2 0.1 (1 − 0.00995)																					= −0.0198
				= +	1						+ 2						+ 2				+	= 1 +		0 + 2 1 + 2 2 + 3												= 0.99
					6
			1	0						0					1					2	3										6
Результаты расчета сведены в таблицу
			0	0,1						0.2							0.3				0.4		0.5			0.6						0.7			0.8		0.9	1.0
			1	0.99			0.961								0.914						0.852		0.779			0.698					0.613				0.527		0.445	0.368
0			0	-0.02			-0.038							-0.055						-0.068			-0.078			-0.084					-0.086			-0.084			-0.08	-0.074
1			-0.01	-0.029			-0.047								-0.062						-0.074		-0.081			-0.085					-0.085				-0.082		-0.077	-0.07
2			-9.95x	-0.029			-0.047								-0.062						-0.073		-0.081			-0.085					-0.085				-0.083		-0.077	-0.07
			x10-3
3			-0.02	-0.038			-0.055								-0.068						-0.078		-0.084			-0.086					-0.084				-0.08		-0.074	-0.066

Относительная погрешность при шаге интегрирования h = 0.1 составляет 0.00%

40