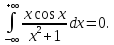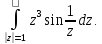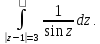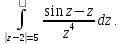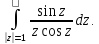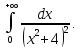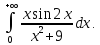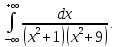Вступительный экзамен 2018 / Раздел 17 (ответы)
.docxРаздел 17. Вычеты. Вычисление интегралов с помощью вычетов.
Вычислить:
Особые точки
подынтегральной функции:
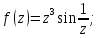
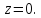
Контур
интегрирования
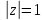 представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
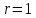 .
.
Особая точка
подынтегральной функции
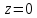 принадлежит области, ограниченной
контуром интегрирования. Тогда:
принадлежит области, ограниченной
контуром интегрирования. Тогда:

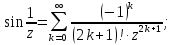
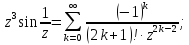
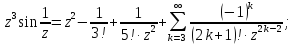
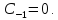
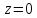 – существенно особая точка, т.к. главная
часть ряда Лорана в окрестности этой
точки содержит бесконечное число членов.
– существенно особая точка, т.к. главная
часть ряда Лорана в окрестности этой
точки содержит бесконечное число членов.
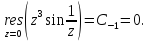
Тогда искомый
интеграл равен
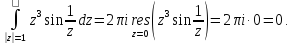
Ответ:
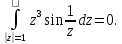
Особые точки
подынтегральной функции:


Контур
интегрирования
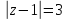 представляет из себя окружность на
комплексной плоскости с центром в точке
представляет из себя окружность на
комплексной плоскости с центром в точке
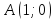 и радиусом
и радиусом
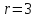 .
.
Особые точки
подынтегральной функции
 принадлежат области, ограниченной
контуром интегрирования. Тогда:
принадлежат области, ограниченной
контуром интегрирования. Тогда:
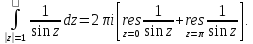
Определим
тип особых точек
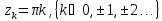
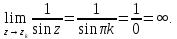
 – полюса функции, определим их порядок.
– полюса функции, определим их порядок.
Порядок
полюсов
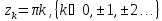 для функции
для функции
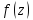 равен порядку нулей
равен порядку нулей
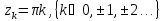 для
функции
для
функции
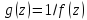
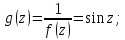
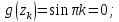
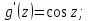

Для функции
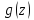 точки
точки
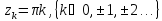 –
нули первого порядка. Таким образом для
функции
–
нули первого порядка. Таким образом для
функции
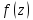 точки
точки
 простые полюса.
простые полюса.
Вычет для простого полюса найдем по формуле:
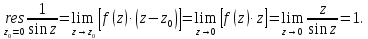
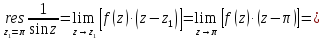
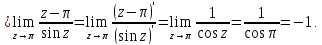
Тогда искомый интеграл равен:
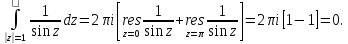
Ответ: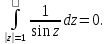
Особые точки
подынтегральной функции:
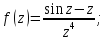
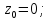
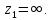
Контур
интегрирования
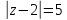 представляет из себя окружность на
комплексной плоскости с центром в точке
представляет из себя окружность на
комплексной плоскости с центром в точке
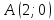 и радиусом
и радиусом
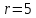 .
.
Особая точки
подынтегральной функции
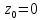 принадлежат области, ограниченной
контуром интегрирования. Тогда:
принадлежат области, ограниченной
контуром интегрирования. Тогда:
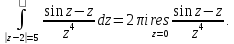
Определим
тип особой точки
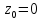 .
Воспользуемся разложением в ряд Лорана:
.
Воспользуемся разложением в ряд Лорана:

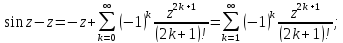
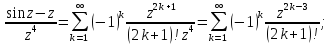
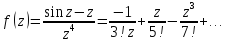
Точка
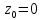 является простым полюсом, так как номер
старшего члена главной части ряда Лорана
функции в ее разложении в окрестности
точки равен единице.
является простым полюсом, так как номер
старшего члена главной части ряда Лорана
функции в ее разложении в окрестности
точки равен единице.
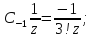
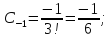
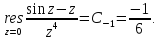
Тогда искомый интеграл равен
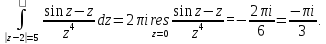
Ответ: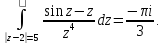
Особые точки
подынтегральной функции:
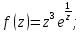
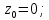
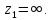
Контур
интегрирования
 представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
 .
.
Особая точки
подынтегральной функции
 принадлежат области, ограниченной
контуром интегрирования. Тогда:
принадлежат области, ограниченной
контуром интегрирования. Тогда:
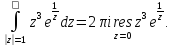
Определим
тип особой точки
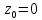 .
Воспользуемся разложением в ряд Лорана:
.
Воспользуемся разложением в ряд Лорана:
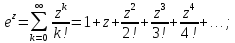
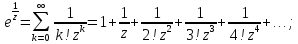
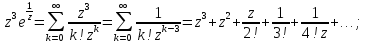
Точка
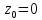 является существенно особой точкой,
так как главная часть ряда Лорана функции
в ее разложении в окрестности точки
содержит бесконечное число членов.
является существенно особой точкой,
так как главная часть ряда Лорана функции
в ее разложении в окрестности точки
содержит бесконечное число членов.
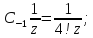
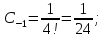

Тогда искомый интеграл равен
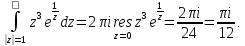
Ответ:

Найдем особые
точки подынтегральной функции:
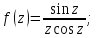
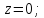
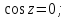
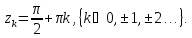
Контур
интегрирования
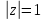 представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
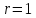 .
.
Особая точка
подынтегральной функции
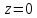 принадлежат области, ограниченной
контуром интегрирования. Тогда:
принадлежат области, ограниченной
контуром интегрирования. Тогда:
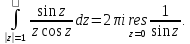
Определим
тип особой точки
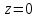
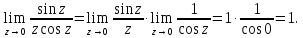
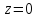 – устранимая особая точка.
– устранимая особая точка.
Вычет в устранимой особой точке равен:
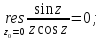
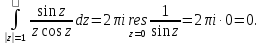
Ответ:
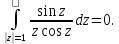
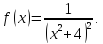
Подынтегральная
функция представляет из себя частное
двух многочленов, со степенью числителя
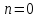 и степенью знаменателя
и степенью знаменателя
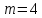 .
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
.
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
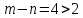 ,
то справедливо равенство:
,
то справедливо равенство:

где
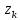 – особые точки функции
– особые точки функции
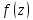 ,
расположенные выше оси Ox.
,
расположенные выше оси Ox.
Найдем особые точки функции

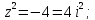
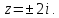
Выше оси Ох
расположена одна особая точка
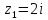 ,
определим ее тип:
,
определим ее тип:

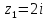 – полюс функции. Определим его порядок.
Для того чтоб точка
– полюс функции. Определим его порядок.
Для того чтоб точка
 была полюсом порядка n
функции
была полюсом порядка n
функции
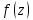 ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
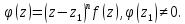
Тогда
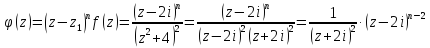
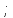

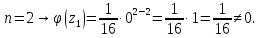
Таким образом,
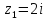 – полюс второго порядка.
– полюс второго порядка.
Вычет для полюса второго порядка определим по формуле:
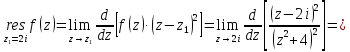
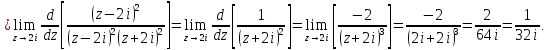
Тогда искомый интеграл равен
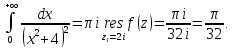
Ответ:

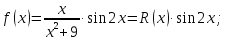
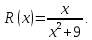
Функция
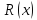 представляет из себя частное двух
многочленов, со степенью числителя
представляет из себя частное двух
многочленов, со степенью числителя
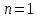 и степенью знаменателя
и степенью знаменателя
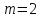 .
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
.
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
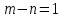 ,
то справедливо равенство:
,
то справедливо равенство:
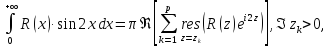
где
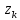 – особые точки функции
– особые точки функции
 ,
расположенные выше оси Ox.
,
расположенные выше оси Ox.
Найдем
особые точки функции
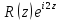 :
:
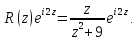
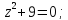
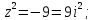
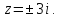
Выше
оси Ох расположена одна особая точка
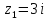 ,
определим ее тип:
,
определим ее тип:
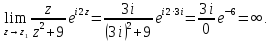
 – полюс функции.
Определим его порядок. Для того чтоб
точка
– полюс функции.
Определим его порядок. Для того чтоб
точка
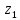 была полюсом порядка n
функции
была полюсом порядка n
функции
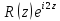 ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
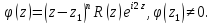
Тогда

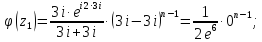

Таким
образом,
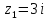 – простой полюс.
– простой полюс.
Вычет для простого полюса определим по формуле:

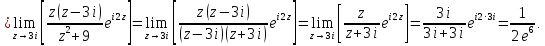
Тогда искомый интеграл равен
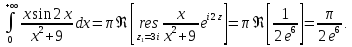
Ответ:
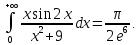
Перейдем от интеграла от действительной переменной к интегралу по замкнутой кривой от функции комплексного переменного:
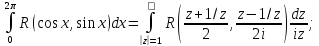
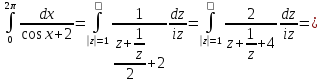
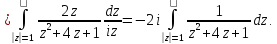
Найдем особые точки подынтегральной функции:
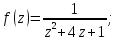
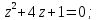
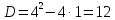
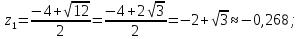

Контур
интегрирования
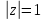 представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
представляет из себя окружность на
комплексной плоскости с центром в начале
координат и радиусом
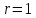 .
.
Особая точка
подынтегральной функции
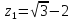 принадлежат области, ограниченной
контуром интегрирования. Тогда:
принадлежат области, ограниченной
контуром интегрирования. Тогда:
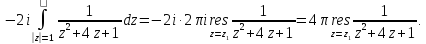
Так как для
функции
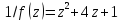 точка
точка
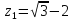 нуль первого порядка, то для функции
нуль первого порядка, то для функции
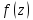 точка
точка
 – простой полюс.
– простой полюс.
Вычет для простого полюса определим по формуле:
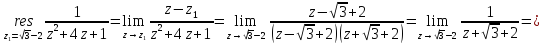
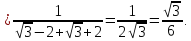
Тогда искомый интеграл равен
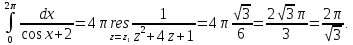
Ответ:

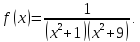
Подынтегральная
функция представляет из себя частное
двух многочленов, со степенью числителя
 и степенью знаменателя
и степенью знаменателя
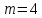 .
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
.
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
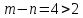 ,
то справедливо равенство:
,
то справедливо равенство:
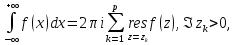
где
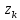 – особые точки функции
– особые точки функции
 ,
расположенные выше оси Ox.
,
расположенные выше оси Ox.
Найдем особые точки функции
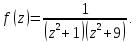
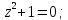
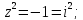
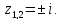

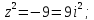
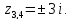
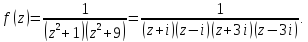
Выше оси Ох
расположены две особые точки
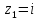 и
и
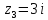 ,
определим их тип:
,
определим их тип:
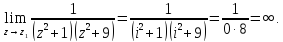
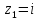 – полюс функции.
– полюс функции.
Так как для
функции
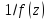 точка
точка
 нуль первого порядка, то для функции
нуль первого порядка, то для функции
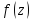 точка
точка
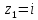 – простой полюс.
– простой полюс.
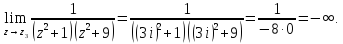
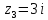 – полюс функции.
– полюс функции.
Так как для
функции
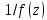 точка
точка
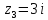 нуль первого порядка, то для функции
нуль первого порядка, то для функции
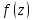 точка
точка
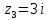 – простой полюс.
– простой полюс.
Вычет для простых полюсов определим по формуле:
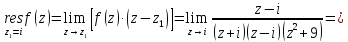
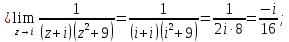
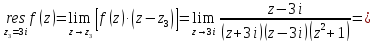

Тогда искомый интеграл равен
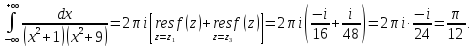
Ответ:

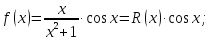
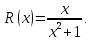
Функция
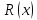 представляет из себя частное двух
многочленов, со степенью числителя
представляет из себя частное двух
многочленов, со степенью числителя
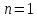 и степенью знаменателя
и степенью знаменателя
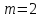 .
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
.
Так как подынтегральная функция не
имеет особых точек на действительной
оси и
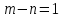 ,
то справедливо равенство:
,
то справедливо равенство:

где
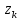 – особые точки функции
– особые точки функции
 ,
расположенные выше оси Ox.
,
расположенные выше оси Ox.
Найдем особые
точки функции
 :
:
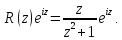
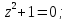
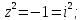

Выше оси Ох
расположена одна особая точка
 ,
определим ее тип:
,
определим ее тип:
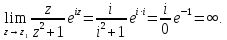
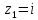 – полюс функции. Определим его порядок.
Для того чтоб точка
– полюс функции. Определим его порядок.
Для того чтоб точка
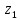 была полюсом порядка n
функции
была полюсом порядка n
функции
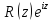 ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
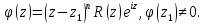
Тогда
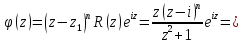
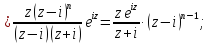
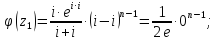
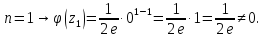
Таким образом,
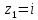 – простой полюс.
– простой полюс.
Вычет для простого полюса определим по формуле:
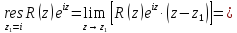
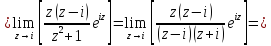
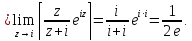
Тогда искомый интеграл равен

Ответ: