Весна 16 курс 3 ОрТОР / Гидравлика / lektsia__5

5. 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ЭЙЛЕРА

Дифференциальные уравнения равновесия жидкости впервые опубликованы Эйлером в 1755 году и выведены для общего случая, когда на жидкость действуют не только сила тяжести, но и другие массовые силы, например, силы инерции переносного движения при относительном покое, а также сила давления.

В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом W с ребрами dx ,dy, dz, расположенными параллельно осям координат х, у и z.

D

А O B

C

 

Рис. 5.1.1.

На выделенный объем действуют две силы – сила тяжести, направленная вниз и сила давления жидкости на грани параллелепипеда.

Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на ускорение свободного падения g, т.е. равна gdm. Сила гидростатического давления на любую из граней параллелепипеда равна произведению гидростатического давления р на площадь этой грани. Будем считать, что давление р является функцией всех трех координат: p =f(х, y,z).

Масса жидкости, находящейся в элементарном параллелепипеде,

dm = ρdxdydz.

Проекции массовых сил в направлении координатных осей

dF_mx =Xdm =Xρdxdydz;

dF_my =Ydm = Yρdxdydz;

dF_mz = Zdm= Zρdxdydz,

где X, Y, Z – компоненты единичных массовых сил относительно осей x, y, z.

Точки А и В находятся в центрах тяжести левой и правой граней параллелепипеда. Эти центры получены в результате проведения через центральную точку О горизонтальной линии. Давление в точке А равно p_А в точке В - p_в.

Гидростатическое давление изменяется непрерывно линейно и приращение давления на единицу длины по координатным осям составляет: по dx приращение , по dy - dy и по dz - dz.

Гидростатическое давление в точках А и В отличается от давления p в центре тяжести в параллелепипеде О на величину dx.

Давление в точках А и В

p_А =p - dx;

p_в =p + dx.

Так как площади граней бесконечно малы, то давления p_А и p_В можно считать средними гидростатическими давлениями по этим граням (площадкам).

Поверхностные силы определяются гидростатическим давлением, приходящимся на соответствующие грани параллелепипеда.

Поверхностные силы давления на левой и правой гранях по оси x равны произведению давления на площади граней

dF_XА = p_Аdydz = dydz;

dF_Xв = p_Вdydz = dydz.

Аналогично можно определить силы давления на грани по оси z

dF_ZC = p_Сdxdy = dxdy;

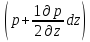dF_ZD = p_Ddxdy =dxdy.

Таким же образом определяются силы гидростатического давления по оси y.

Уравнение равновесия жидкости, находящейся в элементарном параллелепипеде, соблюдается, когда сумма всех сил, действующих на данный объём, по всем осям x, y, z будет равна нулю.

Составим уравнение равновесия поверхностных и массовых сил, действующих по осям x, y и z

dF_XА - dF_XВ + dF_mx = 0;

dF_ZС - dF_ZD + dF_mz = O.

Или

dydz – +Xρdxdydz = 0;

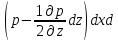y –dxdy + Zρdxdydz = 0.

После преобразования последних уравнений и разделив уравнения на ρdxdydz, получим

X- = 0;

Z - = 0.

Аналогичное уравнение можно получить относительно оси y

Y - = 0.

Тогда получим систему уравнений

X- = 0;

Y - = 0;

Z - = 0.

Полученные уравнения являются дифференциальными уравнениями равновесия жидкости - уравнениями Эйлера.

Умножив каждое уравнение соответственно на dx, dy, dz будем иметь следующую систему уравнений

Xdx - dx = 0;

Ydy - dy =0;

Zdz - dz = 0.

Сложим все члены системы уравнений

dx +dy +dz = ρ

Полный дифференциал давления

dp = dx + dy +dz.

Следовательно полный дифференциал давления выражается через массовые силы

dp = ρ

Последнее уравнение является основным уравнением гидростатики в дифференциальной форме.

Полагаем, что рассматриваемая жидкость имеет постоянную плотность ρ = const, следовательно правая часть уравнения является дифференциалом некоторой функции U = f (x, y, z). Частные производные этой функции

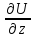= X, =Y, = Z.

Функция U называется потенциальной функцией, а силы, которые выражаются этой функцией, являются силами, имеющими потенциал.

Таким образом, следует вывод, что жидкость может находиться в равновесии только под действием массовых сил, имеющих потенциал.

Введём в уравнение полного дифференциала давления функцию U

dx +dy+dz =dp

или

du = dp.

5.2. ПОВЕРХНОСТИ РАВНОГО ДАВЛЕНИЯ

Поверхность жидкости, во всех точках которой давление одинаково, называется поверхностью равного давления.

Уравнение свободной поверхности можно получить из уравнения полного дифференциала давления, считая ρ = const и p = const; dp = 0, тогда

Xdx + Ydy + Zdz = 0

или через потенциальную функцию

U = f (x, y,z) = const.

Последнее уравнение является уравнением равновесия в дифференциальной форме.

Частички жидкости, находящиеся на поверхности равного давления, имеют одинаковую удельную потенциальную энергию, соответствующую действующим массовым силам.

Свободная поверхность жидкости, которая граничит с какой-либо газовой средой, является одной из поверхностей равного давления. В случае, когда поверхность соприкасается с воздушной средой, во всех её точках давление равно атмосферному давлению.

Как уже отмечалось ранее, на жидкость могут действовать как силы тяжести, так и силы инерции. Например, при неравномерном или непрямолинейном движении резервуара с жидкостью положение её уровня будет отличаться от случая, когда резервуар находится в неподвижном состоянии. Под действием инерционных сил, постоянных по времени, жидкость в резервуаре приобретает новое положение равновесия, т. е. она становится неподвижной относительно стенок резервуара. Жидкость в резервуаре, таким образом, будет находиться в относительном покое.

В случае нахождения жидкости в относительном покое равнодействующая массовых сил будет направлена по нормали к поверхности равного давления.

5.3. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ

УРАВНЕНИЙ РАВНОВЕСИЯ

при абсолютном и относительном покое жидкости

1. Жидкость находится в абсолютном покое в резервуаре, неподвиж-

ном относительно земли. На жидкость в резервуаре из массовых сил действует только сила тяжести (G =mg).

z p_о

p

h

z_о

z

о x

Рис.5.3.1.

y

На поверхность жидкости в резервуаре действует давление p_о. на рисунке ось z направлена вертикально вверх. Проекции единичных массовых сил на оси x и y будут равны: X =0, Y=0.

Проекция единичной силы на ось Z =-g, так как ось z направлена в сторону, противоположную силе тяжести mg.

После подстановки в уравнение полного дифференциал давления Z =-g получим дифференциал давления

dp =ρgdz.

В результате интегрирования будем иметь

p = -ρgz + С,

где С - постоянная интегрирования.

Для нахождения значения постоянной интегрирования С используем граничные условия. На свободной поверхности жидкости в резервуаре p = p_о при z = z_о, следовательно

С = p_о +ρgz.

Подставляем значение найденной постоянной интегрирования С в выражениеp

p =p_о + ρgz_о – ρgz

или

p = p_о +ρg = p_о +ρgh,

где h – глубина погружения плоскости относительно свободной поверхности.

Таким образом, используя основное дифференциальное уравнение гидростатики, пришли к последнему уравнению.

Характер поверхности равного давления определяется уравнением

Xdx +Ydy +Zdz = 0.

Для данного случая X = 0, Y= 0,Z = -g.

Следовательно

-gdz = 0.

Из полученного дифференциального уравнения следует, что z должна быть постоянной величиной, z =const.

Таким образом, поверхностью равного давления будет любая горизонтальная плоскость, расположенная ниже или по свободной поверхности в резервуаре. Поверхность равного давления при z = z_о, соприкасающаяся с атмосферной средой, называется свободной поверхностью.

2. Жидкость находится в относительном покое в резервуаре, который вместе с жидкостью движется прямолинейно равноускоренно. На жидкость в резервуаре, кроме силы тяжести, действует сила инерции (F = mа). На свободную поверхность действует давление p_о.

z

-x x

p_о

α x а

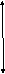
z_о z_о

α p

z x

z Рис. 5.3.2.

В данном случае единичная массовая сила инерции численно равна ускорению движения а резервуара с жидкостью и направлена в сторону, обратную движению. Следовательно,

X = - а, Y = 0, Z = - g.

Подставив в уравнение полного дифференциала давления единичные силы, получим

P = - ρadx– ρgdz.

После интегрирования

p =-ρаx-ρgz + С.

Постоянная интегрирования С определяется согласно граничным условиям, при x = 0 и z = z_о давление p = p_о.

Тогда

С = p_о + ρgz_о.

Следовательно

p = p_о – ρax- ρg

или разность давлений

p – p_о = ρgh – ρax.

Характер поверхности равного давления определяется дифференциальным уравнением.

Дифференциальное уравнение при X = -a, Y = 0, Z = - g принимает следующий вид:

- ax – gz = С.

Согласно граничным условиям x = 0, z = z_о получим

С = -gz_о, -ax + g=0.

Следовательно, координата свободной поверхности

z_оi = z_{о -} -x,

где z_оi – текущая координата поверхности.

Полученное уравнение показывает, что свободная поверхность в резервуаре представляет собой плоскость, наклеенную к горизонту под углом α.

Отношение ускорения a и g равно tg α = -.

Поверхности равного давления в жидкости будут представлять плоскости, параллельные свободной поверхности и находящиеся на равных глубинах погружения h.