ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Белгородский Государственный Технологический Университет

им. В.Г. Шухова

Институт информационных технологий и управляющих систем

Кафедра информационных технологий

Расчетно-графическое задание

На тему: «Численное интегрирование»

Вариант 1

Выполнила: ст. гр. ПЗ-11

Боганчикова Е. А.

Руководитель: ст. преп.

Кочеткова И. А.

Белгород 2011

Содержание.

1. Введение.

2. Теоретические сведения.

3. Задание к выполнению расчетно-графического задания.

4. Текст программы и блок-схема.

5. Сравнение между собой результатов и оценка погрешностей вычисления.

6. Заключение.

7. Список используемой литературы.

Введение.

В данном расчетно-графическом задании требуется применить изученные средства языка программирования Паскаль для решения задач путем использования численных методов интегрирования на компьютере.

Необходимо написать программу, решающую поставленную задачу, используя предоставленные математические данные. Решение данной задачи показывает возможности использования компьютера для различного рода прикладных вычислений.

В данной задаче требуется разработать алгоритм и его реализацию для нахождения интеграла функции с помощью метода прямоугольников, трапеций и формулы Симпсона. Ценность данной задачи заключается в том, что не для каждой функции значение интеграла можно найти аналитически. Однако с использованием предложенных численных методов, возможно, получить конкретное значение.

Теоретические сведения.

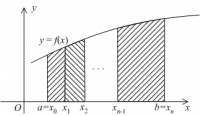
Рис.1

Задача численного интегрирования состоит в нахождении приближенного значения интеграла

( 1 )

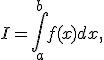
где  - заданная и интегрируемая на отрезке  функция.

Если один или оба предела равны  или , то с помощью трюков с заменой переменных можно осуществить переход к конечному отрезку от луча или всей числовой прямой.

Введем на  сетку с переменным шагом , т.е. множество точек , и представим интеграл (1) в виде суммы интегралов по частичным отрезкам:

( 3 )

Для построения формулы численного интегрирования на всем отрезке  достаточно построить квадратурную формулу для интеграла

( 4 )

на частичном отрезке  и воспользоваться свойством (3).

Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма  при стремлении всех промежутков ∆x_i к нулю

При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: 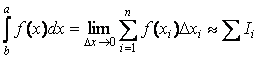, где I_i - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.

Метод прямоугольников

Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника

, где h - шаг интегрирования, у₀ - значение функции в точке х=х₀

у(х₀)=у₀

Рис.2 Численное интегрированние методом прямоугольников

Рис.3

Заменим интеграл ((3) выражением , где 

Тогда получим формулу

( 5 )

которая называется формулой прямоугольников на частичном отрезке 

Погрешность метода (5) определяется величиной

которую легко оценить с помощью формулы Тейлора. Действительно, запишем  в виде

( 6 )

и воспользуемся разложением

где . Тогда из (6) получим

Обозначая , оценим  следующим образом:

Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка

( 7 )

т.е. формула имеет погрешность  при .

Заметим,что оценка (7) является неулучшаемой, т.е. существует функция , для которой (7) выполняется со знаком равенства. Действительно, для  имеем  и

Составная формула прямоугольников и ее погрешность

Суммируя равенства (5) по  от  до , получим составную формулу прямоугольников

( 8 )

Погрешность этой формулы

равна сумме погрешностей по всем частичным отрезкам,

Отсюда, обозначая , получим

( 9 )

т.е. погрешность формулы прямоугольников на всем отрезке есть велицина .

Видим, что квадратурная формула имеет второй порядок точности.

Применимость метода к функции, заданной в конечном числе точек

Заметим, что метод прямоугольников в том виде,в котором он описан выше, не применим в общем случае к функциям,значения которых мы знаем в конечном числе точек, так как, например, мы не всегда можем разбить отрезкок интегрирования на подотрезки, серединами которых являются точки,в которых нам известно значение функции.

Метод трапеций.

Формула трапеций на частичном отрезке и ее погрешность

Рис.4

На частичном отрезке эта формула имеет вид

( 10 )

и получается путем замены подынтегральной функции  интерполяционным многочленом первой степени,постоенным по узлам , т.е. функцией

Для оценки погрешности достаточно вспомнить,что

Отсюда получим

и,следовательно,

( 11 )

Оценка (11) неулучшаема, так как в ней достигается равенство, например, для .

Составная формула трапеций и ее погрешность

Составная формула трапеций имеет вид

( 12 )

где .

Погрешность этой формулы оценивается следующим образом:

( 13 )

где 

Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности,, но ее погрешность оценивается величиной в два раза большей.

Применимость метода к функции, заданной в конечном числе точек

В отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как мы всегда можем взять в качестве узлов интегрирования данные точки.

Оценка погрешности

Величина погрешности численного интегрирования зависит как от шага сетки , так и от гладкости подынтегральной функции . Например, в оценку (11), наряду с , входит величина

которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке . Для этого прежде всего надо уметь апостериорно, т.е. после проведения расчета, оценивать погрешность.

Апостериорную оценку погрешности можно осуществить методом Рунге. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности , т.е. . Тогда

откуда получим

( 16 )

( 17 )

Пусть используется составная квадратурная формула

где  - квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций). Проведем на каждом частичном отрезке  все вычисления дважды, один раз - с шагом  и второй раз - с шагом  и оценим погрешность по правилу Рунге (17):

Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х₀,у₀) и (х₀+h,у₁), и вычисляем значение элемента интегральной суммы как площадь трапеции