§8. Центр системи паралельних сил і центр ваги твердого тіла. Геометричні характеристики плоских фігур.

8.1 Центр системи паралельних сил. Розглянемо систему паралельних сил спеціального виду, які мають один напрямок і фіксовані точки прикладання. Розв’яжемо першу задачу статики для заданої системи сил.

Нехай на тверде тіло діють сили , , , прикладені відповідно в точках А₁, А₂, А₃ і направлені в одну сторону (мал. 1.49).

Рівнодійна сил і має той же напрямок, що й і , дорівнює сумі величини складових сил , а точка прикладання належить відрізку А₁А₂ і із співвідношення

(1.53)

Аналогічно знаходимо рівнодійну сил і . Її величина дорівнює сумі величин сил і : , а точка прикладання С належить відрізку С₁ А₃ і задовольняє умову

(1.54)

Напрямок сили збігається з напрямком заданих сил.

Аналогічно можна знайти величину і точку прикладання рівнодійної довільного числа паралельних сил.

Штрихові лінії на мал. 1.49 показують, що положення точки прикладання рівнодійної не зміниться, якщо всі сили повернути відносно точок прикладання, залишаючи їх при цьому паралельними.

Точка С, в якій прикладена рівнодійна системи паралельних сил, називається її центром.

Визначимо координати центра паралельних сил , ,…, , прикладених в точках , , …, . Координати точки С позначимо через . Повернемо сили так, щоб вони стали паралельними осі Z (мал. 1.50). застосуємо до даної системи сил теорему Варіньона про момент рівнодійної відносно осей

; (1.55)

Звідки

; (1.56)

Якщо повернути сили так, щоб вони стали паралельними осі , то на підставі теореми Варіньона про момент рівнодійної відносно осі дістанемо

(1.57)

Формули (1.56)-(1.57) дозволяють визначати координати центра системи паралельних сил по заданих координатах точок їх прикладання.

8.2. Центр ваги твердого тіла. Будь-яке тверде тіло можна розглядати як сукупність великого числа маленьких частинок. На кожну з них діє направлена вертикально вниз (до центра Землі) сила тяжіння. Якщо розміри тіла малі в порівнянні з радіусом Землі, то сили тяжіння, що діють на частинки, можна вважати паралельними. Причому ці сили зберігають свою величину при довільних поворотах тіла (мал. 1.51).

Рівнодійна сил тяжіння всіх частин тіла дорівнює їх сумі і називається вагою тіла, а точка її прикладання С — центром ваги цього тіла. На підставі формул (1.56), (1.57) координати центра ваги у вибраній системі координат визначаються співвідношенням

; ; , (1.58)

де — координати точки прикладання сили тяжіння . Відзначимо, що згідно з означенням, центр ваги — геометрична точка, в окремих випадках вона може бути розміщена за межами тіла.

8.3. Координати центрів ваги однорідних тіл. Для однорідного тіла вага кожного його частини пропорціональна об’єму тіла, тобто , де γ — вага одиниці об’єкту.

Підставивши значення і у формули (1.58), знаходимо

; ; (1.59)

Точку С(), координати якої визначаються формулами (1.59), називають центром ваги тіла об’єкту V.

Якщо тверде тіло являє собою однорідну плоску і тонку пластинку, то врахувавши, що , із формул (1.58) знаходимо

(1.60)

де γ — вага одиниці площі пластини, — площа всієї пластини, а — площа її частин. Величини називаються координатами центра ваги площі плоскої фігури.

Аналогічно отримуємо формули для координат центра ваги лінії

; ; (1.61)

де L — довжина всієї лінії, — довжина її частин.

Як видно із формул (1.59) – (1.61), координати центра ваги однорідного тіла не залежать від його фізичних характеристик, а залежать лише від його геометричних параметрів.

Розглянемо основні методи визначення координат центрів ваги плоских фігур.

1) Симетрія. Якщо плоска фігура має вісь або центр геометричної симетрії, то її центр ваги лежить відповідно на осі або в центрі симетрії. Із властивостей симетричних фігур випливає, що в даному разі центр ваги круга, кільця, кола, паралелограма, прямокутника, квадрата розміщений в геометричному центрі.

2) Розбиття. Якщо тіло можна розбити на скінчене число фігур, для кожної з яких положення центра ваги відомо, то координати центра ваги складеної фігури обчислюються за формулами (1.60). якщо при цьому тіло має вирізи, то площа вирізаної частини приймається від’ємною.

На закінчення відзначимо, що центр ваги трикутника розміщений в точці перетину його медіан, а координати центрів ваги інших однорідних фігур можна знайти в різних технічних довідниках.

Приклад 5. Визначити положення центра ваги круглої пластинки радіусом з вирізом радіусом (мал. 1.52).

Розв’язування. Оскільки задана фігура має вісь симетрії, то центр ваги розміщений на осі . Для визначення координати зобразимо фігуру як суцільний круг радіусом додатної площі і круг радіусом від’ємної площі. При цьому

; ; ; .

Підставивши здобуті значення у формули (1.60), дістанемо

; .

Точка С розміщена лівіше від точки О.

8.4. Геометричні характеристики плоских фігур. Розглянемо плоску фігуру площею S, яка віднесена до прямокутної декартової системи координат (мал. 1.53).

Статичними моментами площі фігури відносно відповідних координатних осей називаються інтеграли виду

; , (1.62)

де — відстані від центра ваги елементарної площадки , до осей івідповідно. Розмірність статичного момента . Оскільки в більшості інженерних задач інтегрування можна замінити сумуванням шляхом розбиття фігури на частинки, для яких відомі площі і положення центрів ваги, то формули (1.62) можна подати у вигляді

; . (1.63)

Тут п — кількість частин фігури; S_i — площа частини фігури; — координати центра ваги частини фігури.

Урахувавши при цьому формули (1.60), знаходимо, що положення центра ваги плоскої фігури відносно вибраної системи координат, визначається співвідношенням

; (1.64)

Залежності (1.64) показують, що статичні моменти плоскої фігури відносно координатних осей, які проходять через центр ваги фігури, дорівнюють нулю.

Основними моментами інерції фігури відносно осей (мал. 1.53) називаються інтегралами виду

; (1.65)

Полярним моментом інерції фігури (мал. 1.53) називається інтеграл виду

, (1.66)

де ρ — відстань від центра елементарної площадки до початку системи координат (полюса).

Розмірність осьових і полярного моментів інерції фігури . Їх величина завжди додатна і не може дорівнювати нулю.

Урахувавши співвідношення , із (1.65), (1.66), дістанемо залежність

(1.67)

яка показує, що полярний момент інерції плоскої фігури дорівнює сумі осьових.

Відцентровим моментом інерції плоскої фігури (мал. 1.53) відносно осей називається інтеграл виду

(1.68)

Його розмірність така ж, як для осьових і полярного, але величина може бути додатною, від’ємною і дорівнювати нулю. Зокрема, якщо фігура симетрична хоча б відносно однієї з осей , то відцентровий момент відносно цих осей дорівнює нулю.

Координатні осі, що проходять через центр ваги фігури, і відцентровий момент відносно яких дорівнює нулю, називаються головними центральними осями.

Радіусом інерції і_х фігури відносно осі х називається величина, яка дорівнює , (1.69)

звідки .

Отже, момент інерції фігури відносно будь-якої осі дорівнює добутку площі її перерізу на квадрат радіуса інерції відносно цієї ж осі. Розмірність радіуса інерції — М. аналогічно визначаються полярний і відцентровий радіуси інерції.

Осьовим моментом опору фігури називається частка від ділення головного момента інерції на відстань від даної осі до найбільш віддалених від неї точок фігури

; , (1.70)

де — найбільші відстані від осей відповідно до точок фігури. Розмірність цієї величини — .

Величина називається полярним моментом опору ( — найбільша відстань від точок фігури до полюса).

Для ілюстрації сказаного вище розглянемо приклади визначення геометричних характеристик плоских фігур, які найчастіше зустрічаються на практиці.

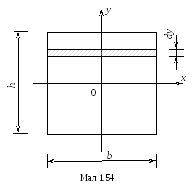Прямокутний переріз (мал. 1.54). Вважаємо, що координатні осі є головними і центральними . Виділимо елементарну площадку у вигляді смужки, паралельної осі х. Тоді на основі формул (1.65) дістанемо

.

Аналогічно обчислюємо . Полярний момент інерції знаходимо по формулі (1.67).

.

Підставляючи в (1.70) ; , матимемо вирази для осьових моментів опору прямокутника

; .

Знаючи момент інерції, за формулами (1.69) можна визначити відповідні радіуси інерції

; .

Круглий переріз (мал. 1.55). Нехай задана фігура віднесена до головних центральних осей . Для зручності елемент площі вибрано у вигляді кільця змінного радіуса ρ завтовшки ; площа цього кільця заштрихована на рисунку.

Полярний момент інерції круга, на підставі формули (1.66), дорівнює

.

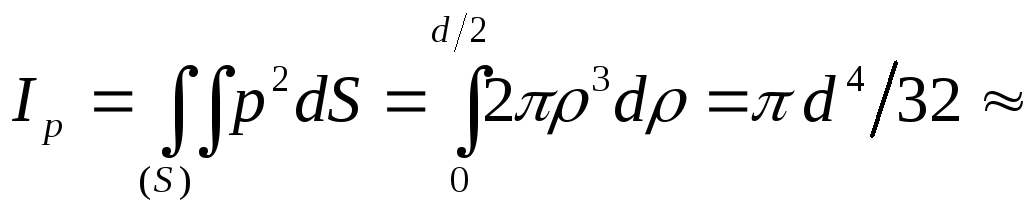
Осьові моменти інерції однакові, то, на підставі (1.67), дістанемо

Полярний момент опору обчислюємо за формулою

.

Зауважимо, що при заміні системи координат всі характеристики фігури не зміняться.

Геометричні характеристики інших плоских фігур приводяться у відповідних довідниках.