
- •Механіка суцільного середовища
- •Кінематика суцільного середовища
- •Основні поняття і задачі механіки суцільного середовища
- •Способи задання руху суцільного середовища
- •Розділ 2 елементи гідродинаміки
- •2.1. Основні поняття і формули векторного аналізу
- •2.2. Рівняння неперервності руху ідеальної рідини
- •2.3. Рівняння Ейлера
- •2.4. Гідростатика
- •2.5. Умова відсутності конвекції
- •2.6. Рівняння Бернуллі
- •Основи теорії пружності (теорія деформації)
- •3.1. Вектор зміщення і деформований стан
- •3.2. Тензор деформації
- •3.3. Перетворення компонент тензора деформації при заміні системи відліку
- •3.4. Головні напрямки тензора деформації. Головні осі і головні деформації
- •3.5. Визначення компонент вектора зміщення через компоненти тензора деформації
- •3.6. Визначення зміщень через компоненти тензора відносного зміщення
- •Основи теорії пружності (теорія напружень)
- •4.1 Зовнішні сили. Вектор напруження. Напружений стан тіла
- •4.2. Тензор напружень
- •4.3. Диференціальні рівняння рівноваги пружного тіла. Симетричність тензора напружень
- •4.4. Перетворення компонент тензора напружень при повороті системи координат
- •4.5. Головні напруження і інваріанти тензора напружень
- •Основи теорії пружності (співвідношення між компонентами тензора напружень)
- •5.1. Узагальнений закон Гука
- •Основи теорії пружності (основні рівняння і задачі теорії пружності)
- •6.1. Основні рівняння теорії пружності
- •6.2. Основні задачі статики пружного тіла
- •6.3. Пряма і обернена задачі теорії пружності
- •6.4. Рівняння пружної рівноваги в зміщеннях
- •6.5. Основні рівняння в напруженнях
- •Застосовуючи до (6.32) оператор Лапласа, одержимо
- •6.6. Напівобернений метод Сен-Венана
- •6.7. Принцип Сен-Венана
- •Найпростіші задачі теорії пружності
- •Метод суперпозиції
- •Основи теорії пружності (плоска задача теорії пружності)
- •7.1. Плоска деформація
- •7.2. Плоский напружений стан
- •7.3. Узагальнений плоский напружений стан
- •7.4. Основні рівняння плоскої теорії пружності. Зведення до бігармонічної проблеми
- •7.5. Плоска задача в декартових координатах
- •Нехай функція напружень має вигляд полінома третього степеня
- •Виберемо функцію напружень у вигляді полінома четвертого степеня
- •Якщо розглядається друга гранична задача, то граничні умови мають вигляд
- •8.2. Зведення основної задачі до бігармонічної проблеми
- •8.3. Задачі, в яких напруження залежать тільки від
- •Задачі, в яких напруження залежать від і
- •Підставляючи (8.67) у (8.64), одержимо формули для напружень
- •Застосування функцій комплексної змінної до розв’язування задач плоскої теорії пружності
- •9.1. Комплексне подання функції напружень
- •Розглянемо основне рівняння плоскої теорії пружності
- •9.2. Комплексне подання компонент тензора напружень і вектора зміщень
- •9.3. Степінь визначеності і структура комплексних потенціалів
- •9.4. Перетворення рівнянь плоскої задачі теорії пружності при конформному відображенні
- •9.5. Двосторонній розтяг нескінченної площини з еліптичним отвором
- •Список літератури
Якщо розглядається друга гранична задача, то граничні умови мають вигляд
![]() . (8.14)
. (8.14)
Тут
![]() – задані компоненти вектора зміщення;
– задані компоненти вектора зміщення;
![]() – контур області, яку займає тіло.
– контур області, яку займає тіло.
Умови сумісності Сен-Венана одержимо із (7.32) з урахуванням (8.10)
![]() , (8.15)
, (8.15)
де
![]() – оператор Лапласа в полярних координатах.
– оператор Лапласа в полярних координатах.
П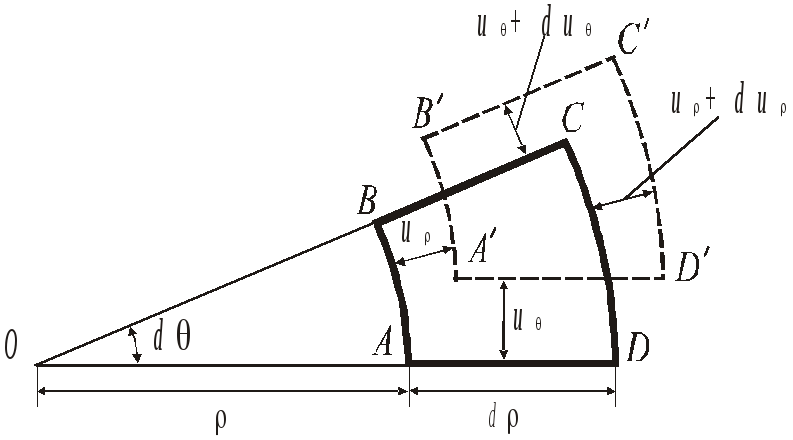 означимо
через
означимо
через
![]() і
і
![]() відносні видовження (деформації) у
напрямках
відносні видовження (деформації) у
напрямках
![]() і
і
![]() відповідно, а через
відповідно, а через
![]() відповідний кут зсуву між цими напрямками.
Для їх визначення розглянемо деформацію
елемента
відповідний кут зсуву між цими напрямками.
Для їх визначення розглянемо деформацію
елемента
![]() ,
утвореного двома парами координатних
ліній (рис. 8.5).
,
утвореного двома парами координатних
ліній (рис. 8.5).
С
Рис. 8.5![]() у радіальному напрямку одержить зміщення
у радіальному напрямку одержить зміщення
![]() ,
а сторона
,
а сторона
![]() –
–
![]() .
Тоді за означенням
.
Тоді за означенням
![]() . (8.16)
. (8.16)
Сторона
![]() змінює свою довжину за рахунок радіального
зміщення як дуга кола і за рахунок
видовження в напрямку
змінює свою довжину за рахунок радіального
зміщення як дуга кола і за рахунок
видовження в напрямку
![]() .
У першому випадку
.
У першому випадку
![]() ,
,
![]() ,
тому
,
тому
![]() .
.
В іншому випадку
![]() .
.
Додаючи останні два співвідношення, одержимо
![]() . (8.17)
. (8.17)
Допустимо,
що деформований елемент
![]() зміщений так, як показано на рис. 8.6. Зсув
прямого кута між сторонами
зміщений так, як показано на рис. 8.6. Зсув
прямого кута між сторонами
![]() і
і
![]() дорівнює сумі величин заштрихованих
кутів і визначається за формулою
дорівнює сумі величин заштрихованих
кутів і визначається за формулою
![]() . (8.18)
. (8.18)
При
виведенні останньої формули кути зсуву
замінені їх тангенсами і враховано, що
кут
![]() визначає поворот елемента
визначає поворот елемента
![]() як жорсткого цілого.
як жорсткого цілого.

Рис. 8.6
На підставі (8.16), (8.17), (8.18) диференціальні залежності Коші в полярних координатах можна записати у вигляді
![]() ;
;
![]() ;
;
![]() . (8.19)
. (8.19)
Для ізотропного матеріалу структура закону Гука не залежить від вибору системи координат, тому в полярних координатах цей закон в технічних сталих можна записати так:
![]() ;
;
![]() ;
;
![]() (8.20)
(8.20)
або
![]() ;
;
![]() ;
;
![]() . (8.21)
. (8.21)
8.2. Зведення основної задачі до бігармонічної проблеми
Основні рівняння плоскої теорії пружності у полярних координатах при відсутності масових сил на підставі п. 8.1 можна записати у вигляді:
диференціальні залежності Коші
![]() ;
;
![]() ;
;
![]() ; (8.22)
; (8.22)
умови сумісності Сен-Венана
![]() ; (8.23)
; (8.23)
диференціальні рівняння рівноваги
![]() ;
;
![]() ; (8.24)
; (8.24)
граничні умови
![]() ;
;
![]() при
при
![]() ;
;
![]() ;
;
![]() при
при
![]() ;
(8.25)
;
(8.25)
закон Гука
![]() ;
;
![]() ;
;
![]() . (8.26)
. (8.26)
Якщо
ввести функцію напружень
![]() за формулами
за формулами
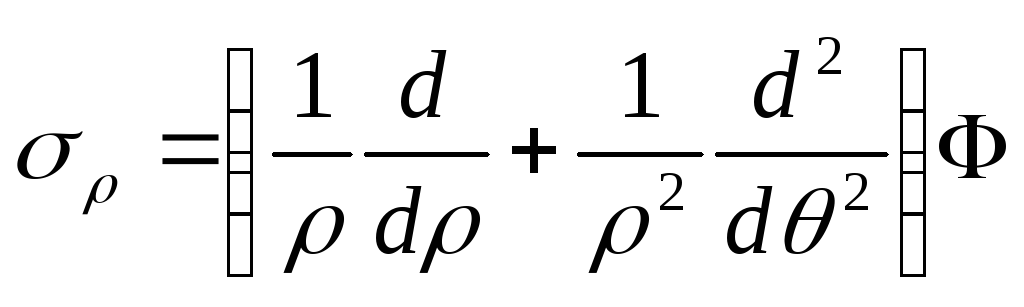 ;
;
![]() ;
;
![]() , (8.27)
, (8.27)
то рівняння рівноваги (8.24) будуть виконуватися тотожно. З умови сумісності (8.23) одержимо бігармонічне рівняння для визначення функції напружень
![]() . (8.28)
. (8.28)
Якщо розв’язок рівняння (8.28), який задовольняє граничним умовам
 ;
;
 при
при
![]() ;
;
![]() ;
;
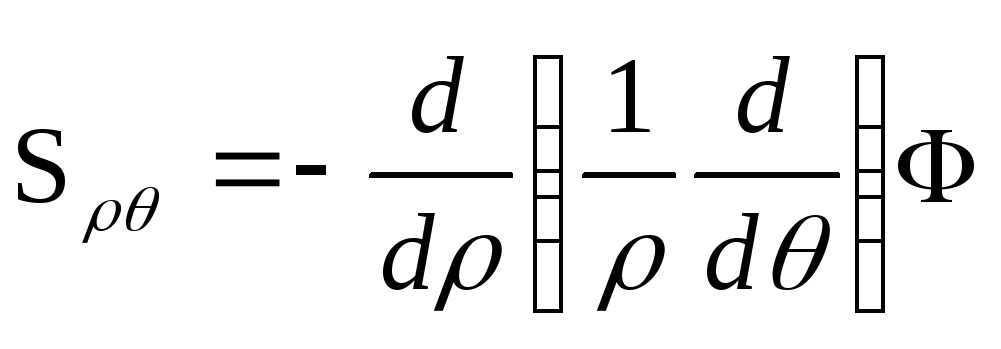 при
при
![]() , (8.29)
, (8.29)
буде відомим, то компоненти тензора напружень визначимо за формулами (8.27), а компоненти тензора деформації із співвідношень (8.21)
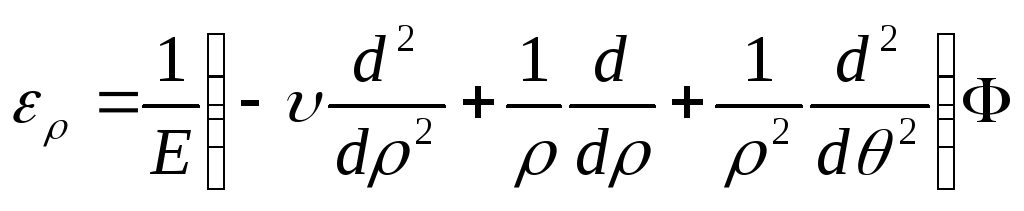 ;
;
 ;
;
![]() . (8.30)
. (8.30)
Для визначення компонент вектора зміщення необхідно проінтегрувати диференціальні залежності Коші (8.22).
8.3. Задачі, в яких напруження залежать тільки від
Для
деяких задач очевидна незалежність
компонент напруженого стану від полярного
кута
![]() .
У цьому випадку функцію напружень можна
подати у вигляді
.
У цьому випадку функцію напружень можна
подати у вигляді
![]() , (8.31)
, (8.31)
де
![]() – довільна стала;
– довільна стала;
![]() – функція, яка залежить тільки від
– функція, яка залежить тільки від
![]() .
.
Підставляючи
(8.31) в (8.28), знаходимо рівняння для
визначення
![]()
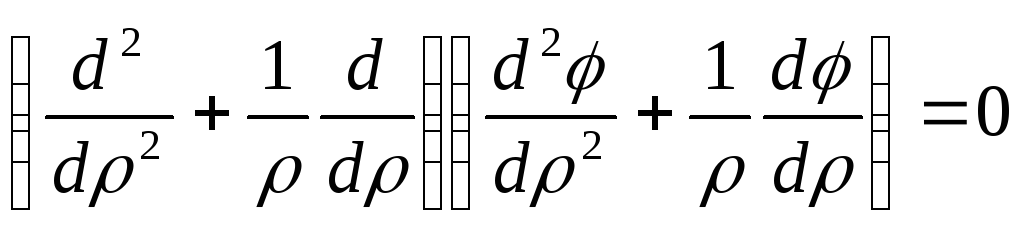 . (8.32)
. (8.32)
Враховуючи співвідношення
![]() ,
,
рівняння (8.32) подамо у вигляді
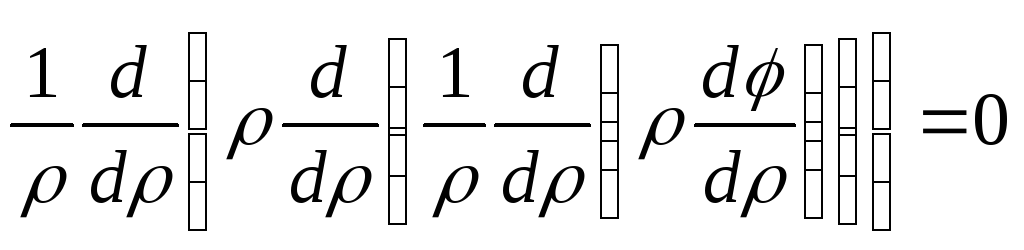 . (8.33)
. (8.33)
Після
чотирикратного інтегрування його по
![]() знаходимо
знаходимо
![]() . (8.34)
. (8.34)
Стала
![]() не впливає на напружений стан тіла, тому
на підставі (8.31) бігармонічна функція
має вигляд
не впливає на напружений стан тіла, тому
на підставі (8.31) бігармонічна функція
має вигляд
![]() . (8.35)
. (8.35)
Компоненти тензора напружень визначаємо за формулами (8.27)
![]() ;
;
![]() ;
;
![]() . (8.36)
. (8.36)
Компоненти тензора деформації у випадку плоского напруженого стану згідно з (8.22), (8.26) будуть визначатися співвідношеннями
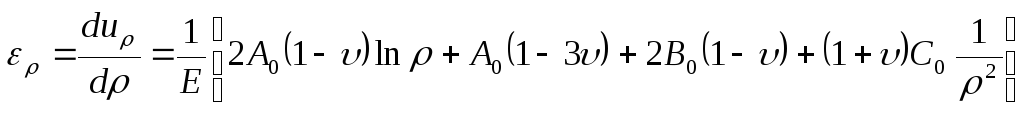 ;
;
![]()
![]() ;
;
![]() . (8.37)
. (8.37)
Інтегруючи
перше рівняння (8.37) по
![]() ,
визначаємо
,
визначаємо
![]()
![]() , (8.38)
, (8.38)
де
![]() – довільна функція аргумента
– довільна функція аргумента
![]() .
.
З другого рівняння (8.37), використовуючи (8.38), знаходимо
![]() . (8.39)
. (8.39)
Після
інтегрування (8.39) по
![]() ,
одержимо
,
одержимо
![]() . (8.40)
. (8.40)
Тут
![]() – довільна функція аргумента
– довільна функція аргумента
![]() .
.
Підставляючи (8.38), (8.40), у третє співвідношення (8.37), одержимо
![]() . (8.41)
. (8.41)
Остання рівність можлива тільки тоді, коли
![]() ;
;
![]() . (8.42)
. (8.42)
Розв’язуючи рівняння (8.42), знаходимо
![]() ;
;
![]() (8.43)
(8.43)
і формули (8.38), (8.40) для визначення компонент вектора зміщення приймають вигляд
![]()
![]() ;
;
![]() , (8.44)
, (8.44)
де
![]() ,
,
![]() ,
,
![]() – сталі, які визначаються із умов
закріплення.
– сталі, які визначаються із умов
закріплення.
Перший
доданок у другому співвідношенні (8.44)
при обході замкненого контуру, тобто
при зміні
![]() від 0 до
від 0 до
![]() ,
одержить приріст
,
одержить приріст
![]() .
Це означає, що у випадку неоднозв’язної
області (кругове кільце) зміщення
.
Це означає, що у випадку неоднозв’язної
області (кругове кільце) зміщення
![]() будуть однозначними тільки при
будуть однозначними тільки при
![]() .
Тому для кругового кільця у формулах
(8.35)-(8.38) необхідно покласти
.
Тому для кругового кільця у формулах
(8.35)-(8.38) необхідно покласти
![]() .
.
Розглянемо розв’язки деяких типових задач.
-
Порожнистий циліндр під дією рівномірного зовнішнього і внутрішнього тисків (задача Ламе). Нехай порожнистий круговий циліндр із зовнішнім радіусом
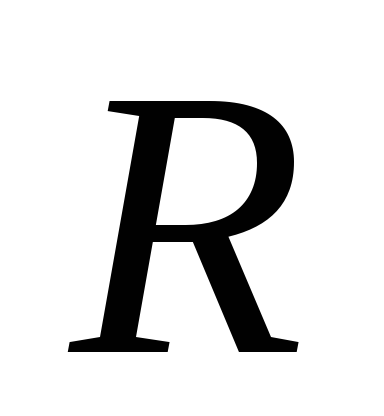 і внутрішнім
і внутрішнім
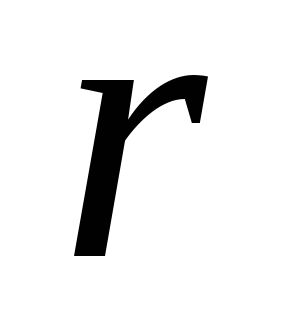 перебуває під дією рівномірного
зовнішнього
перебуває під дією рівномірного
зовнішнього
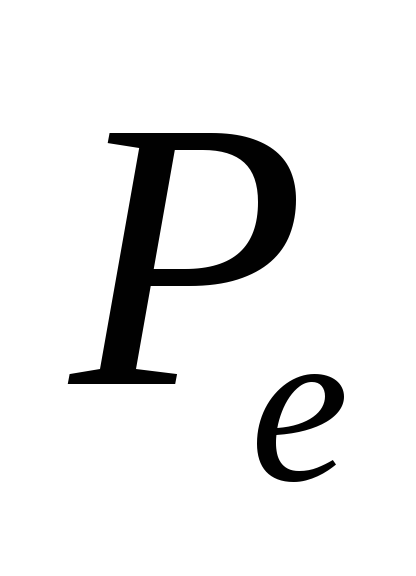 та внутрішнього
та внутрішнього
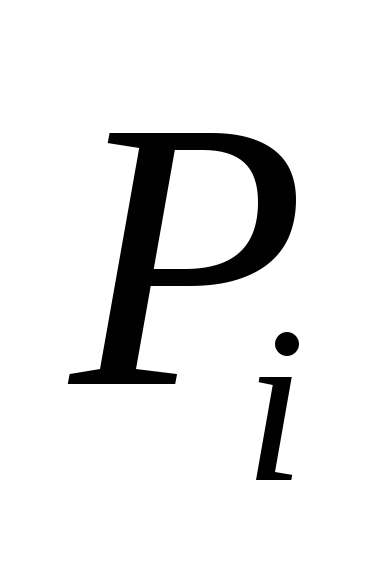 тисків (рис. 8.7).
тисків (рис. 8.7).

Рис. 8.7
Компоненти
тензора напружень у двозв’язній області
визначаються за формулами (8.36) при
![]()
![]() ;
;
![]() ;
;
![]() . (8.45)
. (8.45)
Граничні умови задачі мають вигляд
![]() ;
;
![]() ;
;
![]() ;
;
![]() (8.46)
(8.46)
і
дозволяють визначити сталі
![]() ,
,
![]() ,
,
![]() із системи рівнянь
із системи рівнянь
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (8.47)
. (8.47)
Враховуючи значення цих сталих
![]() ;
;
![]() ;
;
![]() ,
,
із формул (8.45) визначаємо
![]()
![]() ;
;
![]()
![]() ;
;
![]() . (8.48)
. (8.48)
Оскільки
компоненти вектора зміщення не залежить
від
![]() ,
то за формулами (8.44) знаходимо
,
то за формулами (8.44) знаходимо
 ;
;
![]() . (8.49)
. (8.49)
Зміщення
![]() виражає собою поворот циліндра навколо
його осі, як абсолютно твердого тіла.
виражає собою поворот циліндра навколо
його осі, як абсолютно твердого тіла.
-
Чистий згин кривого стержня вузького прямокутного перерізу (задача Х.С. Головіна). Розглянемо стержень сталого поперечного перерізу з круговою віссю радіусом
 ,
де
,
де
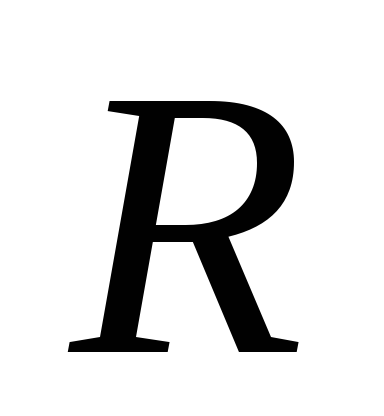 і
і
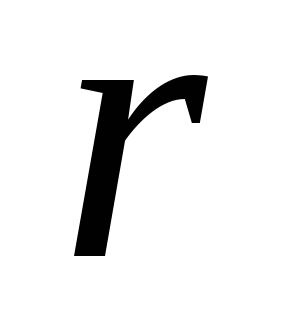 – зовнішній і внутрішній радіуси,
згинається в площині кривини моментами
– зовнішній і внутрішній радіуси,
згинається в площині кривини моментами
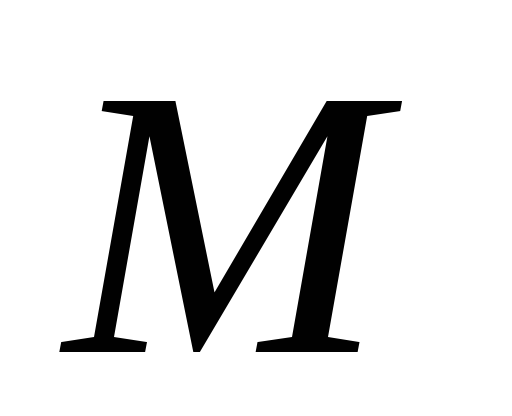 ,
прикладеними до його торців (рис. 8.8).
,
прикладеними до його торців (рис. 8.8).
Рис.
8.8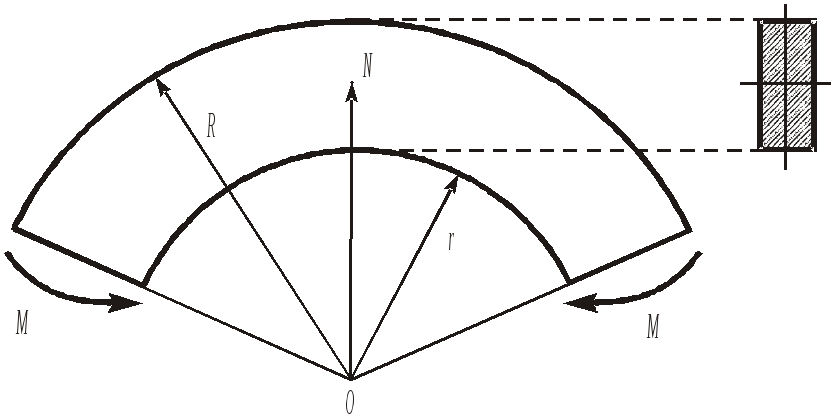 Н
Н
![]() ,
тому функцію напружень вибираємо у
вигляді (8.35). Відповідні цій функції
напруження визначаються за формулами
(8.36).
,
тому функцію напружень вибираємо у
вигляді (8.35). Відповідні цій функції
напруження визначаються за формулами
(8.36).
Граничні умови задачі на криволійнійних контурах стержня мають вигляд:
![]() ;
;
![]() (8.50)
(8.50)
і на його торцях
![]() ;
;
![]() . (8.51)
. (8.51)
Першу умову (8.51) перетворимо так
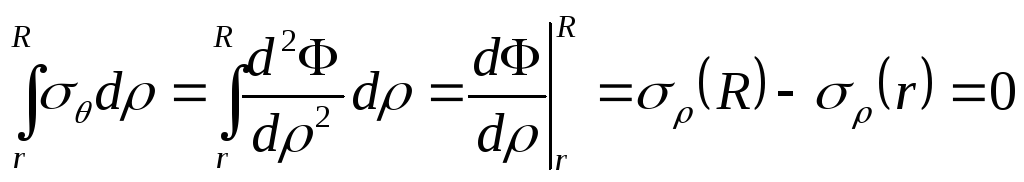 . (8.52)
. (8.52)
Внаслідок (8.50) остання умова виконується тотожно. Із другої умови (8.51) знаходимо з урахуванням (8.27)
![]()
![]() . (8.53)
. (8.53)
Підставляючи
(8.36) в граничні умови (8.50), враховуючи
при цьому (8.53), одержимо систему рівнянь
для визначення сталих
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (8.54)
. (8.54)
Якщо розв’язок системи (8.54) стане відомим, то за формулами (8.36) визначаємо компоненти тензора напружень
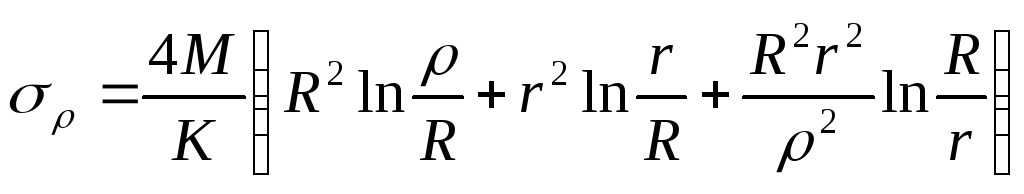 ;
;
![]() ;
;
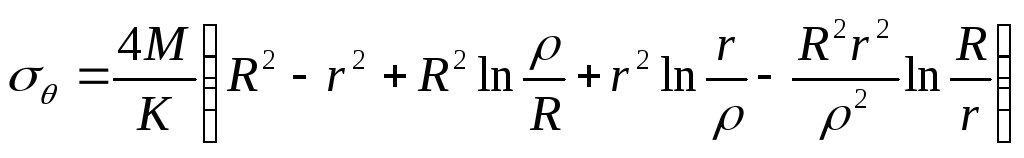 , (8.55)
, (8.55)
де
![]() ,
а компоненти вектора зміщення – із
співвідношень (8.44), в яких сталі
,
а компоненти вектора зміщення – із
співвідношень (8.44), в яких сталі
![]() ,
,
![]() ,
,
![]() знаходимо із умов закріплення стержня.
знаходимо із умов закріплення стержня.
