
- •Декартовий добуток множин.
- •VIII. Зображення декартового добутку множин на координатній площині
- •2 Семестр
- •Про історію виникнення натурального числа.
- •Порядкові і кількісні натуральні числа. Рахунок.
- •Теоретико – множний зміст кількісного числа і нуля.
- •Додавання. Закони додавання.
- •1. Порівняння.
- •Правила віднімання числа з суми і суми із числа:
- •Поняття відношення подільності.
- •Властивості відношення подільності.
- •Подільність суми, різниці і добутку цілих невід‘ємних чисел.
- •Признаки подільності чисел.
- •Найбільший спільний дільник і найменше спільне кратне.
- •Властивості нсд.
- •Властивості нск.
- •Признаки подільності на складові числа.
- •Знаходження нсд і нск чисел способом розкладу на прості множники.
- •Алгоритм Евкліда.
- •II курс
- •I. Поняття функції.
- •Способи завдання функції.
- •Властивості функції.
- •Графік функції.
- •Лінійні функції, їх властивості і графік.
- •Обернена залежність, її властивості.
- •Квадратичні функції, їх властивості.
- •Довжина відрізку і її вимірювання.
- •Площа фігури, способи її вимірювання.
- •Об‘єм тіла, його вимірювання.
- •Маса, вартість, швидкість, час. Одиниці вимірювання.
- •VI. Залежність між величинами.
- •Числовий вираз і його значення.
- •Вираз зі змінною і його область визначення.
- •Тотожні перетворення виразів.
- •Означення рівняння.
- •Рівносильні рівняння.
- •Властивості рівнянь.
- •Числові Нерівності.
- •2. Основні властивості нерівностей.
- •4 Семестр
- •Геометричні фігури.
- •Кути, їх види, побудова.
- •Признак паралельності прямих.
- •Перпендикуляр до прямої.
Лекція 1. Математичні поняття.
Мета:
Основні питання:
-
Вступ.
-
Об‘єм і зміст поняття.
-
Означення понять.
-
Вимоги до означення понять.
-
Вступ. Математика, як і інші науки, вивчає навколишнє середовище, природні та суспільні явища, але вивчає лише їх з особливого боку. Наприклад, в геометрії вивчають форму і розміри предметів, не враховуючи інші властивості: колір, масу і т.д. тому в геометрії замість слова «предмет» кажуть: «геометрична фігура». Відрізок, промінь, пряма, кут, коло, квадрат – геометричні фігури. Результатом абстрагування являються також найважливіші математичні поняття, як «число» і «величина». Взагалі будь-які математичні об‘єкти – це результат відокремлення з предметів і явищ навколишнього середовища кількісних і просторових властивостей і відношень і абстрагування їх від всіх інших властивостей. Як сказав Ф. Енгельс: «математика – це наука про кількісні форми і просторові уявлення реального світу». Математичні об‘єкти реально не існують, не існує в навколишньому світі геометричних фігур, чисел. Всі вони утворені людьми в процесі історичного розвитку суспільства і існує лише в розумінні людини і в тих знаках і символах, які утворюють математичну мову.
-
Об‘єм і зміст поняття. Будь – який математичний об‘єкт має певні властивості. Наприклад, квадрат має чотири сторони, чотири прямих кута, рівні діагоналі. Можна вказати і інші властивості квадрата. Серед властивостей об‘єкта розрізнюють властивості суттєві і несуттєві для його виділення з інших об‘єктів. Властивість вважають суттєвою для об‘єкта, якщо вона притаманна цьому об‘єкту і без нього він не може існувати. Несуттєвими властивостями вважають такі, відсутність яких не впливає на існування об‘єкта. Щоб розуміти, що представляє собою даний об‘єкт достатньо знати його суттєві властивості. В цьому випадку кажуть, що мають поняття про цей об‘єкт. Сукупність всіх взаємозв’язаних суттєвих властивостей об‘єкта називають змістом поняття про цей об‘єкт. Об‘єм поняття – це сукупність всіх об‘єктів, які позначені одним терміном. Таким чином, всяке поняття характеризується терміном, об‘ємом і змістом. Між об‘ємом поняття і його змістом існує зв‘язок: чим «більше» об‘єм поняття, тим «менше»його зміст, і навпаки. Наприклад, об‘єм поняття «прямокутний трикутник» «менше» об’єму поняття «трикутник», оскільки в об‘єм першого поняття входять не всі трикутники, а тільки прямокутні. Але зміст першого поняття «більше» змісту другого: прямокутний трикутник має не лише всі властивості трикутника, але і іншими, які притаманні тільки прямокутним трикутникам.
-
Означення понять. Зміст поняття о будь-яком математичному об‘єкті містить багато різних суттєвих властивостей цього об‘єкта. Але щоб встановити, чи міститься об‘єкт в об‘ємі даного поняття (тобто разпознати його), необхідно перевірити наявність у нього лише деяких суттєвих властивостей. Встановлення цих суттєвих властивостей об‘єкта, яких достатньо для распознавння об‘єкта, називається означенням поняття про цей об‘єкт. Взагалі, означення – це логічна операція, яка розкриває зміст поняття. Способи означення поняття є різні. Перед усім розрізняють явні і неявні означення. Явні поняття мають форму рівності, спів падіння двох понять, або ототожнюються два поняття. Одне з них називають визначним поняттям, друге – визначальним. Через визначальне розкривається зміст визначного поняття. Проаналізуємо, наприклад, структуру означення квадрата: «Квадратом називається прямокутник, у якого всі сторони рівні». Вона є такою: спочатку вказане визначне поняття – «квадрат», а потім приведене визначальне, яке включає властивості: бути прямокутником, мати всі рівні сторони. Властивість «бути прямокутником» показує, що всі квадрати являються прямокутниками, тобто поняття прямокутник являється більш загальним, ніж поняття квадрат. Його називають родовим по відношенню до визначного поняття «квадрат». Друга властивість – «мати рівні сторони» - це виділення видової властивості, яка відокремлює квадрат від інших видів прямокутника. Схематично структуру таких означень можна представити наступним чином: МАЛЮНОК. Неявні означення не мають форми спів падіння двох понять. Прикладами таких означень являються так звані контекстуальні і остенсивні означення. В контекстуальних означеннях зміст нового поняття розкривається через уривок тексту, через контекст, через аналіз конкретної ситуації, яка описує зміст нового поняття. Прикладом такого означення може бути означення рівняння і його розв‘язок. Остенсивні означення використовують для введення термінів шляхом демонстрації об‘єктів, які цими термінами позначають. Тому остенсивні означення називають ще означеннями шляхом показу. Зустрічаються в математиці і означення, побудовані по іншому. Наприклад, означення трикутника: «Трикутником називається фігура, яка складається з трьох точок. Які не лежать на одній прямій, і трьох відрізків, які попарно з‘єднують ці точки». В цьому означенні вказане родове поняття по відношенню до трикутника – фігура, а потім вказаний спосіб побудови такої фігури, такі означення називають генетичними. Розглянемо означення арифметичної прогресії: «Арифметичною прогресією називається числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому, доданого з одним числом». Тут визначне поняття – «арифметична прогресія», родове поняття – «числова послідовність», а далі описується спосіб отримання всіх членів прогресії по заданій формулі. Таке означення називають індуктивним (рекурентним).
-
Вимоги до означень. Щоб оцінити правильність явних означень, необхідно знати правила означення понять.1) Перш за все визначне і визначальне поняття повинні бути еквівалентні (сорозмірні). Це означає, що сукупність предметів, які є охоплені ними, мають співпадати. Наприклад, правильним є означення: «прямокутник – це чотирикутник, у якого всі кути прямі». Неправильним означенням є таке:»Прямі
 називаються паралельними, якщо вони
не мають спільних точок або співпадають»
(занадто широко, тому що йому задовольняють
і мимобіжні прямі). Або невірним є:
«прямі
називаються паралельними, якщо вони
не мають спільних точок або співпадають»
(занадто широко, тому що йому задовольняють
і мимобіжні прямі). Або невірним є:
«прямі
 називаються паралельними, якщо вони
не мають спільних точок» (занадто
вузько, тому що йому не задовольняють
прямі, які співпадають). 2) Друге правило
означення забороняє
порочний круг: не можна
визначати поняття через само себе або
визначати його через інше поняття,
яке, в свою чергу, визначається через
нього. Наприклад, множенням називається
дія, за допомогою якої знаходять добуток
цих чисел – неправильне означення. 3)
В означенні мають бути
вказані всі властивості, які дозволяють
однозначно виділити об‘єкти, що
належать об‘єму визначального поняття.
Наприклад, «Суміжними кутами називаються
кути, які в сумі складають
називаються паралельними, якщо вони
не мають спільних точок» (занадто
вузько, тому що йому не задовольняють
прямі, які співпадають). 2) Друге правило
означення забороняє
порочний круг: не можна
визначати поняття через само себе або
визначати його через інше поняття,
яке, в свою чергу, визначається через
нього. Наприклад, множенням називається
дія, за допомогою якої знаходять добуток
цих чисел – неправильне означення. 3)
В означенні мають бути
вказані всі властивості, які дозволяють
однозначно виділити об‘єкти, що
належать об‘єму визначального поняття.
Наприклад, «Суміжними кутами називаються
кути, які в сумі складають
 »
(недостатньо властивостей). 4) Ще одне
правило до означення – відсутність
в ньому збитку. Це
позначає, що в означенні не повинно
бути вказано зайвих властивостей, які
випливають з інших властивостей, також
включених в означення поняття. Наприклад,
«прямокутником називається чотирикутник,
у якого всі сторони рівні і всі кути
прямі».це означення має зайву властивість,
краще сказати так: «Прямокутником
називається чотирикутник, у якого всі
кути прямі». Треба сказати, що в
будь-якому означенні є елемент
довільності, що проявляється, по-перше,
в виборі терміна, а по-друге, в виборі
властивостей, які включаються в
означення. Якщо одному поняття дається
два різних означення, то вони повинні
бути рівносильними. Це позначає, що з
властивостей, що включені в одне
означення, мають випливати властивості,
покладені в основу другого означення,
і навпаки. При виборі означення
користуються тим, яке означення
простіше, натуральніше або корисніше
для подальшої побудови теорії.
»
(недостатньо властивостей). 4) Ще одне
правило до означення – відсутність
в ньому збитку. Це
позначає, що в означенні не повинно
бути вказано зайвих властивостей, які
випливають з інших властивостей, також
включених в означення поняття. Наприклад,
«прямокутником називається чотирикутник,
у якого всі сторони рівні і всі кути
прямі».це означення має зайву властивість,
краще сказати так: «Прямокутником
називається чотирикутник, у якого всі
кути прямі». Треба сказати, що в
будь-якому означенні є елемент
довільності, що проявляється, по-перше,
в виборі терміна, а по-друге, в виборі
властивостей, які включаються в
означення. Якщо одному поняття дається
два різних означення, то вони повинні
бути рівносильними. Це позначає, що з
властивостей, що включені в одне
означення, мають випливати властивості,
покладені в основу другого означення,
і навпаки. При виборі означення
користуються тим, яке означення
простіше, натуральніше або корисніше
для подальшої побудови теорії.
-
Лекція 2. Математичні твердження.
Мета:
Основні питання:
-
Елементарні і складові твердження.
-
Висловлення.
-
Висловлювані форми.
-
Квантори.
-
Правила побудови заперечень висловів, які містять квантори.
-
Елементарні і складові твердження. В пізнанні оточуючого світу, людина встановлює різноманітні зв‘язки між об‘єктами, між об‘єктами і їх властивостями та ін. кожне математичне речення характеризується змістом і логічною структурою. Розглянемо уважніше структуру тверджень. В математиці розрізнюють елементарні і складові твердження. Твердження «число 28 ділиться на 7» є елементарним. Складовими твердженнями являються, наприклад, наступні: «число 28 парне і ділиться на 7», «число 5 менше або дорівнює 8», «якщо трикутник рівнобедрений, то кути в ньому при основі рівні», «число 14 не ділиться на 4». Складові твердження утворюються з елементарних за допомогою слів «і», «або», частки «не», «якщо, то». Ці слова в математиці називають логічними зв‘язками. Виявити логічну структуру складового твердження – значить встановити: 1) з яких елементарних тверджень утворено складове твердження, 2) за допомогою яких логічних зв‘язок воно утворене. (розглянути приклади, які наведені раніше).
-
Висловлення. Серед суджень, які встановлюють різноманітні відношення між математичними поняттями, вислови і висловлювані форми. Висловом називається твердження, відносно якого має сенс питання, істинно воно чи хибне. Наприклад, «число 6 парне» є істинним висловом, а «2+4=9» - хибним. Кожному вислову приписують одне з двох значень: І(істина), якщо воно істинне, і Х(хибність), якщо воно хибне. Значення І і Х називають значеннями істинності висловлення. Якщо висловлення елементарне, то його значення істинності визначають по змісту, спираючись на відомі факти. В складових висловленнях на допомогу приходить форма висловлення. Вважають, що вислів виду «А і В» істинний, якщо істинні обидва вислови А і В. якщо хоча б одне з них є хибним, то вислів «А і В» є хибним. Висловлення виду «А або В» вважають істинним, якщо істинний хоча б один з висловів А і В. Висловлення «А або В» хибне, коли хибні обидва вислови А і В. Часто в математиці приходиться будувати висловлення, в яких щось заперечується. Заперечення вислову
 позначається
позначається
 і читають «не А»
або «невірно, що А». Взагалі запереченням
вислову А вважається істинним, коли
вислів А хибний, і «не А» є хибним, коли
А істинний. ТАБЛИЦЯ.
і читають «не А»
або «невірно, що А». Взагалі запереченням
вислову А вважається істинним, коли
вислів А хибний, і «не А» є хибним, коли
А істинний. ТАБЛИЦЯ. -
Висловлювані форми. В математиці часто зустрічаються твердження, які містять одну або декілька змінних. Наприклад,
 .
Ці твердження не являються висловами,
так як відносно їх не має сенсу питання,
істинні вони чи хибні. Але при підстановці
значень змінних ці твердження
перетворюються в вислови істинні або
хибні. Твердження такого виду називають
висловлюваними формами.
Кожна висловлювана форма породжує
вислів тієї ж форми. Наприклад,
.
Ці твердження не являються висловами,
так як відносно їх не має сенсу питання,
істинні вони чи хибні. Але при підстановці
значень змінних ці твердження
перетворюються в вислови істинні або
хибні. Твердження такого виду називають
висловлюваними формами.
Кожна висловлювана форма породжує
вислів тієї ж форми. Наприклад,
 дозволяє
отримати вислови
дозволяє
отримати вислови
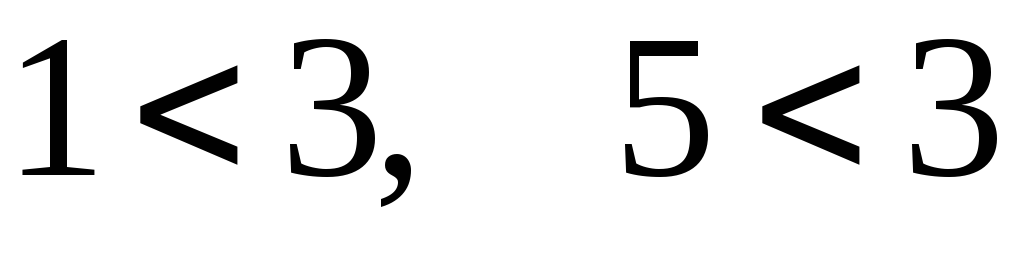 .
Висловлювана форма
– це твердження з однією або декількома
змінними, яке обертається в висловлення
при підстановці в нього конкретних
значень змінних. Також як і висловлення,
висловлювані форми бувають елементарними
і складовими. Складові утворюються з
елементарних за допомогою логічних
зв‘язок «і», «або», «не» і т.д.
.
Висловлювана форма
– це твердження з однією або декількома
змінними, яке обертається в висловлення
при підстановці в нього конкретних
значень змінних. Також як і висловлення,
висловлювані форми бувають елементарними
і складовими. Складові утворюються з
елементарних за допомогою логічних
зв‘язок «і», «або», «не» і т.д. -
Квантори. Про числа 0,1,2,3,4,5,6,7,8,9 можна сказати: всі подані числа однозначні і деякі з цих чисел є парними. Так як відносно цих тверджень можна сказати, що вони істинні чи хибні, то отримані твердження – висловлення. Слова «всі» і «деякі» називають кванторами. Слово квантор з латинського перекладається як «скільки», тобто квантор показує, о скількох (всіх або деяких) об‘єктах йдеться в твердженнях. Розрізняють квантори спільності і існування. Квантори спільності – це слова «будь-який», «всякий», «кожний», «всі». Квантори існування – це слова «існує», «деякі», «хоча б один». Таким чином, якщо перед висловлюваною формою поставити деякий квантор, то отримаємо вислів. Форму висловлення з квантором мають більшість математичних тверджень. Наприклад, всі квадрати являються прямокутниками; деякі парні числа діляться на 4; в будь-якому прямокутнику сума внутрішніх кутів дорівнює
 .
Істинність
висловів з кванторами спільності
встановлюється шляхом доведення.
Щоб впевнитися в хибності
таких висловів, достатньо навести контр
приклад. Наприклад, 1)
Будь-яке число 0,1,2,3,4,5,6,7,8,9 являється
розв‘язком нерівності
.
Істинність
висловів з кванторами спільності
встановлюється шляхом доведення.
Щоб впевнитися в хибності
таких висловів, достатньо навести контр
приклад. Наприклад, 1)
Будь-яке число 0,1,2,3,4,5,6,7,8,9 являється
розв‘язком нерівності
 (підставляючи
всі значення в нерівність довели
істинність вислову, а значить, за
індукцією, будь-яке дійсне число
задовольняє нерівності). 2) Сума будь-яких
послідовних натуральних чисел ділиться
на 3 (істинність доводиться безпосередньо).
3) будь-який прямокутник являється
квадратом (достатньо накреслити
прямокутник, який не являється квадратом
і доведена хибність вислову – контр
приклад). Істинність
висловів з кванторами
існування
встановлюється за допомогою конкретного
прикладу. Щоб впевнитися
в хибності
такого вислову, необхідно провести
доведення. Наприклад,
1) існують натуральні числа, кратні 3
(6, 9, 12 і т.д.). 2) Існують прямокутні
рівносторонні трикутники (є хибним,
тому що в прямокутному трикутнику один
кут обов‘язково прямий, а в рівносторонньому
всі кути містять
(підставляючи
всі значення в нерівність довели
істинність вислову, а значить, за
індукцією, будь-яке дійсне число
задовольняє нерівності). 2) Сума будь-яких
послідовних натуральних чисел ділиться
на 3 (істинність доводиться безпосередньо).
3) будь-який прямокутник являється
квадратом (достатньо накреслити
прямокутник, який не являється квадратом
і доведена хибність вислову – контр
приклад). Істинність
висловів з кванторами
існування
встановлюється за допомогою конкретного
прикладу. Щоб впевнитися
в хибності
такого вислову, необхідно провести
доведення. Наприклад,
1) існують натуральні числа, кратні 3
(6, 9, 12 і т.д.). 2) Існують прямокутні
рівносторонні трикутники (є хибним,
тому що в прямокутному трикутнику один
кут обов‘язково прямий, а в рівносторонньому
всі кути містять
 ,
значить, серед прямокутних трикутників
рівносторонніх не існує).
,
значить, серед прямокутних трикутників
рівносторонніх не існує). -
Правила побудови заперечень висловів, які містять квантори. Заперечення висловів з квантором (спільності або існування) може бути побудоване двома способами:
1) перед даним висловом ставляться слова «невірно що»; 2) квантор спільності (існування) замінюється квантором існування (спільності), а твердження, яке стояло після квантора, замінюється його запереченням. Сформульоване правило являється достатнім для правильної побудови заперечення висловів з квантором. Заперечення даного вислову може бути побудовано і в іншій формі. Важливо тільки не забути вимогу: якщо вислів хибний, то його заперечення повинно бути істинним, і навпаки. Наприклад, 1) «деякі непарні числа діляться на 4» - хибність, його заперечення: «невірно, що деякі числа діляться на 4», або «всі непарні числа не діляться на 4». 2) «всі натуральні числа діляться на 3» - хибність, його заперечення має вид: «невірно, що всі натуральні числа діляться на 3», або «існують натуральні числа, які не діляться на 3».
Лекція 3. Математичні доведення.
Мета:
Основні питання:
-
Відношення рівнозначності між твердженнями.
-
Необхідні і достатні умови.
-
Структура і види теорем.
-
Дедуктивні міркування.
-
Найпростіші схеми дедуктивних міркувань.
-
Неповна індукція.
-
Відношення рівнозначності між твердженнями. Будь-яке міркування не обходиться без слів «випливає», «значить». Кажуть, що з твердження А випливає твердження В, якщо всякий раз, коли істинний вислів А, істинним є вислів В. наприклад, твердження «із того, що число а кратно 4, випливає, що воно кратно 2» можна сформулювати ще і так: всяке число, яке ділиться на 4, ділиться на 2, або якщо число ділиться на 4, то воно ділиться і на 2, число а ділиться на 4, значить воно ділиться на 2. Якщо із твердження А випливає твердження В, а із твердження В випливає твердження А, то кажуть, твердження А і В рівнозначні. Згідно цього означення твердження «трикутник «рівнобедрений» і «кути при основі трикутника рівні» є рівнозначними.
-
Необхідні і достатні умови. Якщо з твердження А випливає твердження В, то говорять, що В – необхідна умова для А, а А – достатня для В. іншими словами, вислів В називається необхідною умовою для А, якщо воно логічно випливає з А. вислів А називається достатньою умовою для В, якщо В з нього випливає. Якщо твердження А і В рівнозначні, то говорять, А – необхідна і достатня умова для В, і навпаки. Наприклад, в геометрії доведено, що з твердження «кути вертикальні» випливає твердження «кути рівні». тому згідно даному означенню можна сказати, що рівність кутів – необхідна умова для того, щоб кути були вертикальні, а вертикальність кутів є достатньою умовою для їх рівності. У зв‘язку з цим твердження «якщо кути вертикальні, то вони рівні» можна сформулювати інакше: для того, щоб кути були вертикальні, необхідно, щоб вони були рівні; для того, щоб кути були рівні, достатньо, щоб вони були вертикальні.
В – необхідна умова для А
А – достатня умова для В
-
Структура і види теорем. Раніше було відокремлено, що суттєві властивості об‘єкта утворюють зміст поняття про цей об‘єкт. Частина цих властивостей включається в означення поняття. Щоб мати більш повне уявлення про об‘єкт, вивчають і інші його властивості. Властивості основних (первісних) понять розкривається в аксіомах – твердженнях, які приймаються без доведення. Наприклад, властивості основних понять геометрії: точка, пряма, площини включені в аксіоми. Взагалі система аксіом будь-якої теорії, розкриваючи властивості основних понять, дає, по суті, їх означення, які називаються аксіоматичними. Властивості, які доводяться, найчастіше називають теоремами, іноді слідствами, признаками. В алгебрі – формулами, тотожностями, правилами. Тому, теорема – це висловлення про те, що з властивості А випливає властивість В. істинність цього вислову встановлюється шляхом доведення. В якому б виді не була сформульована теорема, в ній завжди виділяється умова А(що задано) і висновок В (що треба довести). Теореми
 і
і називаються оберненими
одна до іншої, а теореми
називаються оберненими
одна до іншої, а теореми
 і
і
 називаються протилежними. Наприклад,
для теореми «якщо кути вертикальні, то
вони рівні» оберненою є «якщо кути
рівні, то вони вертикальні», що являється
хибність. Протилежною до заданої є
«якщо кути не являються вертикальними,
то вони не рівні» також є хибність. А
ось обернена до протилежної «якщо кути
не рівні, то вони не вертикальні»
являється істиною. Встановлено, теореми
називаються протилежними. Наприклад,
для теореми «якщо кути вертикальні, то
вони рівні» оберненою є «якщо кути
рівні, то вони вертикальні», що являється
хибність. Протилежною до заданої є
«якщо кути не являються вертикальними,
то вони не рівні» також є хибність. А
ось обернена до протилежної «якщо кути
не рівні, то вони не вертикальні»
являється істиною. Встановлено, теореми
 і
і
 рівнозначні. Це називається законом
контра позиції. Якщо задана теорема і
і їй обернена являються вірними, то їх
можна об‘єднати в одну за допомогою
слів «тоді і тільки тоді» або «необхідно
і достатньо».
рівнозначні. Це називається законом
контра позиції. Якщо задана теорема і
і їй обернена являються вірними, то їх
можна об‘єднати в одну за допомогою
слів «тоді і тільки тоді» або «необхідно
і достатньо». -
Дедуктивні міркування. Довести теорему
 - значить встановити логічним шляхом,
що завжди, коли виконується властивість
А, буде виконуватись і властивість В.
доведення в математиці обладає рядом
особливостей. Часто воно проводиться
за правилами логіки без яких-то посилань
на наглядність і дослід. В основі
доведення лежить міркування
– логічна операція, в результаті якої
із одного чи декількох взаємозв‘язаних
по змісту тверджень отримаємо твердження,
яке містить нові (по відношенню до
заданих) знання. В якості приклада
розглянемо міркування першокласника,
якому необхідно встановити відношення
«менше» між числами 7 і 8. учень говорить:
«
- значить встановити логічним шляхом,
що завжди, коли виконується властивість
А, буде виконуватись і властивість В.
доведення в математиці обладає рядом
особливостей. Часто воно проводиться
за правилами логіки без яких-то посилань
на наглядність і дослід. В основі
доведення лежить міркування
– логічна операція, в результаті якої
із одного чи декількох взаємозв‘язаних
по змісту тверджень отримаємо твердження,
яке містить нові (по відношенню до
заданих) знання. В якості приклада
розглянемо міркування першокласника,
якому необхідно встановити відношення
«менше» між числами 7 і 8. учень говорить:
« ,
тому що 7 при рахунку називають раніше,
ніж 8». На які ж факти він опирався,
стверджуючи це. По-перше, якщо число а
при рахунку називають раніше числа в,
то
,
тому що 7 при рахунку називають раніше,
ніж 8». На які ж факти він опирався,
стверджуючи це. По-перше, якщо число а
при рахунку називають раніше числа в,
то
 для будь-яких натуральних чисел. І
по-друге, 7 при рахунку називають раніше,
ніж 8. перше твердження носить загальний
характер, так як містить квантор
спільності, його називають загальною
посилкою. Друге
твердження стосується конкретних чисел
7 і 8, відображає частинний випадок, його
називають частковою
посилкою. З двох посилок
і випливає новий факт
для будь-яких натуральних чисел. І
по-друге, 7 при рахунку називають раніше,
ніж 8. перше твердження носить загальний
характер, так як містить квантор
спільності, його називають загальною
посилкою. Друге
твердження стосується конкретних чисел
7 і 8, відображає частинний випадок, його
називають частковою
посилкою. З двох посилок
і випливає новий факт
 ,
його називають висновком.
Міркування, між посилками і висновком
якого має місце відношення слідування,
називають дедуктивним.
Іншими словами, міркування є дедуктивним,
якщо за допомогою його з істинних
посилок не можна отримати хибний
висновок. Інакше міркування не являється
дедуктивним.
,
його називають висновком.
Міркування, між посилками і висновком
якого має місце відношення слідування,
називають дедуктивним.
Іншими словами, міркування є дедуктивним,
якщо за допомогою його з істинних
посилок не можна отримати хибний
висновок. Інакше міркування не являється
дедуктивним. -
Найпростіші схеми дедуктивних міркувань. Вважають, що в основі кожного дедуктивного міркування лежить певне правило висновку. 1) Правило висновку (
 і
і
 ,
де
,
де
 - загальна посилка,
- загальна посилка,
 - часткова посилка і
- часткова посилка і
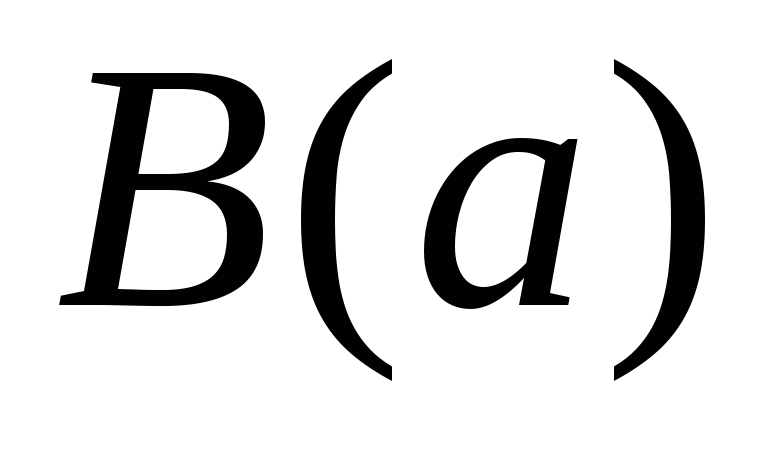 - висновок. 2) Правило
заперечення
- висновок. 2) Правило
заперечення
 .
3) Правило силогізму
.
3) Правило силогізму
 .
Застосування цих правил гарантує, що
міркування буде дедуктивним, тобто
дозволяє з істинних посилок виводити
істинні висновки. Наприклад, 1) Всі
числа, запис яких закінчується нулем,
діляться на 5; число не ділиться на 5,
значить, його запис не закінчується 0.
2) Якщо натуральне число кратне 8, то
воно кратне 4; якщо натуральне число
кратне 4, то воно кратне 2; значить, якщо
число кратне 8, то воно кратне 2. 3) Якщо
запис числа закінчується нулем, то воно
ділиться на 5; число не закінчується
нулем, значить, воно не ділиться на 5.
.
Застосування цих правил гарантує, що
міркування буде дедуктивним, тобто
дозволяє з істинних посилок виводити
істинні висновки. Наприклад, 1) Всі
числа, запис яких закінчується нулем,
діляться на 5; число не ділиться на 5,
значить, його запис не закінчується 0.
2) Якщо натуральне число кратне 8, то
воно кратне 4; якщо натуральне число
кратне 4, то воно кратне 2; значить, якщо
число кратне 8, то воно кратне 2. 3) Якщо
запис числа закінчується нулем, то воно
ділиться на 5; число не закінчується
нулем, значить, воно не ділиться на 5. -
Неповна індукція. Відомо, що 15 ділиться на 5, 25 ділиться на 5, 35 і 95 діляться на 5. враховуючи це, робимо висновок, що будь-яке число, запис якого закінчується цифрою 5, ділиться на 5. В розглянутому міркуванні на основі ряду часткових випадків робимо висновок загальний. Такі міркування називають неповною індукцією. Неповна індукція представляє собою таке міркування, при якому на основі того, що деякі об‘єкти сукупності мають певні властивості, робиться висновок про те, що ці властивості притаманні всім об‘єктам цієї сукупності. Висновки, отримані при неповній індукції, можуть бути як істинними, так і хибними. Так висновок про те, що кожне число, запис якого закінчується цифрою 5, ділиться на 5, істинний. А твердження «при будь-якому натуральному числі
 значення
виразу
значення
виразу
 є просте число» хибне. Дійсно, якщо
є просте число» хибне. Дійсно, якщо
 ,
то отримаємо значення
,
то отримаємо значення
 ,
тобто даний вираз є складовим числом.
До висновків, отриманих за допомогою
неповної індукції, треба відноситись
критично. Ці висновки носять характер
гіпотези, догадки, яку слідує або довести
(дедуктивним методом), або спростити.
Таким чином, в процесі пізнань дедуктивні
і індуктивні міркування виявляються
взаємозв‘язаними. При тому що індуктивні
міркування не завжди приводять до
правильних висновків, роль їх в вивченні
математики і інших науках дуже велика.
В ході індуктивних міркувань формується
вміння бачити загальне в конкретних,
часткових випадках, висловлювати
догадки.
,
тобто даний вираз є складовим числом.
До висновків, отриманих за допомогою
неповної індукції, треба відноситись
критично. Ці висновки носять характер
гіпотези, догадки, яку слідує або довести
(дедуктивним методом), або спростити.
Таким чином, в процесі пізнань дедуктивні
і індуктивні міркування виявляються
взаємозв‘язаними. При тому що індуктивні
міркування не завжди приводять до
правильних висновків, роль їх в вивченні
математики і інших науках дуже велика.
В ході індуктивних міркувань формується
вміння бачити загальне в конкретних,
часткових випадках, висловлювати
догадки.
Лекція5. Поняття множини.
Мета:
Основні питання:
-
Поняття множини і елемента множини.
-
Способи завдання множин.
-
Відношення між множинами.
-
Множина і поняття.
-
Поняття множини і елемента множини. В математиці часто приходиться розглядати певні групи об‘єктів як єдине ціле: числа від 1 до 10, натуральні числа, трикутники. Всі ці різноманітні сукупності називають множинами. Поняття множини являється одним з основних понять математики і тому не має означення через інші поняття. Його можна пояснити на прикладах: множина учнів класу, множина букв алфавіту, натуральні числа. В математиці розглядають множину, яка містить один об‘єкт, або не містить жодного елемента, яка називається пустою. Об‘єкти, з яких складається множина, називають його елементами. Часто приходиться з‘ясовувати належність елемента до розглянутої множини. Множини бувають скінчені і нескінчені. Скінченою множиною називають таку, елементи якої можна перерахувати. Нескінченими являються і множини чисел.
-
II.
Способи завдання множин.
Вважають, що множина визначається своїми
елементами, тобто множина задана,
якщо про будь-який об‘єкт можна сказати,
належить він цій множині чи не належить.
Множину можна задати, перерахувавши
всі його елементи.
Наприклад,
![]() .
Якщо множина нескінчена, то її елементи
перерахувати не можна. В таких випадках
вказують характеристичну
властивість його елементів.
Характеристична
властивість – це така
властивість, якою володіє кожний елемент,
який належить множині, і не володіє
жоден з елементів, який йому не належить.
Для того щоб задати деяку множину,
достатньо або перерахувати всі його
елементи, або вказати характеристичну
властивість його елементів. Наприклад,
множина А натуральних чисел, менших 7,
задана вказанням характеристичної
властивості його елементів, можна задати
і так:
.
Якщо множина нескінчена, то її елементи
перерахувати не можна. В таких випадках
вказують характеристичну
властивість його елементів.
Характеристична
властивість – це така
властивість, якою володіє кожний елемент,
який належить множині, і не володіє
жоден з елементів, який йому не належить.
Для того щоб задати деяку множину,
достатньо або перерахувати всі його
елементи, або вказати характеристичну
властивість його елементів. Наприклад,
множина А натуральних чисел, менших 7,
задана вказанням характеристичної
властивості його елементів, можна задати
і так:
![]() ,
тобто перерахував його елементи.
,
тобто перерахував його елементи.
III.
Відношення між множинами.
Задані дві множини:
![]() і
і
![]() .
Видно, що елементи
.
Видно, що елементи
![]() належать одночасно множині А і В. кажуть,
що ці елементи – спільні
для множин А і В, а самі множини
перетинаються.
Якщо множини не мають спільних елементів,
то говорять, що вони не
перетинаються. Множини
належать одночасно множині А і В. кажуть,
що ці елементи – спільні
для множин А і В, а самі множини
перетинаються.
Якщо множини не мають спільних елементів,
то говорять, що вони не
перетинаються. Множини
![]() і
і
![]() перетинаються, причому, кожний елемент
множини В являється елементом множини
А. в цьому випадку говорять, що множина
В включена в А або що множина В являється
підмножиною множини А. Множина В
називається підмножиною
множини А, якщо кожний
елемент множини В належить множині А,
і записують
перетинаються, причому, кожний елемент
множини В являється елементом множини
А. в цьому випадку говорять, що множина
В включена в А або що множина В являється
підмножиною множини А. Множина В
називається підмножиною
множини А, якщо кожний
елемент множини В належить множині А,
і записують
![]() .
Серед всіх підмножин заданої множини
повинні бути обов‘язково пуста множина
і сама множина. Якщо множини перетинаються,
причому кожний елемент множини А
являється елементом множини В, і навпаки,
кожний елемент множини В являється
елементом множини А, то говорять, що
множини А і В є рівними.
Тобто множини А і В називаються рівними,
якщо
.
Серед всіх підмножин заданої множини
повинні бути обов‘язково пуста множина
і сама множина. Якщо множини перетинаються,
причому кожний елемент множини А
являється елементом множини В, і навпаки,
кожний елемент множини В являється
елементом множини А, то говорять, що
множини А і В є рівними.
Тобто множини А і В називаються рівними,
якщо
![]() ,
,
![]() ,
записують
,
записують
![]() .
З означення випливає, що рівні множини
складаються з однакових елементів і що
порядок запису елементів множини не
являється суттєвим. Наглядно відношення
між множинами зображають за допомогою
особливих малюнків, які називають
кругами Ейлера.
Поняття множини і підмножини в початковій
математиці в явній формі не вивчається,
але задач, пов‘язаних з виділенням
деякої сукупності, учні розв‘язують
багато. Наприклад, «серед даних
чотирикутників вказати прямокутники»,
«назвати серед даних чисел парні».
.
З означення випливає, що рівні множини
складаються з однакових елементів і що
порядок запису елементів множини не
являється суттєвим. Наглядно відношення
між множинами зображають за допомогою
особливих малюнків, які називають
кругами Ейлера.
Поняття множини і підмножини в початковій
математиці в явній формі не вивчається,
але задач, пов‘язаних з виділенням
деякої сукупності, учні розв‘язують
багато. Наприклад, «серед даних
чотирикутників вказати прямокутники»,
«назвати серед даних чисел парні».
-
Множина і поняття. Як відомо, будь-яке поняття має об‘єм. З теоретик-множної позиції об‘єм поняття – це множина об‘єктів, які можна назвати одним словом, яке позначає поняття. Наприклад, об‘єм поняття «трикутник» - множина трикутників, об‘єм поняття «прямий кут» - множина прямих кутів. Підхід до об‘єму поняття як множині дає можливість наглядно уявити відношення між поняттями. Існують поняття, які не знаходяться в відношенні роду і виду. Наприклад, поняття «квадрат» і «трикутник» - їх об‘єми не знаходяться в відношенні включення.
Лекція 6, 7. Дії над множинами.
Мета:
Основні питання:
-
Перетин множин.
-
Об‘єднання множин.
-
Закони перетину і об‘єднання множин.
-
Доповнення підмножини.
-
Поняття розбиття множин на класи.
-
Задачі, пов‘язані з операціями над скінченими множинами.
-
Декартовий добуток множин.
-
Зображення декартового добутку множин на координатній площині.
I. Перетин
множин. З елементів
двох і більше множин можна утворити
нові множини. Вважають, що ці нові множини
являються результатом операцій над
множинами. Нехай задані дві множини:
![]() і
і
![]() .
Утворимо множину С, в яку включимо
спільні елементи множин А і В:
.
Утворимо множину С, в яку включимо
спільні елементи множин А і В:
![]() .
Отриману множину С називають перетином
множин А і В. Перетином
множин А і В називається
множина, яка містить тільки ті елементи,
які належать множині А і множині В.
Позначають
.
Отриману множину С називають перетином
множин А і В. Перетином
множин А і В називається
множина, яка містить тільки ті елементи,
які належать множині А і множині В.
Позначають
![]() і зображають МАЛ. В тому випадку, коли
множини А і В не мають спільних елементів,
говорять, що їх перетином являється
пуста множина. Операція, за допомогою
якої знаходять перетин множин, називається
перетином. Згідно означенню перетину
і зображають МАЛ. В тому випадку, коли
множини А і В не мають спільних елементів,
говорять, що їх перетином являється
пуста множина. Операція, за допомогою
якої знаходять перетин множин, називається
перетином. Згідно означенню перетину
![]() .
Якщо елементи множин А і В перелічені,
то щоб знайти їх перетин, достатньо
перелічити їх спільні елементи. Якщо
множини задані за допомогою характеристичною
властивістю, то з означення перетину
випливає, що ця характеристична
властивість перетину складається з
характеристичних властивостей заданих
множин за допомогою союзу «і».
.
Якщо елементи множин А і В перелічені,
то щоб знайти їх перетин, достатньо
перелічити їх спільні елементи. Якщо
множини задані за допомогою характеристичною
властивістю, то з означення перетину
випливає, що ця характеристична
властивість перетину складається з
характеристичних властивостей заданих
множин за допомогою союзу «і».
II.
Об‘єднання множин.
Об‘єднанням множин
А і В називається множина, яка містить
тільки такі елементи, які належать
множині А або множині В. позначають
![]() і зображають МАЛ. Операція, за допомогою
якої знаходять об‘єднання множин,
називається об‘єднанням. Згідно
означенню об‘єднання
і зображають МАЛ. Операція, за допомогою
якої знаходять об‘єднання множин,
називається об‘єднанням. Згідно
означенню об‘єднання
![]() .
Якщо елементи множин А і В перелічені,
то для того, щоб знайти їх об‘єднання,
достатньо перелічити елементи, які
належать хоча б одній множині. Наприклад,
.
Якщо елементи множин А і В перелічені,
то для того, щоб знайти їх об‘єднання,
достатньо перелічити елементи, які
належать хоча б одній множині. Наприклад,
![]() .
Якщо ж множини задані за допомогою
характеристичної властивості їх
елементів, то із означення об‘єднання
випливає, що характеристична властивість
об‘єднання складається з характеристичних
властивостей множин А і В за допомогою
союзу «або».
.
Якщо ж множини задані за допомогою
характеристичної властивості їх
елементів, то із означення об‘єднання
випливає, що характеристична властивість
об‘єднання складається з характеристичних
властивостей множин А і В за допомогою
союзу «або».
III. Закони
перетину і об‘єднання множин.
З означень перетину і об‘єднання множин
випливає для будь-яких множин А і В
справедливість рівностей
![]() і
і
![]() ,
які представляють собою запис комутативного
закону для перетину і
об‘єднання множин. Для перетину і
об‘єднання множин справедливі також
асоціативні закони:
для будь-яких множин А, В і С виконуються
рівності
,
які представляють собою запис комутативного
закону для перетину і
об‘єднання множин. Для перетину і
об‘єднання множин справедливі також
асоціативні закони:
для будь-яких множин А, В і С виконуються
рівності
![]() і
і
![]() .
Наглядно уявити асоціативний закон
можна за допомогою кругів Ейлера, а
також провести доведення цих законів.
Це пояснює, як знаходити перетин і
об‘єднання трьох множин, якщо відомо
правило для двох множин. Комутативний
і асоціативний закони множин можна
розповсюджувати на будь-яку кількість
множин. Дистрибутивний
закон: для будь-яких
множин А, В і С справедливі рівності
.
Наглядно уявити асоціативний закон
можна за допомогою кругів Ейлера, а
також провести доведення цих законів.
Це пояснює, як знаходити перетин і
об‘єднання трьох множин, якщо відомо
правило для двох множин. Комутативний
і асоціативний закони множин можна
розповсюджувати на будь-яку кількість
множин. Дистрибутивний
закон: для будь-яких
множин А, В і С справедливі рівності
![]() і
і
![]() .
Якщо в виразі існують знаки перетину і
об‘єднання і не існує дужок, то спочатку
виконують перетин, так як вважають, що
операція перетину більш «сильна», ніж
об‘єднання.
.
Якщо в виразі існують знаки перетину і
об‘єднання і не існує дужок, то спочатку
виконують перетин, так як вважають, що
операція перетину більш «сильна», ніж
об‘єднання.
IV. Доповнення
підмножини. Щоб
пояснити учням, що 5-2=3, часто використовують
такий прийом. Беруть 5 предметів (кружків),
після того, як учні впевняться за
допомогою рахунку, що кружечків дійсно
5, їм пропонують 2 кружечка прибрати і
порахувати, скільки кружечків залишилося
– 2. Нехай
![]() .
Доповненням множини В
до множини А називається
множина, яка містить ті елементи множини
А, які не належать множині В. позначають
.
Доповненням множини В
до множини А називається
множина, яка містить ті елементи множини
А, які не належать множині В. позначають
![]() .
Операція, за допомогою якої знаходять
доповнення підмножини, називається
відніманням.
Згідно з означенням доповнення
.
Операція, за допомогою якої знаходять
доповнення підмножини, називається
відніманням.
Згідно з означенням доповнення
![]() .
Якщо елементи множин А і В перелічені,
то для того, щоб знайти
.
Якщо елементи множин А і В перелічені,
то для того, щоб знайти
![]() ,
достатньо перелічити елементи, які
належать А і не належать В. Так, якщо
,
достатньо перелічити елементи, які
належать А і не належать В. Так, якщо
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
В тому випадку, коли вказані характеристичні
властивості елементів множин А і В,
характеристична властивість множини
.
В тому випадку, коли вказані характеристичні
властивості елементів множин А і В,
характеристична властивість множини
![]() має вид «
має вид «![]() ».
В запису множини
».
В запису множини
![]() нема
дужок, тому (вважають, що операція
перетину множин являється більш
«сильною», ніж віднімання) спочатку
виконують перетин множин В і С, а потім
отриману множину віднімають з множини
А..
нема
дужок, тому (вважають, що операція
перетину множин являється більш
«сильною», ніж віднімання) спочатку
виконують перетин множин В і С, а потім
отриману множину віднімають з множини
А..
V. Поняття
розбиття множин на класи.
Поняття множини і операцій над множинами
дозволяє уточнити наше уявлення про
класифікацію. Класифікація
– це дія розподілу
об‘єктів по класам на основі схожостей
об‘єктів в самому класі і їх відмінності
від об‘єктів інших класів. Як правило,
метою класифікації
являється систематизація
наших знань. Наприклад, натуральні числа
поділяються на парні і непарні; кути
бувають гострі, прямі і тупі. Будь-яка
класифікація пов‘язана з розбиттям
деякої множини на підмножини. Вважають,
що множина А розбита на
класи
![]() ,
якщо: 1) підмножини
,
якщо: 1) підмножини
![]() ,
попарно не перетинаються; 2) об‘єднання
підмножин
,
попарно не перетинаються; 2) об‘єднання
підмножин
![]() співпадає з множиною А. Якщо не виконано
хоча б одна з цих умов, класифікацію
вважають неправильною. Так, множину
трикутників можна розбити на три класи:
гострокутні, прямокутні і тупокутні.
Але не кожна система підмножин даної
множини представляє собою розбиття
цієї множини. Наприклад, якщо з множини
трикутників виділити підмножини
рівнобедрених, рівносторонніх і
різносторонніх, то розбиття множини на
класи не отримаємо. Щоб виділити
підмножину, достатньо вказати
характеристичну властивість його
елементів. Розглянемо, наприклад, множину
натуральних чисел і властивість чисел
ділитися на 3. множина розіб‘ється на
два класи: числа, кратні 3 і числа, не
кратні 3. якщо задати одночасно дві
властивості ділитися на 3 і ділитися на
5 дозволяє розбити множину на чотири
класи: числа, кратні 3 і 5; числа кратні
3 і не кратні 5; числа, кратні 5 і не кратні
3; числа, не кратні 3 і не кратних 5. Але
так відбувається не завжди, дві властивості
«бути прямокутним» і «бути тупокутним»
множину трикутників розбивають на три
класи.
співпадає з множиною А. Якщо не виконано
хоча б одна з цих умов, класифікацію
вважають неправильною. Так, множину
трикутників можна розбити на три класи:
гострокутні, прямокутні і тупокутні.
Але не кожна система підмножин даної
множини представляє собою розбиття
цієї множини. Наприклад, якщо з множини
трикутників виділити підмножини
рівнобедрених, рівносторонніх і
різносторонніх, то розбиття множини на
класи не отримаємо. Щоб виділити
підмножину, достатньо вказати
характеристичну властивість його
елементів. Розглянемо, наприклад, множину
натуральних чисел і властивість чисел
ділитися на 3. множина розіб‘ється на
два класи: числа, кратні 3 і числа, не
кратні 3. якщо задати одночасно дві
властивості ділитися на 3 і ділитися на
5 дозволяє розбити множину на чотири
класи: числа, кратні 3 і 5; числа кратні
3 і не кратні 5; числа, кратні 5 і не кратні
3; числа, не кратні 3 і не кратних 5. Але
так відбувається не завжди, дві властивості
«бути прямокутним» і «бути тупокутним»
множину трикутників розбивають на три
класи.
VI. Задачі,
пов‘язані з операціями над скінченими
множинами. В математиці
часто приходиться розв‘язувати задачі,
в яких треба визначити число елементів
або в множині, або в об‘єднанні множин,
або в доповненні підмножин. Існують
певні прийоми розв‘язку таких задач.
Умовимось позначати число елементів
скінченої множини А
![]() .
Якщо задані скінчені множини А і В, які
перетинаються,
то кількість елементів в їх об‘єднанні
підраховують за формулою
.
Якщо задані скінчені множини А і В, які
перетинаються,
то кількість елементів в їх об‘єднанні
підраховують за формулою
![]() .
Якщо ж множини А і В не
мають спільних елементів,
то число елементів в їх об‘єднанні
визначають так:
.
Якщо ж множини А і В не
мають спільних елементів,
то число елементів в їх об‘єднанні
визначають так:
![]() .
Неважко впевнитися в тому, що якщо
.
Неважко впевнитися в тому, що якщо
![]() і відомо число елементів в множинах А
і В, то число елементів в доповненні В
до А підраховують за формулою
і відомо число елементів в множинах А
і В, то число елементів в доповненні В
до А підраховують за формулою
![]() .
Розглянемо задачу: «З 40 учнів класу 34
вивчають німецьку мову, 23 – англійську,
17 – і німецьку і англійську. Чи є в класі
учні, які не вивчають ні німецьку , ні
англійську мови?». Відповідь: нема
жодного учня в класі, який би не вивчав
іноземні мови.
.
Розглянемо задачу: «З 40 учнів класу 34
вивчають німецьку мову, 23 – англійську,
17 – і німецьку і англійську. Чи є в класі
учні, які не вивчають ні німецьку , ні
англійську мови?». Відповідь: нема
жодного учня в класі, який би не вивчав
іноземні мови.
-
Декартовий добуток множин.
В початкових класах учні
розв’язують задачу: «Використовуючи
цифри 1,2,3 утворіть всілякі двозначні
числа». Такими являються
11,12,13,21,22,23,31,32,33. такі пари чисел впорядковані
(важливий порядок слідування елементів).
Впорядковану пару елементів
![]() позначають
позначають
![]() ,
де
,
де
![]() - перша координата (компонента),
- перша координата (компонента),
![]() - друга. Дві пари рівні,
якщо
- друга. Дві пари рівні,
якщо
![]() при
при
![]() .
Можна утворити впорядковані пари з
елементів різних множин. Наприклад,
.
Можна утворити впорядковані пари з
елементів різних множин. Наприклад,
![]() і
і
![]() ,
тоді
,
тоді
![]() - утворили нову множину.
- утворили нову множину.
Декартовим добутком множин
А і В називається множина пар, перша
компонента якої належить множині А,
друга – множині В. Позначають
![]() .
.
Властивості:
-
анти комутативність:
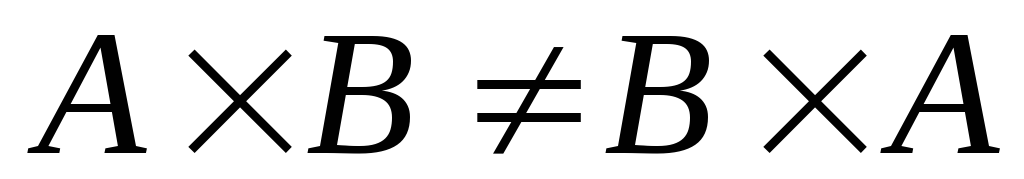 .
. -
анти асоціативність:
 .
. -
дистрибутивність до об‘єднання:
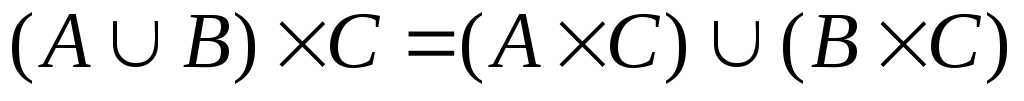 .
.
Елементи декартового добутку двох скінчених множин зручно записувати за допомогою таблиці. Наприклад, (МАЛЮНОК).
В математиці розглядають впорядковані набори з 3,4,5…елементів, які називають кортежами. Наприклад, (1,5,6) – кортеж довжини 3, (2,0,7,8,9,4) – кортеж довжиною 6.
Декартовим добутком множин
![]() називається множина кортежем довжини
називається множина кортежем довжини
![]() ,
які утворені так, що перша координата
належить множині
,
які утворені так, що перша координата
належить множині
![]() ,
друга -
,
друга -
![]() ,…,
остання -
,…,
остання -
![]() .
Позначають
.
Позначають
![]() .
.
Наприклад,
![]() ,
,
![]() ,
,
![]() ,
тоді
,
тоді
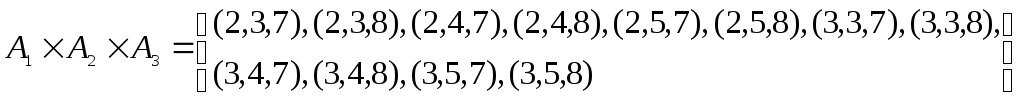 .
.
VIII. Зображення декартового добутку множин на координатній площині
Скінчені множини, які містять невелику кількість елементів, зобразити їх декартовим добуток неважко. А якщо ж множини А і В нескінчені? Круги Ейлера в цьому випадку не допоможуть. Але декартовим добуток можна зобразити на координатній площині.
Координатна пряма – це пряма із заданим на ній початком відліку і додатнім напрямком. (МАЛЮНОК). З введенням координатної прямої встановлюється зв‘язок між точками прямої і дійсними числами: кожній точці М прямої відповідає єдине дійсне число Х – координата цієї точки, і навпаки.
Розглянемо дві взаємно перпендикулярні координатні прямі: ох – абсцис і оу – ординат, з спільним початком і одиницями довжини. Площину, в якій побудовані такі вісі називають координатною площиною. ПДСК дозволяє кожній точці площини поставити в відповідність єдину пару дійсних чисел – координат цієї точки , і навпаки. З введенням координат на прямій чи на площині з‘явилась можливість розв‘язувати багато геометричних задач засобами алгебри і навпаки, алгебраїчні задачі розв‘язувати наглядно. Поняття ПДСК і координат було введено в геометрії французьким вченим і філософом Рене Декартом в XVII столітті.
Припустимо, множини А і В –
числові. Тоді елементами декартового
добутку цих множин будуть впорядковані
пари чисел. Якщо зобразити кожну пару
чисел точкою на координатній площині,
то отримаємо фігуру, яка буде наглядно
представляти декартовим добуток
![]() .
Наприклад,
.
Наприклад,
![]() і
і
![]() ,
,
![]() і
і
![]() ,
,
![]() і
і
![]() ,
,
![]() і
і
![]() ,
,
![]() і
і
![]() .
(МАЛ.)
.
(МАЛ.)
ТЕОРЕМА. Якщо
множина А містить
![]() елементів,
а множина В -
елементів,
а множина В -
![]() елементів, то декартовим добуток цих
множин містить
елементів, то декартовим добуток цих
множин містить
![]() елементів. Тобто, якщо
елементів. Тобто, якщо
![]() ,
,
![]() ,
то
,
то
![]() .
.
Правило підрахунку числа елементів декартового добутку широко використовується при розв‘язанні комбінаторних задач.
