Глава 3. Законы распределения случайной величины

Построение закона распределения - это один из наиболее простых и одновременно универсальных способов обобщения и анализа эмпирических данных, позволяющий в аналитическом виде представить их основные закономерности и внутреннюю структуру. Как известно, в математической статистике случайная величина считается заданной, если известна ее функция распределения. Этим обстоятельством определяется фундаментальное значение законов распределения. В настоящее время известно очень большое число самых разнообразных законов распределения.

Очевидно, основную их массу можно разделить на 2 группы: первая, наиболее многочисленная, включает законы распределения, которые непосредственно используются для обобщения эмпирических данных. Вторая группа – это те законы, которые применяются в статистических расчетах (например, законы Фишера, Стьюдента и др.) при построении разного рода оценок, критериев и т.п. Особое место среди всех законов распределения принадлежит нормальному закону, выведенному немецким математиком Гауссом в результате изучения им ошибок при стрельбе артиллерийскими снарядами.

3.1. Нормальный закон распределения

Случайная величина X считается распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности определяется следующей формулой:

N(m_x,_x) = f(x) = 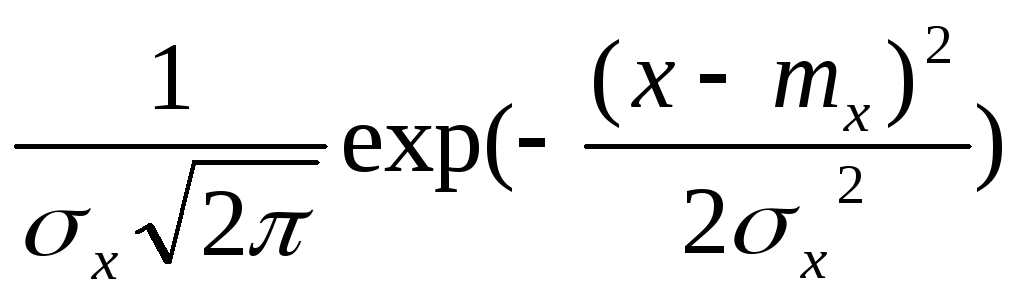. (3.1)

Как видно из данной формулы, достаточно знать всего два параметра, а именно – математическое ожидание и генеральное стандартное отклонение (m_x и _x), чтобы нормальный закон распределения считался заданным. Из формулы (3.1) следует, что нормальная кривая f(x) располагается симметрично относительно максимальной ординаты, равной f(x)_max =1/_x(2)^1/2 и проходящей через m_x (рис. 3.1). При m_x=0 нормальная кривая будет симметрична началу координат.

Если положить _x = const, но изменять параметр m_x, то кривая нормального распределения будет смещаться параллельно оси абсцисс, не меняя своей формы. При изменении параметра _x (m_x = const) происходит изменение формы кривой нормального закона. С возрастанием _x она становится все более плоской, растягиваясь вдоль оси абсцисс. При уменьшении _x, наоборот, кривая распределения сжимается с боков и вытягивается вдоль оси ординат.

Преобразуем выражение (3.1) к интегральному виду:

. (3.2)

Интеграл, входящий в эту формулу, аналитически определить нельзя, так как он через элементарные функции не выражается, но может быть вычислен путем замены переменной. Произведем замену переменной следующим образом:

t = (x  m_x)/_x,

где t - стандартизованная случайная величина, обладающая тем важным свойством, что при любом распределении случайной величины M[t]=0, D[t]=1. С учетом данной формулы имеем:

. (3.3)

Переход от величины х к t по существу означает перенос начала координат в центр распределения и выражение абсциссы в долях от стандартного отклонения. Данный интеграл, выражающий площадь под нормальной кривой в интервале [0, t], носит название функции Лапласа. Численные значения его в пределах от t=0 до t=5 приводятся в Приложении 1. Заметим, что интегральная функция нормального распределения может быть представлена через функцию Лапласа по следующей формуле:

F(x) = 0,5 + 0,5Ф[(х – m_x)/_x]. (3.4)

Перечислим свойства функции Лапласа:

Свойство 1. Функция Лапласа является нечетной, т.е. Ф(t) = Ф(t).

Свойство 2. При t=0 Ф(t)=0.

Свойство 3. При t= Ф(t)=0.5.

Поскольку удвоенная функция Лапласа равна 1, то площадь, ограниченная интегральной кривой распределения, также равна единице. Поэтому, использовав формулу (3.4), нетрудно вычислить площадь в пределах любого заданного интервала и таким образом рассчитать вероятность того, что нормально распределенная случайная величина X попадет в интервал [,].

Для симметричного относительно центра распределения интервала получим

p() = 2Ф() ,

где   некоторая заранее заданная величина. Рассчитаем теперь по этой формуле вероятность попадания X в интервалы _x, 2_x, 3_x:

p(_x  x < _x) = p|Х  m_x < _x) = 0,678,

p(2_x  x < 2_x) = p|Х  m_x < 2_x) = 0,956,

p(3_x  x < 3_x) = p|Х  m_x < 3_x) = 0,997.

Итак, с вероятностью 67,8 % возможное значение X находится в пределах  , 95,6 % - в пределах  2 и 99,7 % - в пределах  3. Поэтому можно сделать вывод, что основная часть наблюдений попадает уже в интервал  2. И лишь три наблюдения из 1000 имеют числовое значение, выходящее из интервала  3.

Естественно, что вероятность подобного события чрезвычайно мала. Это позволяет сформулировать следующее «правило трех сигм». Если распределение случайной величины неизвестно, но в интервале 3 содержится 99.7 % ее значений, то практически достоверно можно утверждать, что эта случайная величина распределена нормально. Возможно также несколько иное толкование «правила трех сигм». Если случайная величина распределена нормально, то есть основания считать, что в пределах 3 содержатся практически все ее значения. Правило трех сигм довольно широко используется в практических расчетах. Например, в теории ошибок (см. гл.5).

Основные свойства нормального закона:

Свойство 1. Плотность вероятности f(x) всегда положительна и область ее существования  < x < .

Свойство 2. Функция f(x) является четной, т.е. f(x) = f(x).

Свойство 3. Нормальная кривая не пересекается с осью x.

Свойство 4. Математическое ожидание, мода и медиана совпадают, а коэффициенты асимметрии и эксцесса равны нулю.

Свойство 5. Любое линейное преобразование исходной случайной величины X, имеющей нормальное распределение, сохраняет нормальность закона распределения.

Свойство 6. Если две независимые случайные величины X и Y распределены по нормальному закону с параметрами соответственно m_x, _x и m_y, _y, то их сумма Z = X + Y будет также иметь нормальное распределение с параметрами m_z = m_x + m_y и

_z = .

Отметим, что при переходе от генеральной совокупности к выборочным данным и соответственно от математического ожидания и генерального стандартного отклонения к их выборочным аналогам все свойства и закономерности нормального закона распределения сохраняются.

Значение нормального закона.

Главная особенность, выделяющая нормальный закон распределения среди многих других, состоит в том, что он является предельным, т.е. законом, к которому могут приближаться другие законы распределения при некоторых условиях. В частности, это вытекает из центральной предельной теоремы. Хотя существует несколько форм центральной предельной теоремы, однако все они посвящены установлению условий, при которых сумма взаимно независимых случайных величин при неограниченном увеличении числа слагаемых стремится к нормальному закону распределения. Рассмотрим центральную предельную теорему в форме теоремы Ляпунова. Суть ее состоит в следующем.

Если взаимно независимые случайные величины X₁, X₂, ..., X_n имеют конечные абсолютные центральные моменты третьего порядка и если при n выполняется условие

(3.5)

то распределение суммы случайных величин неограниченно (асимптотически) приближается к нормальному с параметрами .

Условие (3.5) выражает тот факт, что вклад всех слагаемых в рассеяние величины X по отдельности ничтожно мал по сравнению с их суммарным эффектом.

В частном случае, когда все случайные величины X₁, X₂,...,X_n имеют одинаковые законы распределения с параметрами m и , то при n условие (3.5) выполняется автоматически и, следовательно, может быть проигнорировано. Тогда в соответствии с центральной предельной теоремой распределение случайной величины становится асимптотически нормальным с параметрами m_x = nm и . При этом среднее арифметическое будет иметь асимптотически нормальное распределение с параметрами и .

Итак, когда случайная величина представляет собой результат взаимодействия большого числа сравнительно слабых и примерно равноценных факторов, то, согласно центральной предельной теореме, можно ожидать, что эта случайная величина будет распределена по нормальному закону. Однако, если среди множества взаимодействующих факторов есть хотя бы один или два преобладающих фактора, то уже нет оснований утверждать, что случайная величина будет подчиняться нормальному закону.

Заметим, что априори значение n, при котором случайная величина X становится распределенной по закону, близкому к нормальному, вряд ли может быть установлено теоретически. Однако, как показывают результаты практических расчетов, для многих природных процессов достаточно четырех-пяти равноценных факторов, чтобы распределение случайной величины стало близким к нормальному закону.

Рассмотрим конкретный пример. В соответствии с уравнением теплового баланса океана изменение температуры поверхностного слоя воды (рис. 3.2) определяется следующими основными факторами:

 - коротковолновым притоком солнечной радиации;

 - длинноволновым излучением радиации с поверхности океана;

 - затратами тепла на испарение;

 - турбулентным теплообменом между океаном и атмосферой;

 - адвекцией тепла течениями;

 - горизонтальным турбулентным теплообменом;

 - вертикальным обменом тепла с нижележащими слоями воды.

Если пренебречь рядом других факторов (например, диссипацией кинетической энергии в тепловую, тепловыми эффектами от замерзания или таяния морских льдов), то имеем семь основных факторов, влияющих на изменения температуры воды в поверхностном слое. Очевидно, что значимость указанных факторов в значительной степени зависит как от масштабов временного осреднения процессов формирования теплового баланса, так и от географического района океана.

Примем, например, период осреднения равный 1 месяцу. В этом случае для большинства районов океана преобладающим фактором оказывается годовой ход коротковолнового притока солнечной радиации, который может значительно превышать вклад в изменения температуры воды других тепловых процессов. Именно вследствие преобладания этого фактора распределение среднемесячных значений температуры поверхности океана обычно не подчиняется нормальному закону.

Естественно полагать, что годовой ход температуры обусловлен главным образом годовым ходом солнечной радиации. Для исключения влияния радиации можно рассчитать аномалии температуры воды

∆t_ij = t_ij t_j , i=1,…,n j=1,…,m.

где n – количество лет, m – количество месяцев (m=12), t_j - среднемноголетняя норма температуры для j-го месяца. В результате такой процедуры обычно принимается, что в аномалиях температуры воды уже отсутствует годовой цикл солнечной радиации. В этом случае вклад различных факторов в формирование температуры воды в большинстве районов океана становится более равноценным. Поэтому распределение аномалий среднемесячных величин температуры воды значительно чаще подчиняется нормальному закону.

Отметим, что если в качестве масштаба временного осреднения взять 1 год, то в этом случае радиационный фактор уже, как правило, не дает преобладающего вклада в колебания температуры поверхности океана. Поэтому распределение средних годовых значений температуры в отличие от среднемесячных величин носит значительно более симметричный характер.

Помимо центральной предельной теоремы, важное значение нормального закона

состоит также в том, что он хорошо разработан теоретически, доступен и широко используется при решении многочисленных задач. В математической статистике нормальный закон играет роль некоторого стандарта, с которым сравниваются другие распределения. Кроме того, он широко используется во многих статистических методах анализа информации: методе наименьших квадратов, корреляционном анализе, проверке статистических гипотез, методе ошибок и др.

В связи с этим проверка гипотезы нормальности распределения исходной выборки, т.е. степени соответствия эмпирического распределения нормальному, представляет собой один из важнейших этапов первичной обработки исходных данных.

Пример 3.1. На рис. 3.3 представлены гистограммы среднемесячных значений температуры поверхности океана и их аномалий для района Канарского апвеллинга, ограниченного по широте 20 и 24^о с.ш. и по долготе 20^о з.д. и берегом Африки. Нетрудно видеть, что распределение среднемесячных значений ТПО является двухмодальным и, естественно, абсолютно не соответствует нормальному закону распределению. В то же время распределение аномалий ТПО кардинально отличается от распределения среднемесячных значений ТПО и уже носит симметричный характер, т.е. очень близко к нормальному распределению. Таким образом, можно считать установленным исключение превалирующего влияния потока суммарной радиации на годовой ход ТПО, вследствие чего вклад различных факторов в формирование температуры воды становится относительно равноценным.