2.9. Построение опорного плана

Рассмотрим сначала частный случай ограничений типа «меньше или равно», использованных при построении модели оптимального планирования производства. После приведения к каноническому виду система ограничений будет:

Про такую систему говорят, что она имеет предпочтительный вид, поскольку выполняются два условия:

1. Правые части ограничений-равенств неотрицательны (для рассматриваемой задачи это объемы имеющихся ресурсов).

2. Каждое ограничение содержит предпочтительную переменную, входящую в него с коэффициентом, равным единице, и не входящую в остальные ограничения (для приведенного примера это , где .

Для такой системы ограничений всегда можно найти опорное решение, если принять предпочтительные переменные за базисные, а остальные считать свободными и приравнять нулю. Тогда базисные переменные равны правым частям ограничений-равенств и опорный план будет:

.

Экономический смысл такого плана очевиден: производство отсутствует, все ресурсы зарезервированы. Он будет оптимален только в тривиальном случае, когда все виды продукции являются убыточными.

В общем случае любую задачу линейного программирования можно преобразовать к каноническому виду:

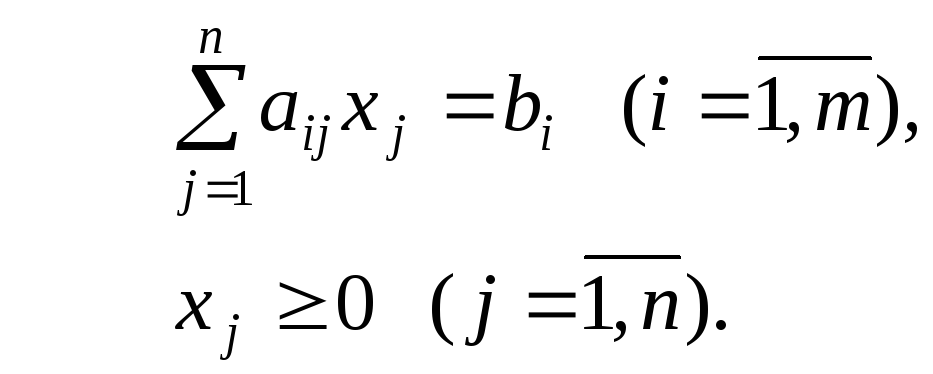
Без ограничения общности можно считать, что правые части ограничений-равенств неотрицательны, иначе соответствующие ограничения было бы достаточно умножить на –1, но предполагать предпочтительный вид даже для отдельных ограничений оснований нет.

Наиболее общим способом построения опорного плана является использование искусственных переменных , которые добавляются ко всем левым частям ограничений-равенств, не имеющих предпочтительного вида. В частности, для модели формирования минимальной продовольственной корзины получим:

Если эти искусственные переменные приравнять правым частям ограничений, то при таком опорном плане затраты на приобретение продуктов минимальны (равны нулю), что было бы хорошо, но вот только корзина будет пустая, а это уже неприемлемо.

Чтобы в последующих итерациях освободиться от искусственных переменных, введем для каждой из них достаточно большой штраф в выражении для целевой функции. Если решается задача на максимум, то переменной в функционале должно соответствовать слагаемое , где , а при решении задачи на минимум выражение – .

Такой метод называют M-методом, или методом больших штрафов, а полученную задачу – M-задачей, соответствующей исходной. Естественно ожидать, что все искусственные переменные в процессе оптимизации получат нулевые значения. Однако, если исходная задача несовместна, то при любом штрафе исключить все искусственные переменные не удастся. Например, если задачу оптимального планирования производства дополнить условиями по минимальным объемам производства отдельных видов продукции, то при недостатке наличных ресурсов придется приобретать их по любой цене. Зато сразу видно, что задача не имеет допустимого решения и более того видно, сколько и каких именно ресурсов не хватает.

Остается открытым вопрос, как понимать термин «достаточно большой». Теоретически надо . При аналитических вычислениях пишут M, и при обнулении искусственных переменных соответствующее выражение исчезает.

При компьютерных вычислениях всегда имеют место ошибки округления, особенно, когда в операциях сложения или вычитания одновременно участвуют и большие, и малые числа. В этом легко убедиться экспериментом, вычисляя, например, значение 10¹⁵ + 1. Скорее всего, единица просто не будет прибавлена. Если это не так, то достаточно увеличить первое или уменьшить второе число. Поэтому лучше не следовать бездумно теоретическому требованию о «большом значении» M, а назначать его исходя из «разумной достаточности». Если же в решение необоснованно войдет искусственная переменная, то соответствующий ей штраф можно увеличить.

В реальных компьютерных программах, реализующих симплекс-метод, для подавления ошибок округления используется двухэтапный метод. На первом этапе решается M-задача, но за критерий принимается просто сумма значений искусственных переменных. Если достигается нулевое значение этой суммы, то переходят ко второму этапу, принимая полученное оптимальное решение за опорный план исходной задачи. Если же на первом этапе целевая функция не обнуляется, следовательно, исходная система ограничений несовместна.