
- •Практическое занятие n 15
- •" Вычисление двойных интегралов "
- •Практическое занятие № 15 " Вычисление двойных интегралов "
- •Краткая теория.
- •1. Двойной интеграл в прямоугольных координатах
- •2. Основные свойства двойного интеграла
- •3. Правила вычисления двойных интегралов
- •4. Примеры вычислений двойных интегралов.
- •Задания
- •Карта полученных результатов
- •6.Ответить на контрольные вопросы.
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РФ
ГОУ
МИАССКИЙ ЭЛЕКТРОМЕХАНИЧЕСКИЙ ТЕХНИКУМ
РАССМОТРЕНО
на
заседании цикловой комиссии
спец.
“Естественно-научных дисцип.”
Протокол
№____ от ________2004г.
Председатель
цикловой комиссии
______________/С.В.Скоробогатова
/
УТВЕРЖДАЮ
Зам.директора
по УПР
_______/И.В.Карпов/
“____”________2004г.
по
дисциплине
МАТЕМАТИКА
Курс
II
Специальность
(все технические)
Разработал:________/Н.И.Буяндуков/
2004
г.
Цель:
Научиться алгоритму нахождения двойных
интегралов.
Оборудование:
Карточки-задания, микрокалькулятор,
линейка, карандаш.
Порядок
выполнения практического занятия.
1.
Ознакомиться с кратким теоретическим
содержанием для выполнения практического
занятия.
2.
Выполнить предложенные задания.
3.
Результаты, полученные при выполнении
заданий, занести в таблицу.
4.
Ответить на контрольные вопросы.
Пусть
функция f(х,y) определена в ограниченной
замкнутой области D плоскости хОy.
Разобъем область D произвольным образом
на n элементарных областей, имеющих
площади
Интегральной
суммой для функции f(х,y) по области D
называется сумма вида:
Двойным
интегралом
от функции f(х,y) по области D называется
предел интегральной суммы при условии,
что наибольший из диаметров элементарных
областей стремится к нулю:
Если
функция f(х;y) непрерывна в замкнутой
области D, то предел интегральной суммы
существует и не зависит от способа
разбиения области D на элементарные и
от выбора точек Pi
.
Если
f(х,y)>0 в области D, то двойной интеграл
1.
2.
3.
Если область интегрирования D разбита
на две области D1
и D2,
то
В
декартовых координатах двойной интеграл
обычно записывают в виде
Различают
два основных вида области интегрирования.
1.
Область интегрирования D ограничена
слева и справа прямыми х=a и х=b (причем
a<b), а снизу и сверху – непрерывными
кривыми
(рис.1)
Для
такой области двойной интеграл
вычисляется по формуле
причем
сначала вычисляется интеграл f(х,y) dy, в
котором х считается постоянным.
Итак
для того, чтобы вычислить интеграл по
формуле (5) необходимо:
1).
сначала вычислить определенный интеграл
-
-
Результатом
вычисления внутреннего интеграла
является функция, зависящая только от
х.
2)
полученную функцию от х теперь повторно
интегрируем в границах от a до b и таким
образом получаем значение двойного
интеграла.
Замечание:
В формуле (5) границы внешнего интеграла
всегда постоянны, т.е. не зависят от
переменных х и у.
Пример
1: Вычислить двойной интеграл
Решение:
1.
Интегрируем сначала по переменной у в
пределах от –х до х, считая, что во
внутреннем интеграле х - соnst
2.
А теперь интегрируем по переменной х
в пределах от 0 до 1, функцию
Для
сокращения записи все вычисления
можно записать следующим образом:
Ответ:
Пример
2: Вычислить двойной интеграл
Решение:
Ответ:
0,9
Пример
3: Вычислить двойной интеграл
Решение:
Ответ:
7
Пример
4: Вычислить двойной интеграл
Решение:
Построим
данные прямые на декартовой координатной
плоскости
(рис.2)
Ответ:
Пример
5: Вычислить двойной интеграл
Решение:
Построим
данные прямые на декартовой координатной
плоскости
(рис.3)
Задание
1. Вычислить двойной интеграл:
№
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
2. Вычислить двойной интеграл:
№
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
3. Вычислить двойной интеграл по
прямоугольной области D, ограниченной
прямыми №
варианта
Двойной
интеграл, ограниченный прямыми
№ варианта
Двойной
интеграл, ограниченный прямыми
Вариант
1
где
х= -1, х=2, у=0 и у=4
Вариант
9
где
х= -1, х=4, у=0 и у=4
Вариант
2
где
х= -1, х=3, у=0 и у=3
Вариант
10
где
х= -1, х=5, у=0 и у=3
Вариант
3
где
х= -1, х=4, у=0 и у=2
Вариант
11
где
х= -1, х=6, у=0 и у=2
Вариант
4
где
х= -1, х=5, у=0 и у=1
Вариант
12
где
х= -1, х=1, у=0 и у=1
Вариант
5
где
х= -1, х=6, у=0 и у=4
Вариант
13
где
х= -1, х=2, у=0 и у=4
Вариант
6
где
х= -1, х=1, у=0 и у=3
Вариант
14
где
х= -1, х=3, у=0 и у=3
Вариант
7
где
х= -1, х=2, у=0 и у=2
Вариант
15
где
х= -1, х=4, у=0 и у=2
Вариант
8
где
х= -1, х=3, у=0 и у=1
Вариант
16
где
х= -1, х=4, у=0 и у=1
Задание
4. Вычислить двойной интеграл по
прямоугольной области D, ограниченной
прямыми №
варианта
Двойной
интеграл, ограниченный прямыми
№ варианта
Двойной
интеграл, ограниченный прямыми
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
5. Вычислить двойной интеграл , где
областью интегрирования - является
треугольник, ограниченный прямыми №
варианта
Двойной
интеграл, ограниченный прямыми
№ варианта
Двойной
интеграл, ограниченный прямыми
Вариант
1
где
y=0, х=1 и у=2x
Вариант
9
где
y=0, х=1 и у=4x
Вариант
2
где
y=0, х=2 и у=2x
Вариант
10
где
y=0, х=2 и у=4x
Вариант
3
где
y=0, х=3 и у=2x
Вариант
11
где
y=0, х=3 и у=4x
Вариант
4
где
y=0, х=4 и у=2x
Вариант
12
где
y=0, х=4 и у=4x
Вариант
5
где
y=0, х=1 и у=3x
Вариант
13
где
y=0, х=1 и у=5x
Вариант
6
где
y=0, х=2 и у=3x
Вариант
14
где
y=0, х=2 и у=5x
Вариант
7
где
y=0, х=3 и у=3x
Вариант
15
где
y=0, х=3 и у=5x
Вариант
8
где
y=0, х=4 и у=3x
Вариант
16
где
y=0, х=4 и у=5x
№ задания
Результаты
выполненных заданий (ответы) Задание
1
Задание
2
Задание
3
Задание
4
Задание
5
Контрольные
вопросы:
1.
Что называется интегральной суммой ?
2.
Дать определение двойного интеграла
.
3.
В чем заключается геометрический смысл
двойного интеграла ?
4.
Описать алгоритм нахождения двойного
интеграла .
5.
Перечислить свойства двойных интегралов.
Отчет
о проделанной работе.
1.Цель
работы.
2.Задание.
3.Выписать
формулы, необходимые для вычислений.
4.Описание
решения заданий.
5.Оформить
карту полученных результатов ( внести
ответы ).
16
Практическое занятие n 15
" Вычисление двойных интегралов "
Практическое занятие № 15 " Вычисление двойных интегралов "
Краткая теория.
1. Двойной интеграл в прямоугольных координатах
![]() ,
,
![]() ,
…
,
…
![]() ,
и диаметры d1
,d2
,...,dn
(диаметром области называется наибольшее
из расстояний между двумя точками
границы этой области). Выберем в каждой
элементарной области произвольную
точку Pi
(хi;
уi)
и умножим значение функции в точке Pi
на площадь этой области.
,
и диаметры d1
,d2
,...,dn
(диаметром области называется наибольшее
из расстояний между двумя точками
границы этой области). Выберем в каждой
элементарной области произвольную
точку Pi
(хi;
уi)
и умножим значение функции в точке Pi
на площадь этой области.![]()
![]() (1)
(1)![]() равен объему цилиндрического тела,
ограниченного сверху поверхностью
z=f(х,y), сбоку цилиндрической поверхностью
с образующими, параллельными оси Oz, и
снизу областью D плоскости хOy.
равен объему цилиндрического тела,
ограниченного сверху поверхностью
z=f(х,y), сбоку цилиндрической поверхностью
с образующими, параллельными оси Oz, и
снизу областью D плоскости хOy.2. Основные свойства двойного интеграла
![]() (2)
(2)![]() ,
где с -постоянная (3)
,
где с -постоянная (3)![]() (4)
(4)![]() .
.3. Правила вычисления двойных интегралов
![]() и
и
![]() ,
где
,
где
![]() <
<![]() ,
каждая из которых пересекаются
вертикальной прямой только в одной
точке (рис.1)
,
каждая из которых пересекаются
вертикальной прямой только в одной
точке (рис.1)
 (5)
(5) ,считая х - постоянным числом (или говорят
вычислить внутренний интеграл), где
,считая х - постоянным числом (или говорят
вычислить внутренний интеграл), где
![]() - нижняя граница интегрирования;
- нижняя граница интегрирования;
![]() ,
- верхняя граница интегрирования.
,
- верхняя граница интегрирования.
4. Примеры вычислений двойных интегралов.
![]()

![]()
![]()

![]()
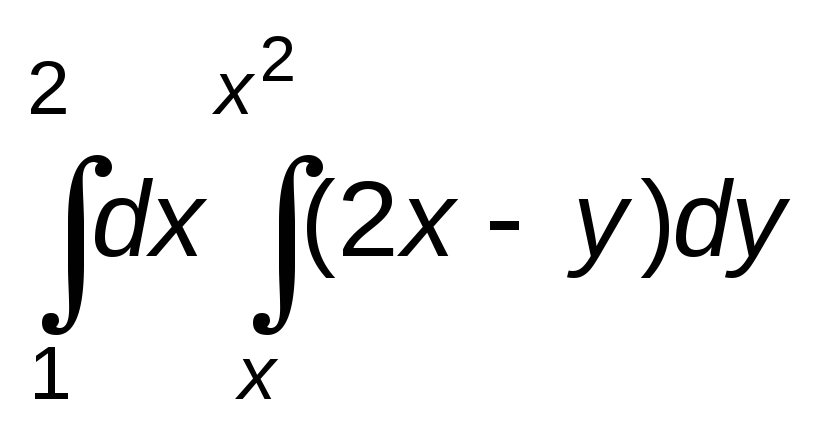

![]() по прямоугольной области D, ограниченной
прямыми х = 1,х = 2,у = 0 и у = 2,
по прямоугольной области D, ограниченной
прямыми х = 1,х = 2,у = 0 и у = 2,
![]() если областью интегрирования является
прямоугольник, ограниченный прямыми
у=1 и у=2 (
если областью интегрирования является
прямоугольник, ограниченный прямыми
у=1 и у=2 (![]() ),
х=0 и х=4 (
),
х=0 и х=4 (![]() ).
).

![]()
![]() если областью интегрирования является
треугольник, ограниченный прямыми у=0,
х=2 и
если областью интегрирования является
треугольник, ограниченный прямыми у=0,
х=2 и
![]()

 Ответ:
Ответ:
![]()
Задания
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
















![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Карта полученных результатов
6.Ответить на контрольные вопросы.
1
2
15
3
14
4
13
5
12
6
11
7
10
8
9
