
- •Тема "Вычисление определенных интегралов непосредственным интегрированием и методом подстановки"
- •Краткая теория.
- •1. Определение определенного интеграла
- •2. Основные свойства определенного интеграла.
- •3. Интегрирование определенных интегралов
- •Таким образом, имеем
- •Задания
- •Карта полученных результатов
- •6. Ответить на контрольные вопросы.
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РФ
ГОУ
МИАССКИЙ ЭЛЕКТРОМЕХАНИЧЕСКИЙ ТЕХНИКУМ
РАССМОТРЕНО
на
заседании цикловой комиссии
спец.
“Естественно-научных дисц.”
Протокол
N____
от ________2003г.
Председатель
цикловой комиссии
__________________/А.П.Пинаева
/
УТВЕРЖДАЮ
Зам.директора
по УПР
_______/И.В.Карпов/
“____”________2003г.
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ N
11
(для
технических специальностей)
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ N
9
(для
экономических специальностей)
по
дисциплине
МАТЕМАТИКА
"Вычисление
определенных интегралов
непосредственным
интегрированием и методом подстановки"
Курс
II
Специальности
(все)
Разработал:________/Н.И.Буяндуков/
2003
г.
Цели:
1. Научиться алгоритму нахождения
определенного интеграла непосредственным
интегрированием.
2.
Научиться алгоритму нахождения
определенного интеграла методом
подстановки.
Оборудование:
Карточки-задания, микрокалькулятор,
линейка, карандаш.
Порядок
выполнения практического занятия.
1.
Ознакомиться с кратким теоретическим
содержанием для выполнения практического
занятия.
2.
Выполнить предложенные задания.
3.
Результаты, полученные при выполнении
заданий, занести в таблицу.
4.
Ответить на контрольные вопросы.
Определенным
интегралом
(интегралом)
от функции f(х) на отрезке [a,b] называется
приращение первообразной F(х) этой
функции и обозначается: Эта
формула (1) называется формулой
Ньютона - Лейбница. Для
любой функции f(х), непрерывной на отрезке
[a,b], всегда существует определенный
интеграл
1.
Определенный интеграл от алгебраической
суммы конечного числа функций равен
алгебраической сумме определенных
интегралов от слагаемых функций: 2.
Постоянный множитель можно выносить
за знак определенного интеграла: 3.
При перестановке пределов интегрирования
определенный интеграл меняет знак на
противоположный: 4.
Определенный интеграл с одинаковыми
пределами равен нулю: 5.
Отрезок интегрирования можно разбивать
на части: Для
вычисления определенного интеграла
от функции f(х) в том случае, когда можно
найти соответствующий неопределенный
интеграл F(х), служит формула
Ньютона-Лейбница: т.е.
определенный интеграл равен разности
значений первообразной при верхнем и
нижнем пределах интегрирования.
Примеры:
Найти следующие интегралы:
методом
замены переменной(метод подстановки).
При
вычислении определенного интеграла
методом замены переменной (способом
подстановки) определенный интеграл
При
этом старые пределы интегрирования a
и b заменяются соответственно новыми
пределами интегрирования
и ,
которые находятся из основной подстановки.
Из
первой подстановки новые пределы
интегрирования вычисляются =g(а)
и =g(b).
Из
второй подстановки новые пределы
интегрирования находятся путем решения
уравнений a=g()
и b=g()
относительно
и .
Примеры:
Найти следующие интегралы:
Обозначим
Далее
находим пределы интегрирования по
новой переменной t, которые определяются
из значения подъинтегральной функции,
где вместо х подставляем значения 2 и
3.
Находим
нижний предел
Подставим
найденные значения t и
Обозначим
Далее
находим пределы интегрирования по
новой переменной t, которые определяются
из значения подъинтегральной функции,
где вместо х подставляем значения 1 и
2.
Находим
нижний предел
Подставим
найденные значения t и
Обозначим
Находим
нижний предел
Таким
образом
Обозначим
Находим
нижний предел
Итак
Обозначим
Находим
нижний предел
Таким
образом
Обозначим
Находим
нижний предел
Таким
образом
Обозначим
Находим
нижний предел
Итак
имеем интеграл
Обозначим
Находим
нижний предел
Таким
образом
Задание
1.
Найти следующие интегралы: №
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
2.
Найти следующие интегралы: № варианта
Исходные
данные
№ варианта
Исходные
данные Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
3.
Найти следующие интегралы: №
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
4.
Найти следующие интегралы: №
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
5.
Найти следующие интегралы: №
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
6.
Найти следующие интегралы: №
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
7.
Найти следующие интегралы: №
варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
8.
Найти следующие интегралы: № варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
9.
Найти следующие интегралы: № варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
10.
Найти следующие интегралы: № варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
11.
Найти следующие интегралы: № варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
Задание
12.
Найти следующие интегралы: № варианта
Исходные
данные
№ варианта
Исходные
данные
Вариант
1
Вариант
9
Вариант
2
Вариант
10
Вариант
3
Вариант
11
Вариант
4
Вариант
12
Вариант
5
Вариант
13
Вариант
6
Вариант
14
Вариант
7
Вариант
15
Вариант
8
Вариант
16
№ задания
Результаты
выполненных заданий (ответы) Задание
1
Задание
2
Задание
3
Задание
4
Задание
5
Задание
6
Задание
7
Задание
8
Задание
9
Задание
10
Задание
11
Задание
12
Контрольные
вопросы: 1.
Какая функция называется определенным
интегралом ? 2.
Перечислить основные свойства
определенных интегралов? 3.
В чем заключается сущность метода
непосредственного интегрирования
неопределенных интегралов. 4.
Назвать формулу Ньютона - Лейбница? 5.
В чем заключается сущность интегрирования
определенных интегралов методом замены
переменной (подстановки)?
6.
Описать алгоритм интегрирования
определенных интегралов методом замены
переменной?
7.
Что называется дифференциалом функции
у=f(х)?
8.
Для чего необходимо введение новой
переменной?
9.
Относительно какой переменной вычисляется
табличный интеграл?
10.
Как определяются новые пределы
интегрирования?
Отчет
о проделанной работе.
1.
Цель работы.
2.
Задание.
3.
Выписать формулы, необходимые для
вычислений.
4.
Описание решения заданий.
5.
Оформить карту полученных результатов
(внести ответы).
20
Тема "Вычисление определенных интегралов непосредственным интегрированием и методом подстановки"
Краткая теория.
1. Определение определенного интеграла
![]() (1)
(1)![]() .
.2. Основные свойства определенного интеграла.
![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)![]()
![]()


![]()
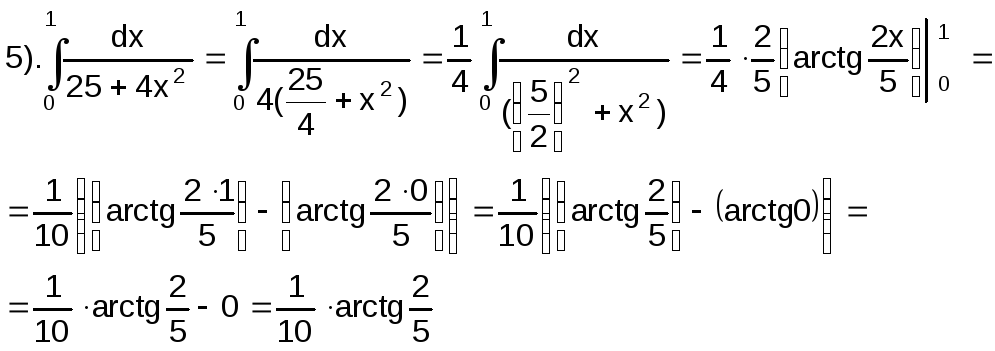
3. Интегрирование определенных интегралов
![]() преобразуется с помощью подстановки
t=g(х) в определенный интеграл относительно
новой переменной t.
преобразуется с помощью подстановки
t=g(х) в определенный интеграл относительно
новой переменной t.Таким образом, имеем
![]() (7)
(7)![]() .
.![]() ,
тогда найдем дифференциал функции
,
тогда найдем дифференциал функции![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.![]() ,
и новые пределы интегрирования
и
в исходный интеграл и, тогда получим
,
и новые пределы интегрирования
и
в исходный интеграл и, тогда получим .
.![]() .
.![]() ,
далее находим дифференциал функции
,
далее находим дифференциал функции![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
Таким образом
.
Таким образом![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.![]() ,
и новые пределы интегрирования
и
в исходный интеграл и, тогда получим
,
и новые пределы интегрирования
и
в исходный интеграл и, тогда получим .
.![]() .
.![]() ,
далее находим дифференциал функции
,
далее находим дифференциал функции![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.
![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
. .
.![]() .
.![]() ,
тогда найдем дифференциал функции
,
тогда найдем дифференциал функции![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.
![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.
![]() .
.![]() ,
далее находим дифференциал функции
,
далее находим дифференциал функции![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.
![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.
![]() .
.![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.
![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.![]()
![]() .
.![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.
![]() .
.![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() .
.
![]() ,
тогда верхний предел
,
тогда верхний предел
![]() .
.
Задания
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()








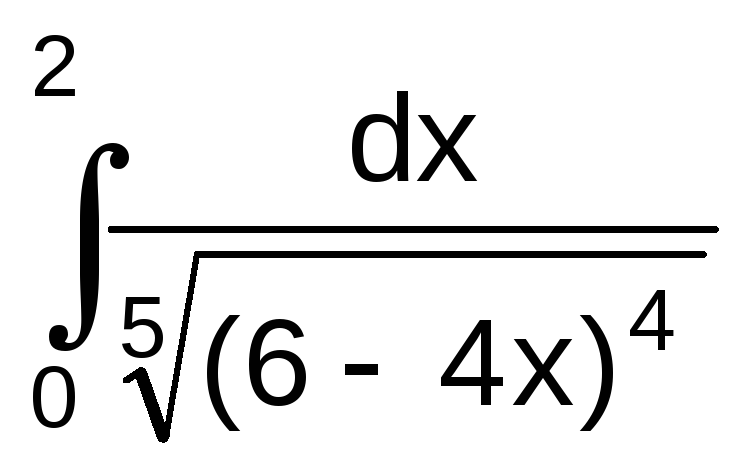







![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Карта полученных результатов
6. Ответить на контрольные вопросы.

2 19

3 18
4 17
5 16
6 15
7 14
8 13
9 12
10 11
