
- •Численные методы,
- •Введение
- •1. Абсолютная и относительная погрешности.
- •1.1. Число верных знаков приближенного числа
- •1.2. Погрешность функций
- •1.3. Погрешность простейших функций двух переменных
- •1.4. Примеры и задания
- •2. Приближение функций
- •2.1. Интерполяционные полиномы
- •2.2. Интерполяционный полином Лагранжа
- •2.3. Интерполяционный полином Ньютона
- •2.3. Примеры и задания для практических занятий
- •Второй интерполяционный полином Ньютона:
- •3. Численные методы решений трансцендентных и алгебраических уравнений
- •3.1. Метод простой итерации для решения нелинейных и трансцендентных уравнений
- •3.2. Метод хорд и секущих
- •3.3. Метод касательных
- •Скорость сходимости итерационных методов
- •Условие выхода из вычислительного процесса по заданной точности в методах простой итерации
- •Пример и задание для практических занятий
- •4. Численное интегрирование
- •4.1. Метод Ньютона – Котеса
- •4.2. Метод прямоугольников.
- •4.3. Метод трапеций
- •4.4. Метод парабол. (Метод Симпсона)
- •4.5. Квадратурные формулы Гаусса
- •4.6. Задание для практических занятий
- •Численные методы линейной алгебры
- •5.1. Численное решение слау
- •5.2. Прямые методы решения слау
- •5.2.1. Метод Гаусса (Метод исключений)
- •5.2.2. Вычислительная схема метода Гаусса
- •5.2.3. Ортогонализация матриц
- •5.2.4. Решение системы уравнений методом ортогонализации
- •5.3. Итерационные методы решения слау
- •5.3.1. Метод простой итерации
- •5.3.2. Метод Якоби и метод Зейделя
- •5.3.3. Метод оптимального спектрального параметра (осп) для простой итерации
- •5.4. Нахождение собственных векторов и собственных значений матриц
- •5.5. Примеры и задания к теме
- •5.5.1. Прямые методы решения слау
- •5.5.2. Итерационные методы решения слау
- •5.5.3. Нахождение собственных значений и векторов
- •6. Численные методы решения обыкновенных дифференциальных уравнений
- •6.1. Метод разложения в ряд Тейлора
- •6.2. Общая схема метода Рунге - Кутта
- •6.3 Методы Рунге-Кутта низших порядков
- •6.3.1 Метод Эйлера
- •6.3.2. Метод трапеций и прямоугольника
- •6.4. Методы Рунге-Кутта высших порядков
- •6.5. Задание к теме и пример решения оду
- •Численное решение начально-краевых задач для дифференциальных уравнений в частных производных
- •Конечные разности.
- •Гиперболические уравнения
- •Параболические уравнения
- •Уравнения эллиптического типа
- •7.4.1. Разностная схема уравнений
- •Лабораторные задания к теме «Численное решение уравнений в частных производных»
- •7.5.1. Гиперболические уравнения
- •7.5.2. Параболические уравнения
- •7.5.3. Эллиптические уравнения
- •Литература
- •Содержание
-
Параболические уравнения
Данный
тип уравнений рассмотрим на примере
одномерного нестационарного уравнения
теплопроводности (7.3.1) с граничными
(7.3.2) и начальными условиями (7.3.3),
описывающего процесс установления
температуры в изолированном стержне,
имеющем на концах постоянную температуру
![]() и
и
![]() и заданное начальное распределение
температуры вдоль стержня
и заданное начальное распределение
температуры вдоль стержня
![]() :
: ![]()
![]() ,
, ![]() (7.3.1)
(7.3.1)
![]() ,
, ![]() ,
, ![]() (7.3.2)
(7.3.2)
![]()
![]() (7.3.3)
(7.3.3)
Для аппроксимации уравнения (7.3.1) используем конечные разности (7.1.2) и (7.1.4)
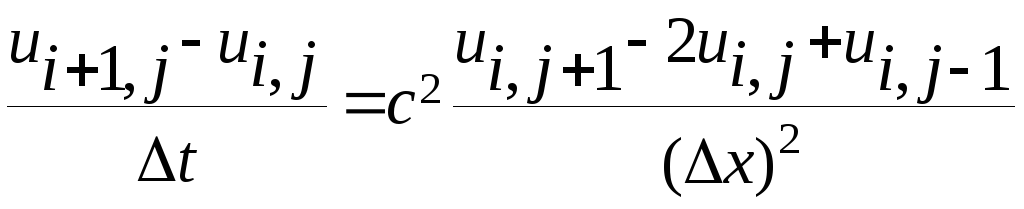
Обозначим
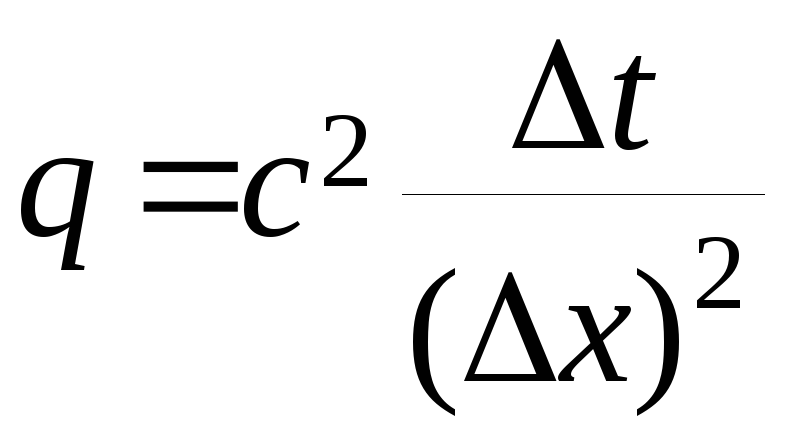 .
После преобразований получаем явную
четырехточечную сеточную схему, в
которой значение функции на
.
После преобразований получаем явную
четырехточечную сеточную схему, в
которой значение функции на
![]() слое по времени выражается через три
соседних значения на нижнем,
слое по времени выражается через три
соседних значения на нижнем,
![]() -ом слое:
-ом слое:
![]() (7.3.4)
(7.3.4)
Формула
(7.3.4) позволяет последовательно найти
все значения сеточной функции, начиная
со слоя
![]() ,
на котором заданы начальные условия
(7.3.3). Однако вычисления по этой формуле
устойчивы только в том случае, если
выполняется условие
,
на котором заданы начальные условия
(7.3.3). Однако вычисления по этой формуле
устойчивы только в том случае, если
выполняется условие
![]() .
Это накладывает жесткие ограничения
на шаг сетки по времени, обязывая выбирать
этот шаг намного меньшим, чем шаг по
пространственной координате, что
существенно увеличивает время расчета
и ограничивает применимость явной
схемы.
.
Это накладывает жесткие ограничения
на шаг сетки по времени, обязывая выбирать
этот шаг намного меньшим, чем шаг по
пространственной координате, что
существенно увеличивает время расчета
и ограничивает применимость явной
схемы.
Для аппроксимации уравнения (7.3.1) может быть использована левая конечная разность (7.1.2)
 ,
что приводит к неявной четырёхточечной
разностной схеме
,
что приводит к неявной четырёхточечной
разностной схеме 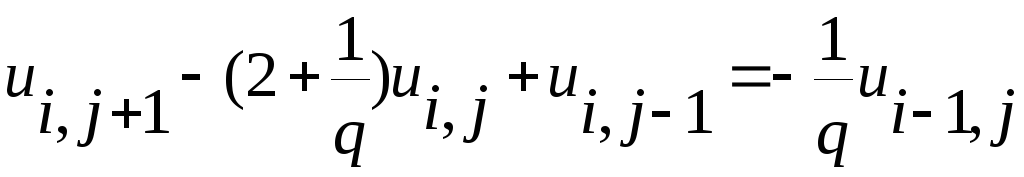 ,
(7.3.5) которая устойчива при любых
соотношениях шагов сетки.
,
(7.3.5) которая устойчива при любых
соотношениях шагов сетки.
Из
(7.3.5) следует, что для каждого слоя
![]() по времени значения неизвестной сеточной
функции
по времени значения неизвестной сеточной
функции
![]() ,
,
![]() связаны СЛАУ с трехдиагональной матрицей.
В этой матрице на главной диагонали
находится значение
связаны СЛАУ с трехдиагональной матрицей.
В этой матрице на главной диагонали
находится значение
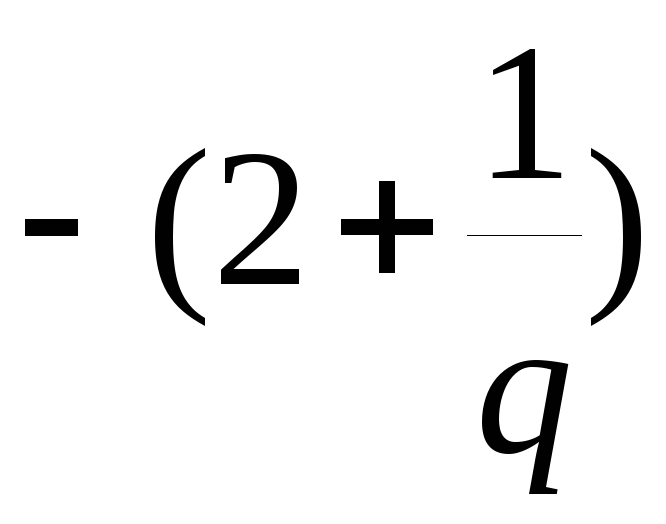 ,
а на двух соседних диагоналях -
,
а на двух соседних диагоналях -![]() .
Значение на главной диагонали близко
к
.
Значение на главной диагонали близко
к
![]() ,
т.к. значение
,
т.к. значение
![]() ,
как правило,
,
как правило,
![]() .
Вектор в правой части (7.3.5)(при постоянном
значении
.
Вектор в правой части (7.3.5)(при постоянном
значении
![]() )
известен из вычислений на предыдущем
шаге по времени и входит в правую часть
СЛАУ.
)
известен из вычислений на предыдущем
шаге по времени и входит в правую часть
СЛАУ.
Последовательно
решая СЛАУ (7.3.5), начиная со слоя
![]() ,
можно вычислить сеточную функцию во
всей области решения. Система (7.3.5) может
быть решена как стандартным методом (
т.к. порядок системы не слишком велик -
,
можно вычислить сеточную функцию во
всей области решения. Система (7.3.5) может
быть решена как стандартным методом (
т.к. порядок системы не слишком велик -
![]() ), так и специальными методами применяемыми
для решения систем с трехдиагональными
матрицами, например, методом прогонки
[2].
), так и специальными методами применяемыми
для решения систем с трехдиагональными
матрицами, например, методом прогонки
[2].
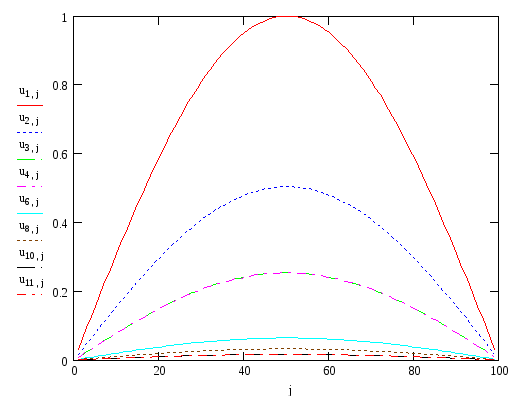
рис.2
На
рис.2 представлен расчет установления
температуры в стержне, проведенный по
неявной схеме (7.3.5), при следующих
начальных и граничных условиях: ![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
, ![]() .
Шаги сетки по времени и по пространственной
координате
.
Шаги сетки по времени и по пространственной
координате
![]() ,
,
![]() .
При данном значении
.
При данном значении
![]() расчеты по явной схеме (7.3.4) были бы
невозможны из-за большой неустойчивости.
Число шагов по
расчеты по явной схеме (7.3.4) были бы
невозможны из-за большой неустойчивости.
Число шагов по
![]() и по
и по
![]() соответственно M=10,
N=100.
соответственно M=10,
N=100.
-
Уравнения эллиптического типа
Двумерные
краевые задачи для уравнений данного
типа рассмотрим на примере уравнений
Лапласа, Пуассона и Гельмгольца.
Обозначим, как обычно, оператор
Лапласа
![]()
![]()
Тогда
указанные уравнения имеют вид: 1.Уравнение
Лапласа
![]() 2.Уравнение
Пуассона
2.Уравнение
Пуассона
![]() 3.Уравнение
Гельмгольца
3.Уравнение
Гельмгольца
![]()
Граничные
условия задаются на границе области
![]() :
: ![]() ,в
частности, на границе прямоугольника
,в
частности, на границе прямоугольника
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
