1.3 Расчет динамической характеристики

Динамическая характеристика находится по интегральной передаточной функции , которая рассчитывается как пространственная композиция от произведения континуальной передаточной функции на преобразованную по Лапласу стандартизирующую функцию с выделенным из нее входным воздействием. Так как стандартизирующая функция не содержит входное воздействие f(x,t):

; (11)

; (12)

. (13)

Интегральную передаточную функцию представим в виде:

. (14)

Слагаемые и найдем как:

; (15)

; (16)

Из уравнений (14), (15), (16) получим:

(17)

Для выбранной выходной переменной построим ЛАЧХ. При этом необходимо получить частотную форму записи передаточной функции (17), для чего произведем замену р=j

; (18)

Найдем ЛАЧХ по выражению:

. (19)

Для построения характеристики используем программу MathCad:

L(ω)

Рисунок 3 – График логарифмической амплитудно-частотной характеристики

Аппроксимируя полученную ЛАЧХ ее стандартными типовыми наклонами получаем 0 дб/дек и -20 дб/дек, что соответствует апериодическому звену 1-го порядка. Тогда передаточная функция будет иметь вид:

; (20)

найдем Т, при условии:T=1/ ω,

где Т - период, с.

ω - частота аппроксимированной ЛАЧХ, Гц.

T=1/ ω= 1/0,4=2,5 (с).

График ЛАЧХ пересекает ось Y в точке 18, тогда усиление равно:

20lgk = 18, откуда k=10^18/20=7,94 (21)

С помощью аппроксимации передаточная функция запишется в виде:

(22)

1.4 Моделирование сержня в среде Elcut

Смоделируем нагрев стержня при граничных условиях g₁=0, g₂=10*cos(0,02t). Построим двумерную модель стержня в виде прямоугольника длиной l=3м и высотой h=0,5 м, зададим значения граничных условий на ребрах модели и выберем свойства материала стержня (сталь 20). Решение задачи получим в виде цветовой шкалы, а также графика температуры:

Стержень нагревается от 0 до 0,349 К.

2 Моделирование на макроуровне

2.1 Исходные данные

Дана схема гидравлической системы, представленная на рисунке 4. В системе используется в качестве рабочей жидкости вверенное масло АУ. Материал трубопровода – сталь. Основные параметры системы и жидкости приведены в таблице 1. Параметры трубопровода приведены в таблице 2.

P_B1

P_B2

Qн

P_B3

P_B4

Рисунок 4 – Схема гидравлической системы

1, 2, 3, 4 - магистрали потребителей; P_B1, P_B2, P_B3, P_B4- давление потребителей; Q_H – насос.

Таблица 1 – Параметры системы и жидкости

Обозначение	Основные параметры	Значение
	Плотность рабочей жидкости	860 кг/м^3
	Вязкость	0,15·10^-4 м^2/с
ЕС	Модуль упругости системы	1,7·10^8 Па
Етр	Модуль упругости трубопровода	9·10^10 Па
	Коэффициент потерь на трение при турбулентном потоке	0,028
	Толщина стенки трубопровода	2,2·10^-^3 м

^{Таблица 2 – Параметры трубопровода}

^Параметр	^Обозначение	^Номер трубопровода
		^1	^2	^3	^4	^5
^Диаметр трубопровода	^dтр^, м	^0,015	^0,015	^0,01	^0,01	^0,015
^Длина трубопровода	^l^,м	^1,5	^2	^2	^2	^1
^Коэффициент местных сопротивлений	^ξ	^4,5	^5	^5	^5	^3
^Давление потребителей и насосов	^p^, ×^10^6^Па	^0,1	^0,23	^0,17	^0,15	^-

Q_Н1 = 50×10^-6 м³/с;

Q_Н2 = 300×10^-6 м³/с.

2.2 Графические формы математической модели гидросистемы

2.2.1 Динамическая схема. На основании исходной принципиальной схемы гидравлической системы (рисунок 4) строится динамическая модель. Участки магистралей представляются как последовательное соединение инерционного и диссипативного элемента, причем для инерционного элемента указывается направление движения рабочей жидкости. В точки ветвления магистралей устанавливают упругие элементы, учитывающие сжимаемость жидкости и деформируемость стенок трубопровода. На рисунке 5 представлена полученная динамическая модель.

2.2.2 Орграф. На основании динамической модели построен ориентированный граф, являющийся графической формой модели гидравлической системы. Узлы орграфа соответствуют сосредоточенным массам, а ветви – компонентам математической модели.

Рисунок 5 – Динамическая модель гидравлической системы

Базовый узел (с нулевым номером) отображает инерциальную систему отсчета фазовых координат типа потока. Источник обеспечивает возрастание потоковой переменной узла, поэтому сигналы направляют от базы к узлу. В магистралях потребителей – наоборот. Во всех ветвях инерционных и диссипативных элементов направление сигналов от узла к базе. Такое направление характеризует затраты энергии источников на увеличение кинетической энергии и на трение. В ветвях упругих компонентов стрелки указывают направление передачи энергии от источников к потребителям. В ветвях всех элементов кроме направления записывается параметр каждого элемента. На рисунке 6 представлен полученный орграф.

2.2.3 Матрица инциденций. Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод, для него необходимо сформировать матрицу инциденций, отражающую структуру связей всех элементов системы. Матрица инциденций формируется на основании ориентированного графа. Число строк матрицы соответствует числу узлов орграфа, число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь в ходит в узел – «1», если выходит – «-1».

Рисунок 6 – Ориентированный граф гидравлической системы

Матрицу инциденций А можно представить состоящей из подматриц инерционных А_И, диссипативных А_Д, упругих А_У ветвей и подматрицы ветвей источников потенциалов А_В. Для исходной системы получена матрица, представленная в таблице 3:

А=[A_И, А_Д, А_У, А_В] (23)

Таблица 3 – Матрица инциденций гидравлической системы

Узлы	Ветви
	Диссипативные					Упругие	Источники потенциалов
№	μ1	μ 2	μ3	μ 4	μ 5	С1	Рв1	Рв2	Рв3	Рв4	Q5
1	-1	0	0	0	0	1	-1	0	0	0	0
2	0	-1	0	0	0	1	0	-1	0	0	0
3	0	0	-1	0	0	1	0	0	-1	0	0
4	0	0	0	-1	0	1	0	0	0	-1	0
5	0	0	0	0	-1	-1	0	0	0	0	1
Подматрица	АД					АУ	АВ

2.3 Узловой метод формирования математической модели гидросистемы

Из матрицы инциденций можно получить систему равнений (24), математически описывающие функционирование гидравлической системы:

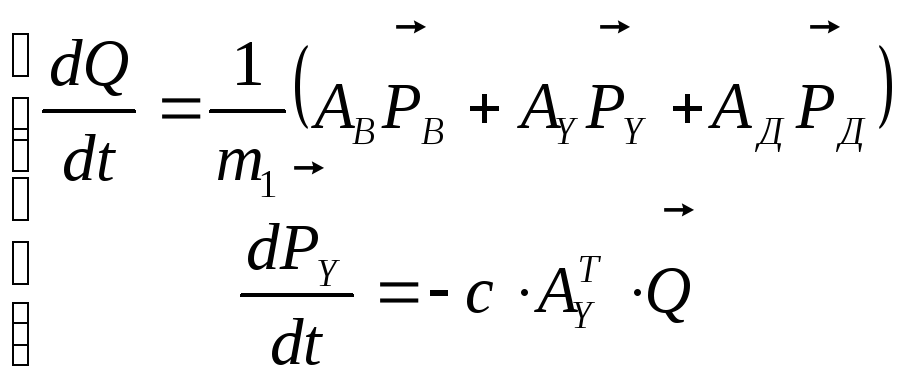(24)

где ;

А_Д, А_У, А_В – подматрицы инциденций;

- векторы давлений;

- векторы расходов,

m, с, μ - диагональные матрицы параметров элементов гидравлической системы.

Для нашего случая система будет иметь вид:

(25)

Так как в исходной системе насос постоянной производительности, то = 0 и пятое уравнение (25) преобразуется к виду:

P_H = P_Д5 + P_У1 (26)

С учетом возможного турбулентного режима течения рабочей жидкости, а так же возможных местных потерь, связанных с изгибом трубопровода, зависимость для диссипативных элементов будет носить более сложный характер:

(27)

где μ_л - коэффициент гидравлического сопротивления, характеризующий

линейные потери при ламинарном режиме движения жидкости;

μ_н - коэффициент гидравлического сопротивления, характеризующий нелинейные потери при турбулентном режиме, по длине и местные.

Таким образом, математическая модель рассматриваемой гидросистемы представляется системой пяти дифференциальных уравнений и шестью алгебраическими выражениями.

Вычисление параметров трубопровода гидросистемы

Значения коэффициентов линейных и нелинейных потерь для конкретной магистрали находят по формулам:

- площадь сечения трубопровода, м²:

; (28)

- коэффициент линейных потерь, H·с/м⁵;

; (29)

- коэффициент нелинейных потерь, H·с/м⁵.

; (30)

- коэффициент жесткости участка:

; (31)

где Ψ - доля объема трубопровода;

V_тр - объем трубопровода, м³:

V_тр=S_тр·l . (32)

Доля объема трубопровода рассчитывается как отношение объема отдельного участка к сумме объемов всех n соединенных между собой участков:

(32)

где - объем трубопровода i-ого участка, м³.

Коэффициент жесткости упругого элемента:

. (34)

По исходным данным и полученным результатам находим жесткость упругого элемента c₁= 6,755·10¹¹ Н/м⁵.

Коэффициент массы:

. (35)

Полученные результаты для отдельных участков трубопровода приведены в таблице 4.

Таблица 4 – Параметры трубопровода гидросистемы

Параметр	Номер магистрали
	1	2	3	4	5
Площадь сечения трубопровода, Sтр, ×10^-4м^2	1,767	1,767	0,785	0,785	1,767
Объем трубопровода, Vтр, ×10^-4м^3	2,651	3,534	1,571	1,571	1,767
Доля объема трубопровода,	0,239	0,319	0,142	0,142	0,159
Коэффициент массы, mг, ×10^6кг/м^4	7,3	9,733	21,9	21,9	4,867
Коэффициент линейных потерь,, ×10^7H·с/м^5	1,561	2,082	10,54	10,54	1,041
Коэффициент нелинейных потерь,, ×10^11H·с/м^5	1,005	1,202	7,388	7,388	0,670
Коэффициент жесткости участка, cг, ×10^12Н/м^5	2,649	1,490	7,576	7,576	5,960

2.4 Расчёт статической модели гидросистемы

При постоянном воздействии система находится в установившемся равновесном состоянии. Ее фазовая координата (давление Р и расход Q) при этом постоянна. Такой режим функционирования системы называется статическим и достигается при постоянном внешнем воздействии:

– давления к потребителю (Р_В1, P_В2, P_В3, P_В4),

– подачи насоса Q_H.

При этом устанавливаются постоянные значения фазовых координат системы:

– расход в гидромагистралях,

– давление в упругом элементе.

Из данного утверждения следует:

(36)

Из (24) и (26) получаем систему для статического режима:

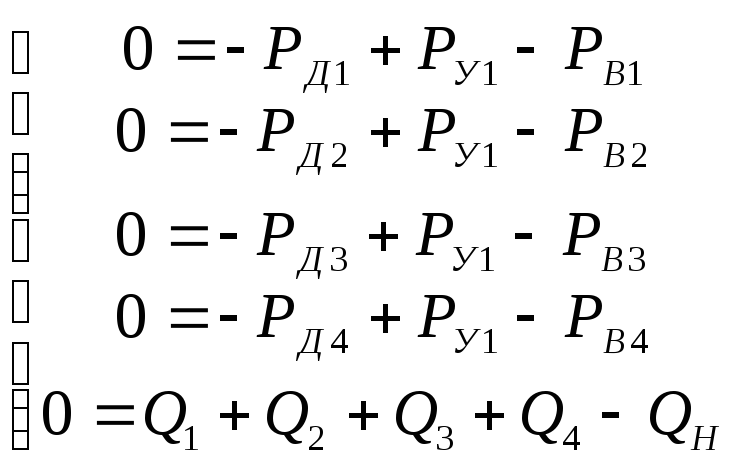(37)

Учитывая нелинейные свойства диссипативных элементов гидравлической системы, их компонентное уравнение имеет вид:

(38)

Перенесем в правую часть системы внешние воздействия, тогда статическая модель будет иметь вид:

(39)

Для ее решения используются численный метод, для которого предварительно сформируем матрицу Якоби. Элементами матрицы Якоби для сформированной нелинейной системы являются частные производные от нелинейной вектор-функции по фазовым координатам системы (Q₁, Q₂, Q₃, Q₄, P_У1).

(40)

Нахождение частной производной по расходу от давления в диссипативном элементе (38) имеет вид:

(41)

Матрица Якоби исходной гидросистемы имеет вид:

(42)

тогда матрица (42) принимает вид:

Для решения статической модели используем численный метод Ньютона, алгоритм которого включает следующие этапы:

– выбор начального приближения , где - вектор фазовых координат (Q₁, Q₂, Q₃, Q₄, P_У1), V₀ – нулевой вектор-столбец;

– вычисление матрицы Якоби J_k в точке _K (k=0, 1, 2 …);

– вычисление вектора невязок . Вектор невязок получается из системы уравнений (27) для статического режима:

(43)

– определение вектора поправок:

. (44)

– определение нового приближения вектора искомых фазовых переменных:

. (45)

– проверка условия окончания итерационного процесса, при выполнении условия, что V_k и V_k+1 соизмеримы (совпадают до десятых), иначе происходит переход на предыдущие этапы и вычисляется следующая итерация.

Расчет фазовых координат при статическом процессе произведен в математическом пакете MathCad.

При Q_H = 100×10^-6 м³/с решением является матрица:

(46)

При Q_H = 300*10^-6 м³/с решением является матрица:

(47)

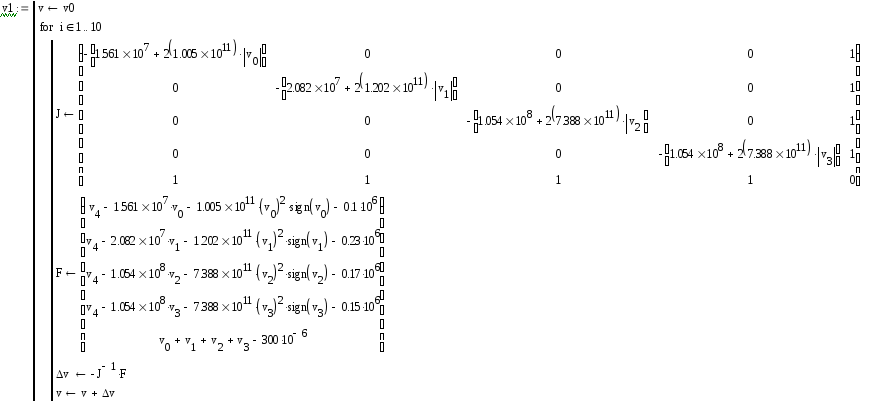
Результаты вычислений приведены в таблице 5.

Таблица 5 – Результаты статического анализа

Фазовая координата	при Qн=100×10^-6, м^3/с	при Qн=300×10^-6, м^3/с
Q1, м^3/с	7,228×10^-4	7,745×10^-4
Q2, м^3/с	-6,607×10^-4	-6,111×10^-4
Q3, м^3/с	-4,487×10^-5	1,984×10^-5
Q4, м^3/с	8,276×10^-5	1,168×10^-4
Pу1, Па	1,638×10^5	1,724×10^5