2.5 Анализ динамической модели гидросистемы

Динамическая модель описывает переходный процесс гидросистемы. В общем случае система дифференциальных уравнений, описывающих гидравлическую систему, имеет вид:

(48)

где А – матрица Якоби,

- вектор фазовых координат,

- вектор функции внешних воздействий.

С учетом произведенных ранее расчетов, запишем систему дифференциальных уравнений, представляющую динамическую гидросистему:

(49)

Для динамической модели матрицу Якоби можно записать аналогично статической модели:

(50)

Переходный процесс определяется в результате численного интегрирования системы (49), для чего необходимо произвести выбор ряда параметров.

Пусть переходный процесс оценивается как реакция системы, находящейся в состоянии покоя, на ступенчатое воздействие вида:

(51)

где u₀ и u_k – начальное и конечное значение функции воздействия u(t), причем u₀ и u_k – константы, (u₀ ≠ u_k):

(52)

Начальные (46) и конечные (47) значения всех фазовых координат определены при анализе статического режима (таблица 5).

=> (53)

Если система устойчивая, то через некоторый промежуток времени, система перейдет из состояния V₀ в состояние V_k. Для численного интегрирования будем использовать неявный метод Эйлера. Вектор входных воздействий V_k при имеет вид:

(54)

2.5.1 Выбор шага интегрирования. Для устойчивости самого метода проведем выбор шага интегрирования h исходя из условия:

, (55)

где - собственное значение матрицы Якоби.

Для комплексного значения условие имеет вид:

(56)

Собственными значениями матрицы Якоби порядка n называют корни , где , ее характеристического уравнения, определяемого по формуле:

(57)

где А – матрица Якоби динамической модели;

Е – единичная матрица.

Произведем расчет матрицы Якоби по формуле (50), подставляя начальные значения фазовых координат:

(58)

Тогда характеристическое уравнение имеет вид:

(59)

Вычислим корни характеристического уравнения с помощью программы MathCad, тогда собственные значения матрицы Якоби имеют вид:

(60)

Корни характеристического уравнения имеют как отрицательные, так и положительные значения действительных частей, что говорит о неустойчивости системы.

Наличие комплексно-сопряженных корней дает затухающий колебательный процесс ряда фазовых координат. Для гидравлической системы рекомендуемый шаг интегрирования h = 0,5с. Выполним проверку устойчивости численного метода Эйлера при данном шаге.

При λ = 0: |1 - h·λ| = 1;

При λ = -0,971: |1 - h·λ| = 1,486

При λ = 0,0671 + 0,694i:

(Re(h·λ) – 1)² + (Im(h·λ))² = 0,93 + 0,12 = 1,054

При λ = 0,0671 - 0,694i:

(Re(h·λ) – 1)² + (Im(h·λ))² = 0,93 + 0,12 = 1,054

Проверка условий выполняется, следовательно, шаг h = 0,5 обеспечит устойчивость метода и приемлемую точность вычислений.

2.5.2 Решение систем дифференциальных уравнений методом Эйлера. Формула численного интегрирования неявного метода Эйлера имеет вид:

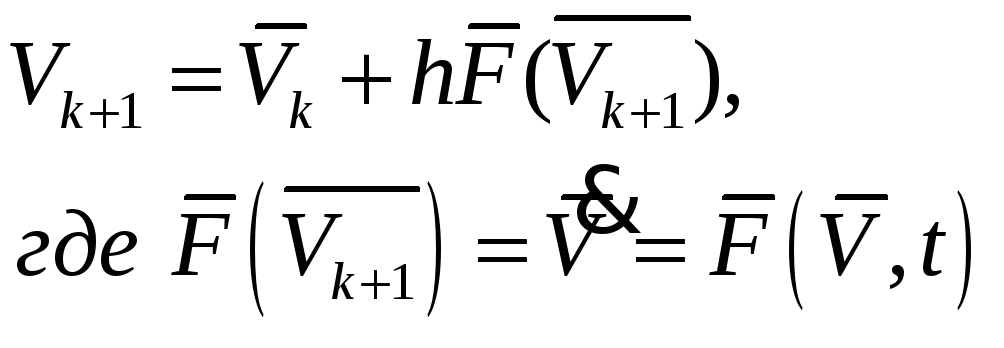(61)

Совместное преобразование двух последних выражений приводит к записи:

(62)

где - модифицированная матрица Якоби на k+1 шаге, которая формируется по следующему правилу: диагональные элементы матрицы Якоби на k-ом шаге пересчитываются по формуле:

(63)

Остальные элементы не изменяются. Для матрицы размерности 5х5 получаем:

(64)

- модифицированный вектор входных воздействий на k+1 шаге, определяемый по формуле:

(65)

Решение системы уравнений (61) дает значение фазовых координат на k+1 шаге, то есть в момент времени t_k+1.

Алгоритм неявного метода Эйлера с постоянным шагом интегрирования h:

1. задание шага интегрирования h;

2. задание начальных значений фазовых переменных при t₀=0;

3. вычисление времени t_k+1=t_k+h, где k=0,1,2…;

4. вычисление модифицированных матриц и на k+1 шаге;

5. решение системы уравнений (61) с целью определения в момент времени t_k+1;

6. переход к этапу (3) до тех пор, пока в случае устойчивой системы фазовые координаты не достигнут состояния конечного значения .

Начальные значения вектора определяются на основании входных воздействий системы. В качестве начальных значений фазовых переменных берем вектор начальных значений .

Рисунок 7 – Графики фазовых координат f(n)₀, f(n)₁, f(n)₂, f(n)₃

Рисунок 7 – Переходный процесс гидросистемы