Составление матрицы планирования.

Проведем оптимизацию полного факторного эксперимента. Для полного факторного эксперимента, в котором реализуются все возможные сочетания уровней факторов, число опытов определяется по следующей формуле: N = 2^k. Будем рассматривать задачу с максимальным числом факторов равным трем и числом опытов 2³=8.

На основании заданных данных построим матрицу планирования.

Первоначально введем условное обозначение верхнего(+) и нижнего(-) уровня.

Таблица №3

№	х1	х2	х3			S
1	-	-	-	0.11	0.0001	0.01	0,117	0,000049
2	+	-	-	0.12	0.0072	0.085	0,105	0.000225
3	-	+	-	0.203	0.00003	0.006	0,201	0,000004
4	+	+	-	0.177	0.00003	0.006	0.189	0,000144
5	-	-	+	0.12	0.0004	0.02	0.125	0,000025
6	+	-	+	0.11	0.0001	0.01	0.113	0,000009
7	-	+	+	0.217	0.00023	0.015	0.209	0,000064
8	+	+	+	0.197	0.00023	0.015	0.197	0

1. Подсчитываем средние значения в сериях каждого опыта.

(1)

где у_i – i-ое значение в серии опытов; n – количество опытов в серии.

2. Подсчитываем дисперсию S² различных серий опытов.

(2)

3. Квадратичная ошибка или стандарт:

. (3)

Проверяем вторую серию опытов (с максимальным значением дисперсии S²=0.0072) на наличие ошибки с помощью критерия Стьюдента: ,

где t – табличное значение критерия Стьюдента.

Коэффициент Стьюдента для степени свободы (n – 1)=(3 – 1)=2 равен t=4.3.

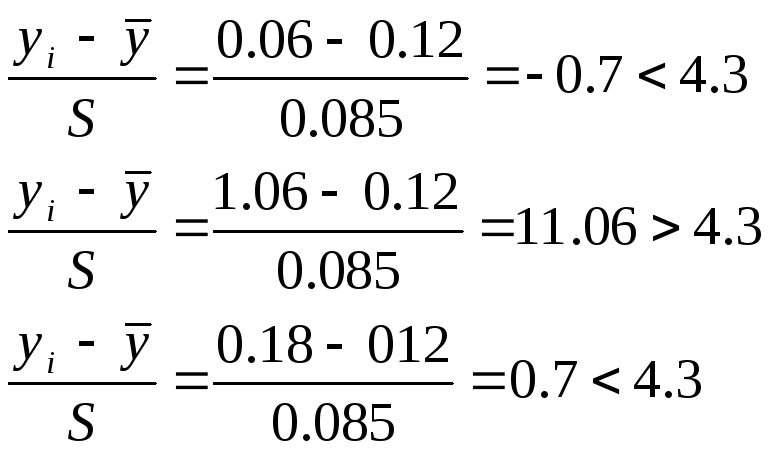
А значит значение опыта равное 1.06 – промах и из дальнейшего рассмотрения мы его исключаем.

Проверяем дисперсию на однородность.

(4)

Полученное значение больше табличного значения критерия Фишера равного F=18.5 для степеней свободы числителя f₁=n–1=2-1=1 и знаменателя f₂=n–1=3-1=2, значит дисперсия неоднородная.

Находим дисперсию выходного параметра.

, (5)

РАСЧЕТ ЛИНЕЙНОЙ МОДЕЛИ

у=b₀+b₁х₁+b₂х₂+ b₃х₃ (6)

Рассчитаем коэффициенты для линейной модели (b₀,b_1,b_2,b₃)

по формуле: b_i= (7)

Получим следующие коэффициенты:

b₀=

b₁=

b₂=

b₃=

Тогда линейная модель запишется в виде:

у=0,157-0,006х₁ +0,042х₂+0,004х₃ (9)

Определяем по этой модели расчетные значения параметра оптимизации

= f(x) и заносим эти значения в таблицу.

После чего находим квадрат отклонения экспериментального значения от расчетного: (10)

Заносим полученные значения в таблицу.

После построения модели необходимо провести проверку ее адекватности.

ОЦЕНКА АДЕКВАТНОСТИ МОДЕЛИ.

Найдём дисперсию адекватности по следующей формуле:

(11)

где f = N – (n + 1) =8-(3+1)=4

Проверяем модель на адекватность, для чего находим расчетный коэффициент Фишера как отношение:

(12)

Полученное значение сравниваем с табличным значением критерия Фишера F=19,3 для f₁=4 и f₂=2 и поскольку полученное значение не превышает его, то полученная линейная модель адекватна.