курсовая работа / курсовой / 1часть

ВВЕДЕНИЕ

Под моделированием понимается процесс замещения реального объекта некоторой моделью, позволяющей проводить над ней определенные исследования. В зависимости от уровня абстрагирования выделяют три иерархических уровня: микро-, макро- и мегауровень. Цель курсовой работы — моделирование некоторых физических процессов на микро- макроуровне.

Под моделированием на микроуровне понимается также теория систем с распределенными параметрами. Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.). Система с распределенными параметрами (СРП) – это система, в которой практически все сигналы зависят от пространственных координат и времени. Математически СРП описываются дифференциальными уравнениями в частных производных с начальными и граничными условиями, составляющие краевую задачу. Для ее решения в статике и динамике используется функция Грина, являющаяся решением краевой задачи при входном воздействии в виде дельта-функции и нулевых начальных и граничных условиях, а также континуальная передаточная функция, являющаяся преобразованной по Лапласу функцией Грина. В данной работе, при моделировании на микроуровне решается вопрос построения математической модели мембраны, жестко закрепленной по краям.

На макроуровне исследуется гидравлическая система. При разработке и исследовании модели макроуровня необходимо выполнить: синтез моделей в графической и матричный формах, в виде системы обыкновенных дифференциальных уравнениях, а также анализ полученной математической модели в статическом и динамическом режиме.

1 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ

1.1 Выбор уравнения и его идентификация

Уравнения математической физики являются основой для построения математической модели элементов и систем управления с распределенными параметрами. Для их практического применения основной сложностью является выбор уравнения, которое могло бы заданной точностью и степенью достоверности описать интересующий элемент системы.

Рассмотрим процесс колебания струны под действием на нее давления.

Колебательные процессы описываются уравнениями гиперболического типа. Рассмотрим одномерную задачу: распространение колебаний по струне.

Выберем дифференциальное уравнение:

(1)

Начальные условия:

Q(x,0)=Q₀(x)= 0.01*sin(15x+2.5) ,

(2)

Граничные условия ( с учетом, что один конец струны жестко закреплен):

; (3)

0≤x≤l, t≥0, a≠0, l=0.3м – длина струны.

Входное воздействие:

f(x,t)= 45000*sin(0.2*t)+45000 (4)

Коэффициент а представляет собой отношение поверхностного натяжения Т[Н/м]к плотности струны и имеет размерность а=[м/с].

В данной работе принимаем а=1 м/с. Принимаем [1/с].

Стандартизирующая функция:

, (5)

где Q0(t) – начальная функция, описывающая искомую функцию Q в начальный

момент времени,

Q(t) – производная от Q(t), [м]

g(t) – граничные условия, [м/с]

(t) – импульсная переменная функция, [с]

^/(t) – производная от (t) – функции по времени.

Функция Грина:

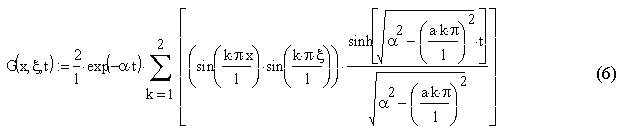
Континуальная передаточная функция:

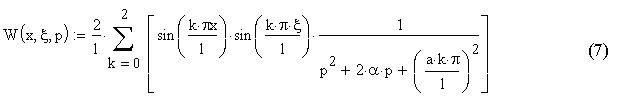
1.2 Расчет статической характеристики. Расчет функции распределения.

Зная стандартизирующую функцию и функцию Грина можно найти выходную функцию, вычислением интеграла, представляющий собой основное соотношение, связывающее выход объекта при заданном начальном состоянии с выходными воздействиями:

(8)

Для этого вычислим составляющие Q(x,t) по формуле:

Q(x,t)=Q₁(x,t)+Q₂₁(x,t)+ Q₂₂(x,t)+Q₃(x,t) , (9)

где

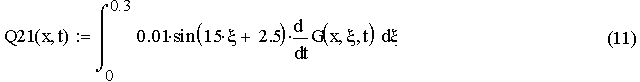
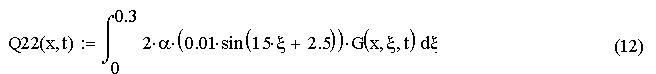
Получим:

(x,t)=Q₁(x,t)+Q₂₁(x,t)+ Q₂₂(x,t)+Q₃(x,t)

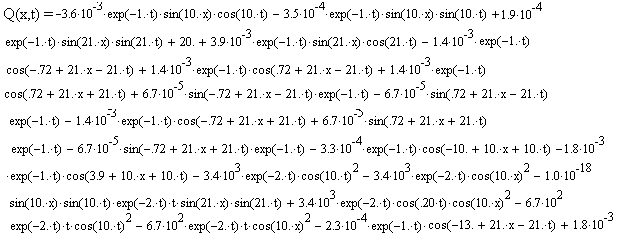
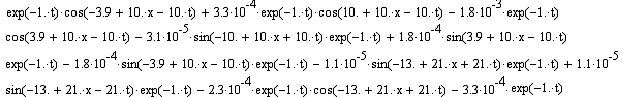
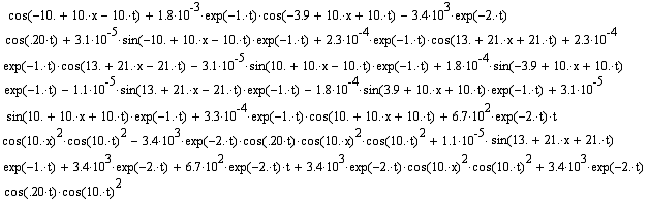
Построим функцию отклонения струны для t=0.1 с. :

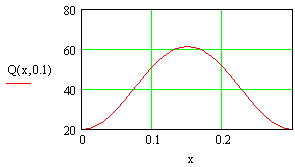
Рисунок 1 – Отклонение струны для t=0.1 с.

1.3 Расчет динамической характеристики.

Расчет интегральной передаточной функции. Преобразование Лапласа от интегральной передаточной функции. Построение переходного процесса и частотных характеристик. Получение передаточной функции.

По заданному дифференциальному уравнению объекта получим выражение для передаточной функции в распределенных параметрах. Построим ЛАЧХ, аппроксимируем ее с погрешностью 5% , запишем выражение передаточной функции через типовые звенья.

Для расчета необходимо найти преобразование по Лапласу стандартизирующей функции, которая имеет вид:

(14)

Преобразуя данное выражение, получим:

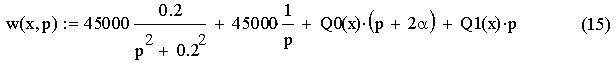
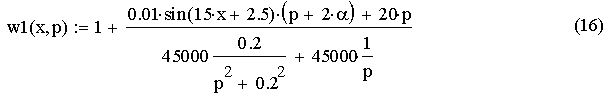
Заменим х →ξ и упростим:

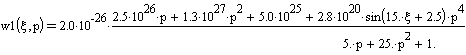
Континуальная передаточная функция имеет вид:

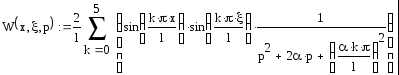(17)

Вычислим интегральную передаточную функцию:

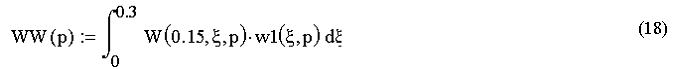
Получим:

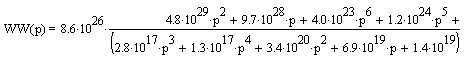
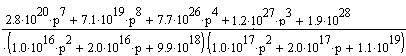
В выражении для интегральной передаточной функции сделаем замену

Получим:

1.4 Построение ЛАЧХ и нахождение аппроксимированной передаточной функции

По полученной передаточной функции построим ЛАЧХ. Найдем выражение для логарифмической амплитудно-частотной характеристики:

(19)

Аппроксимируя ЛАЧХ стандартными наклонами получим 0 дб/дек,

-20 дб/дек, и -60дб/дек. Такие наклоны соответствуют инерционному и апериодическому звеньям. Запишем передаточную функцию

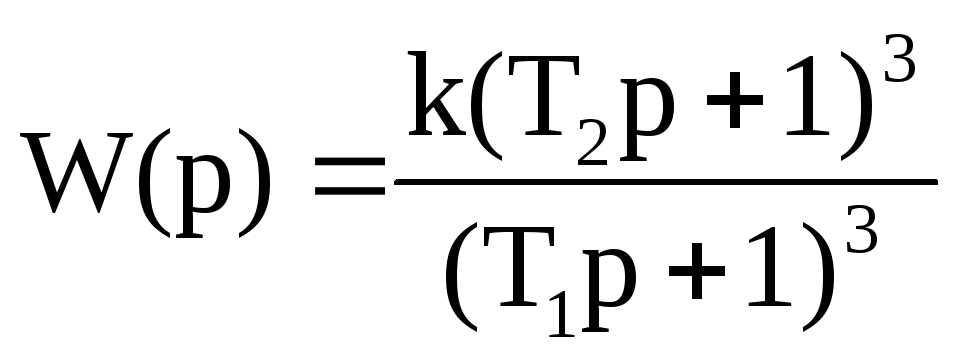
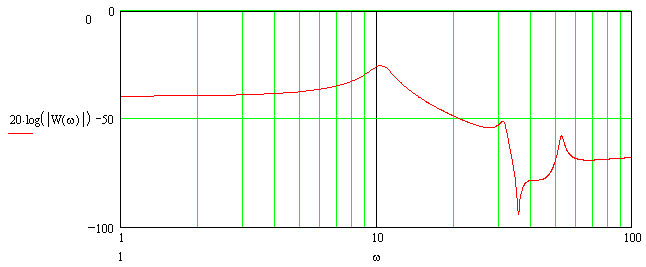
Рисунок 4 – График логарифмической амплитудно-частотной характеристики.

					УИТС.423311.210 ПЗ	Лист
						39
Изм	Лист	№ докум	Подп.	Дата.