4. Тройной интеграл

Пусть непрерывная функция определена в замкнутой, ограниченной области (Т)  R³. Разобьем (Т) на частичные подобласти (Т_к), 1 k  n, обозначим через d_k диаметр (Т_k): через V_k – объем (Т_k). В каждой частичной области (Т_к) выберем по точке M_к(x_k;y_k;z_k). Выражение

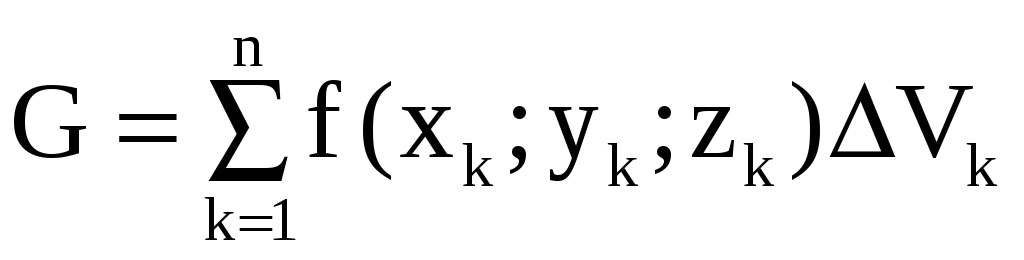
называется интегральной суммой функции f(x;y;z) по области (Т). Число называется диаметром разбиения. Если существует предел интегральных сумм при (предел, не зависящий ни от способа разбиения (Т), ни от выбора точек M_к), то этот предел называется тройным интегралом функции u = f(x;y;z) по области (Т) и обозначается

Свойства тройного интеграла аналогичны свойствам двойного интеграла. Вычисление тройного интеграла сводится к вычислению повторного интеграла. Если область (Т) ограничена снизу поверхностью z = ₁(x;y), сверху – поверхностью z = ₂(x;y), с боков – цилиндрической поверхностью с образующей, параллельной оси 0z, и (D) – проекция тела (Т) на координатную плоскость 0xy, то

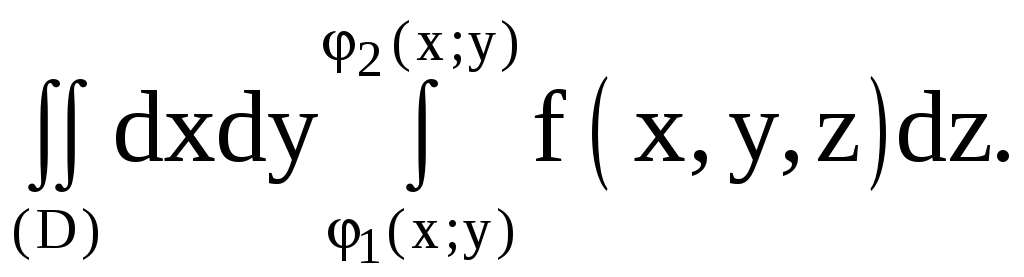
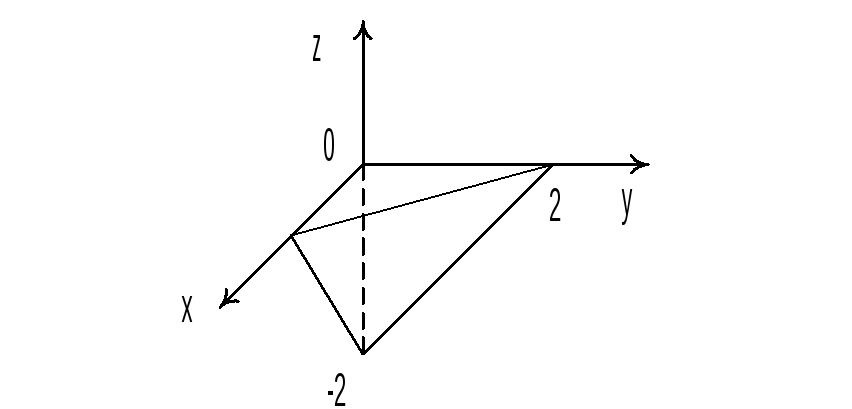
Пример 9. Вычислить где область (T) ограничена поверхностями 2x + y –z = 2, x = 0, y = 0, z = 0.

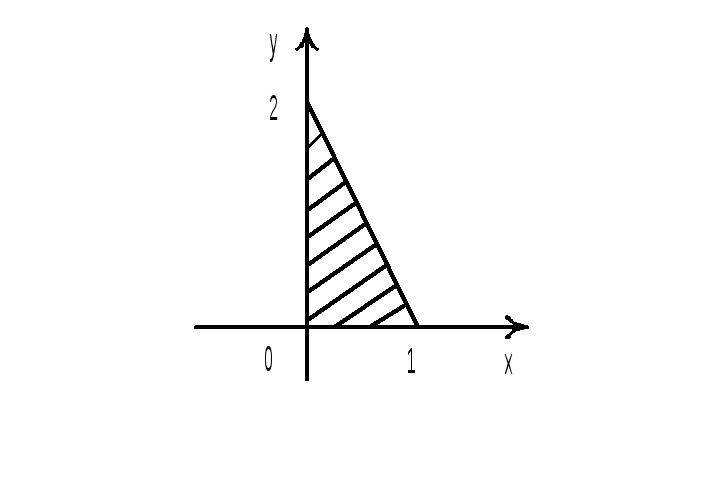
Решение. Поверхности, ограничивающие нашу область, являются плоскостями, и (Т) является тетраэдром. Сведем тройной интеграл к повторному. Область (T) задаётся системой неравенств Чтобы найти проекцию (D) области (T) на координатную плоскость 0xy решим систему 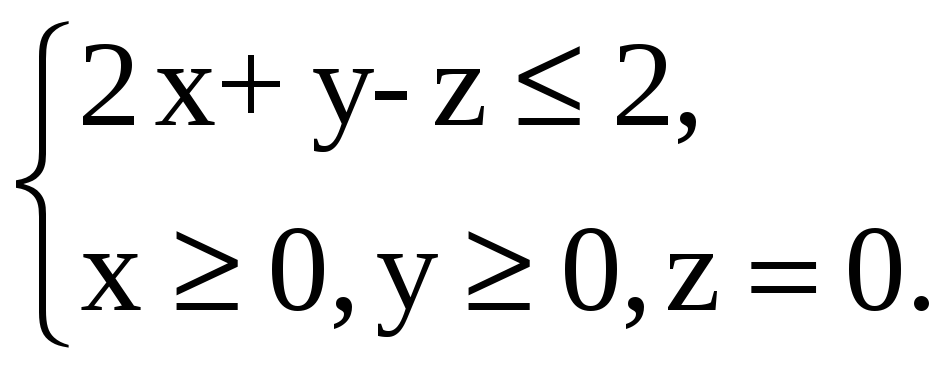Следовательно проекцией (D) области (T) на координатную плоскость 0xy является прямоугольный треугольник, определяемый неравенствами 2x + y  2, x  0, y  0. Поэтому границы изменений переменных x, y, z задаются неравенствами

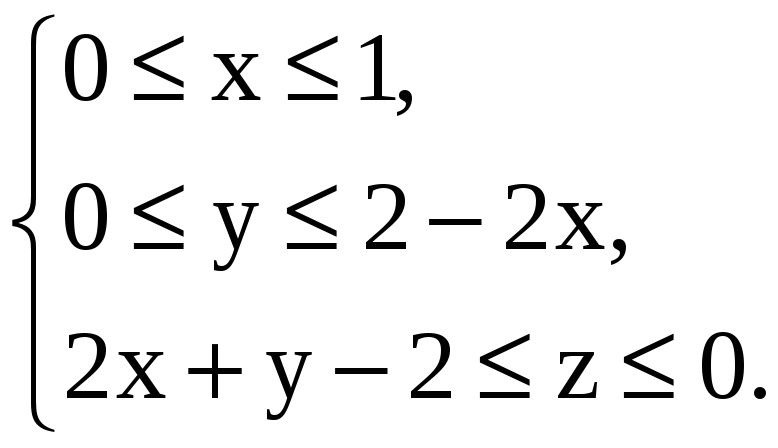
Таким образом,

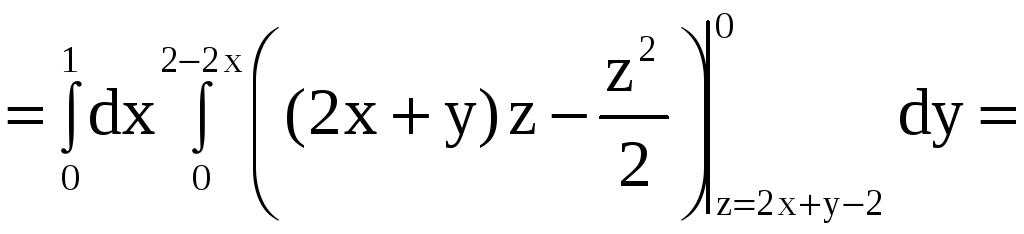
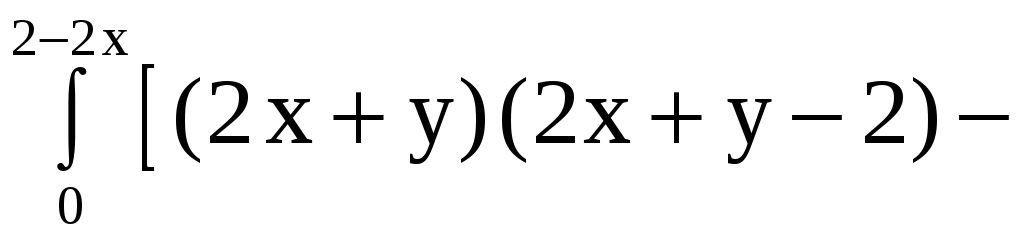
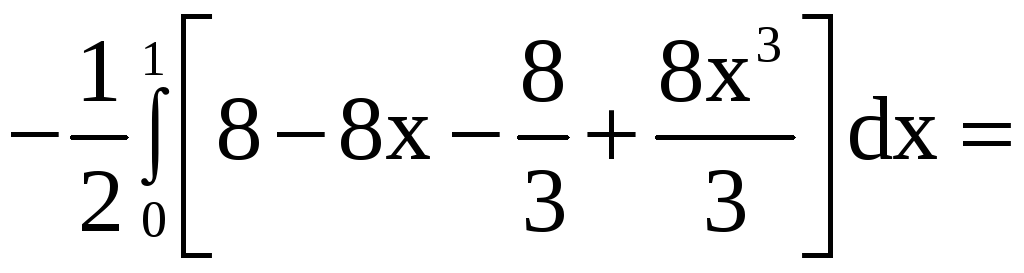
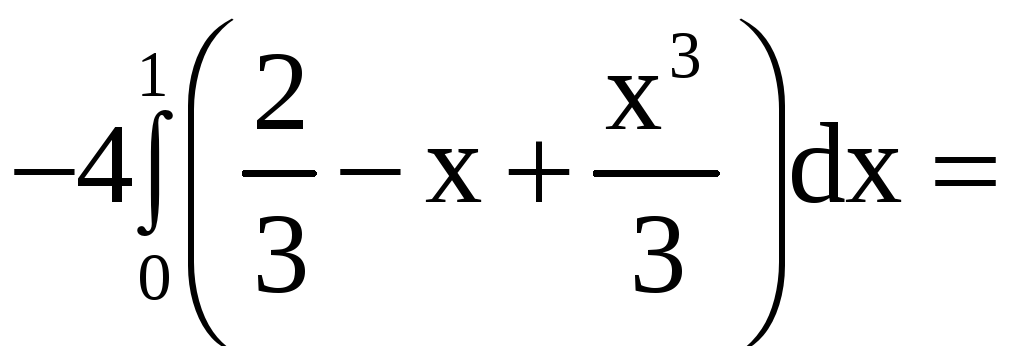
5. Замена переменных в тройном интеграле

Тройной интеграл иногда проще вычислить, если перейти к новой системе координат 0uvw.

Е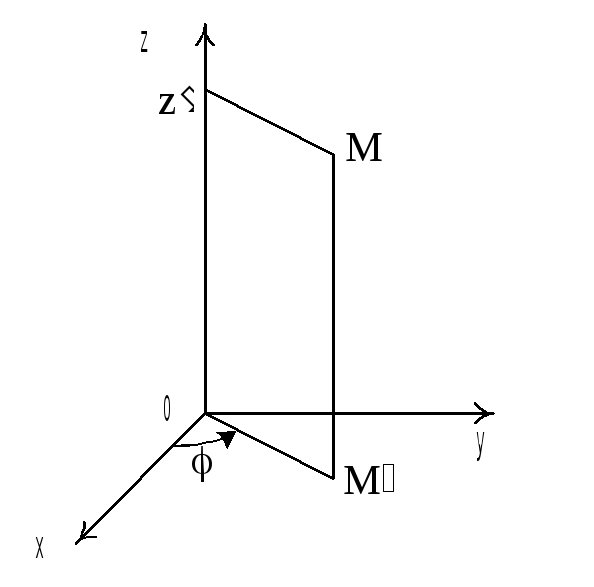сли замена переменных происходит с помощью функций , , и эти функции осуществляют взаимно − однозначное соответствие между областью (Т) в системе 0xyz и областью (Т₁) в системе 0₁uvw и якобиан 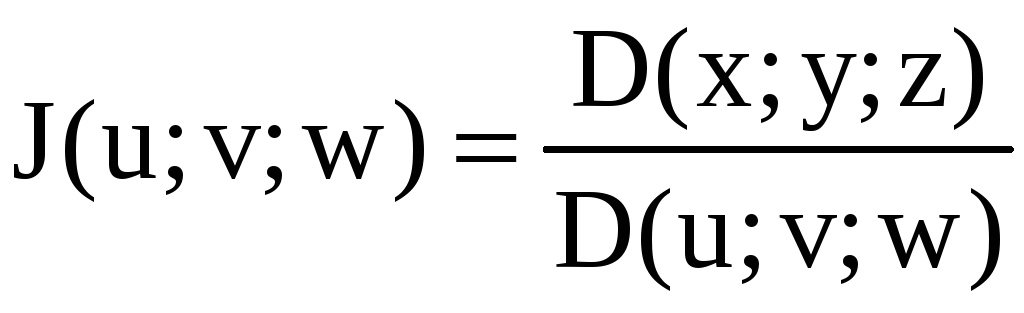непрерывен и не обращается в нуль, то справедлива формула

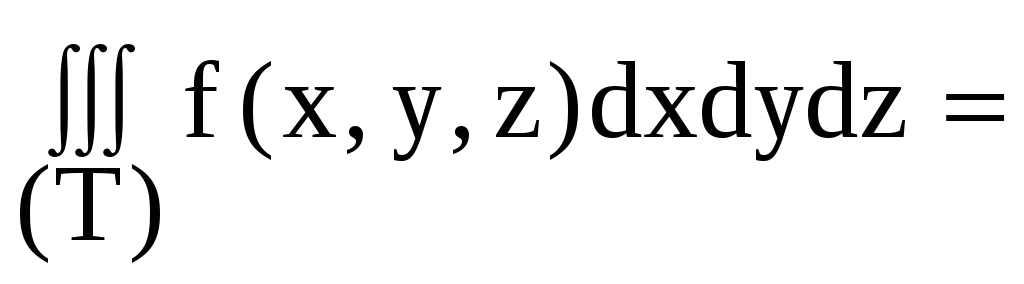
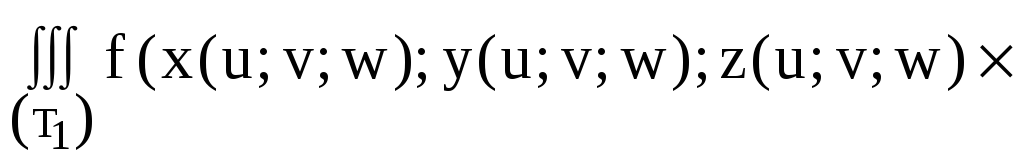
. (9)

Наиболее употребительными из криволинейных координат являются цилиндрические и сферические системы координат.

В цилиндрической системе координат каждой точке М пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел – длина отрезка , где М – проекция точки М на плоскость 0xy,  – угол между вектором и положительным направлением оси 0x, z совпадает с третьей координатой точки М в декартовой прямоугольной системе координат (числа  и  являются полярными координатами точки М в системе 0xy). Переменные , , z могут принимать значения: , 0   <  (или

–   < ), – < z < +. Уравнение  = с, где с – константа, с  0, задает цилиндр в пространстве, уравнение  = с задает полуплоскость, z = c – плоскость. Переход к цилиндрической системе координат осуществляется с помощью формул

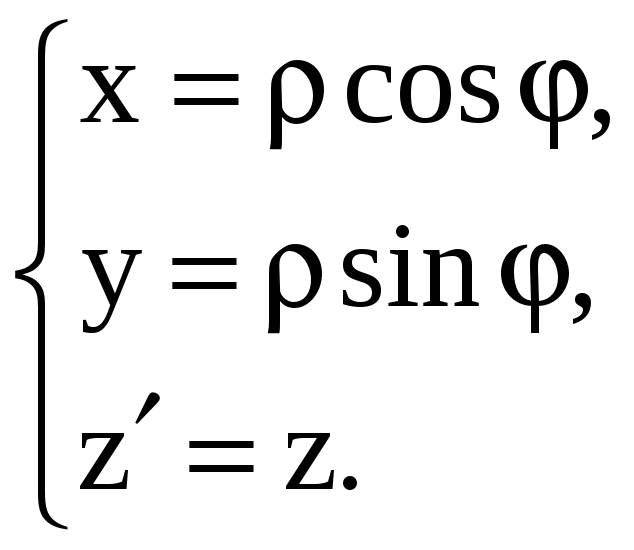
Якобиан перехода равен J = . При этом формула (9) принимает вид

(9)

(Часто вместо z пишут просто z).

В сферической системе координат каждой точке М(x;y;z) пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел (, , ) – сферические координаты, где  – длина вектора  – угол между вектором и положительным направлением оси 0z, – угол между вектором и положительным направлением оси 0x (М, как и выше, – проекция точки М на плоскость 0xy). Переменные , ,  могут принимать следующие значения:   0, 0    , 0   < 2 (или –   < ).

У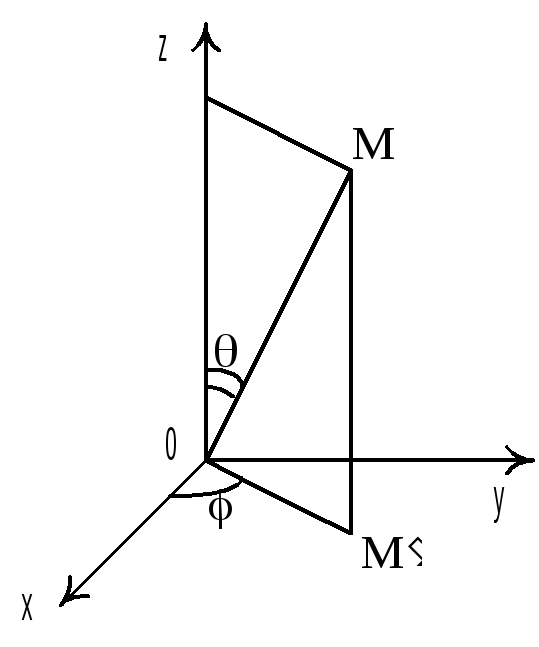равнение  = c, c  0 задает сферу радиуса c (чем и объясняется название системы координат), – однополостный круговой конус,  = c – полуплоскость.

Формулы перехода к сферической системе координат имеют вид

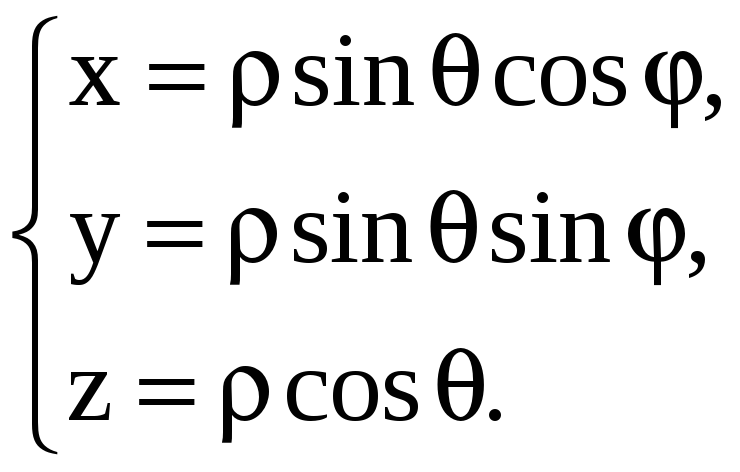
Якобиан перехода J = ²sin. Формула (9) примет вид

(9)

Наряду с приведенной только что сферической системой координат (назовем ее сферической системой координат первого типа) употребляют

с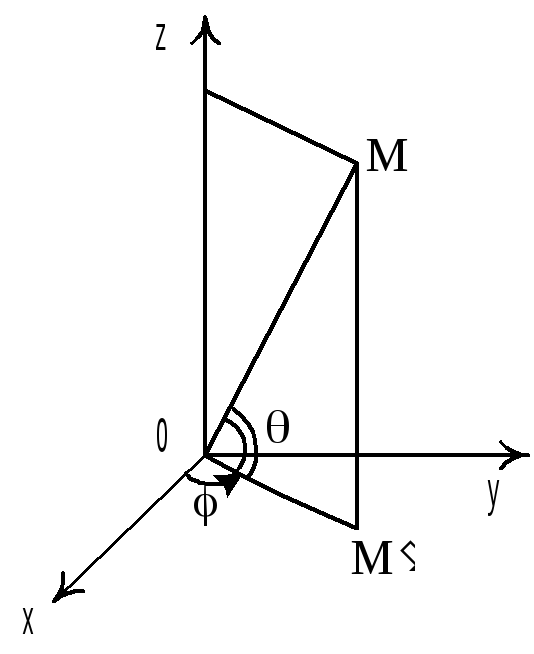ферическую систему координат второго типа. Она отличается от системы первого типа только способом определения второй координаты : в сферической системе координат второго типа  есть угол между вектором и плоскостью 0xy; при этом  может меняться в пределах отрезка 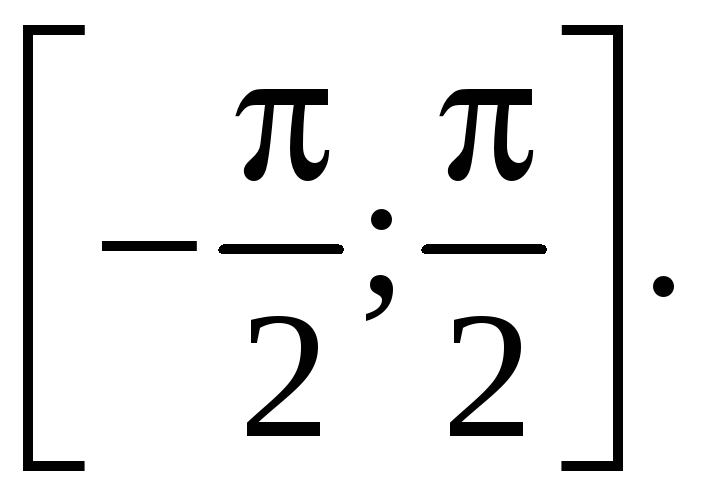Формулы перехода к такой системе координат имеют вид

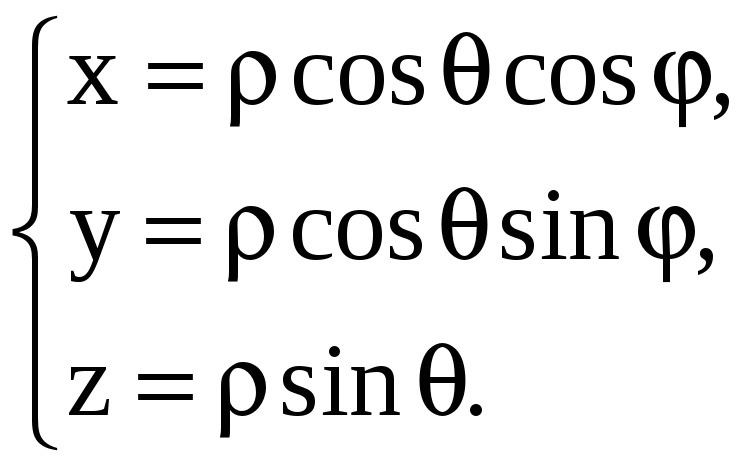
Якобиан преобразования J = ²cos.

При переходе к такой сферической системе формула (9) примет вид

. (9)

Пример 10. Перейдя к цилиндрическим координатам, вычислите 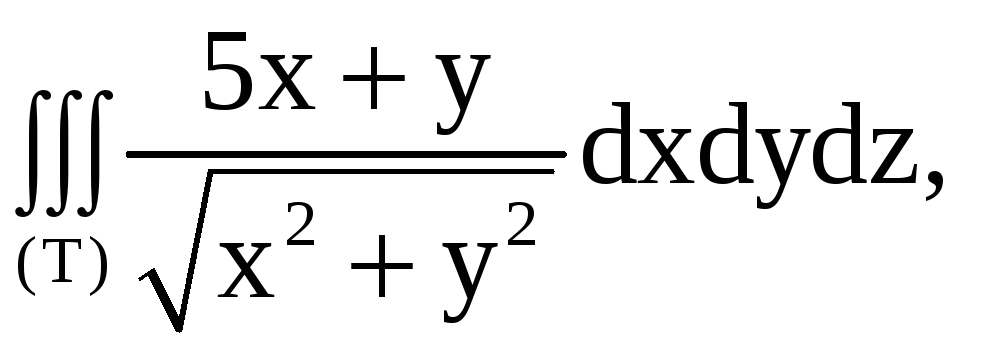где (Т) ограничено поверхностями

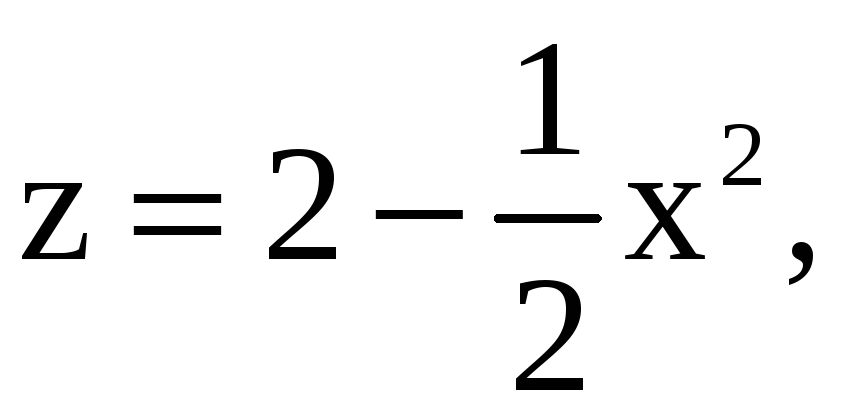
Р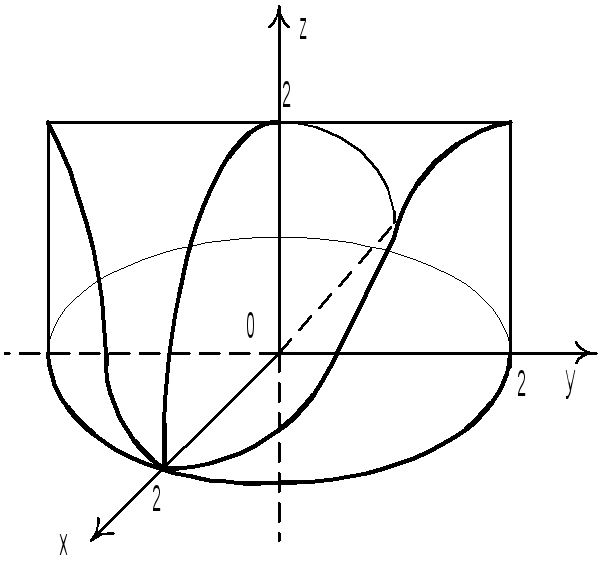ешение. Уравнение  задает параболический цилиндр с образующими, параллельными оси 0y, задает цилиндр. Область, на которую распространяется интеграл, изображена на рисунке. Проекцией (Т) на плоскость 0xy является круг радиусом 2 с центром в начале координат; перейдем к цилиндрической системе координат:

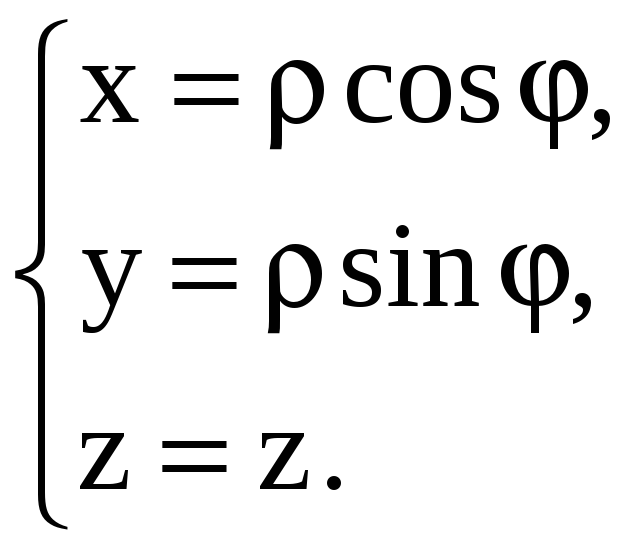
Тогда J = , 0    2, 0   < 2, 0  z 

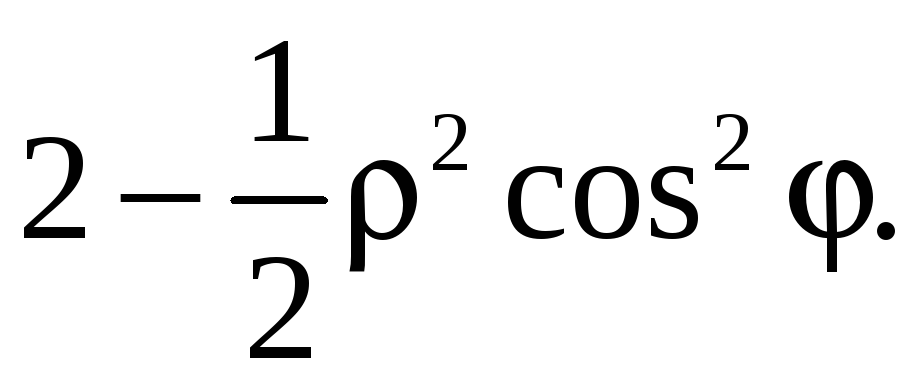
Применив формулу (9), получим

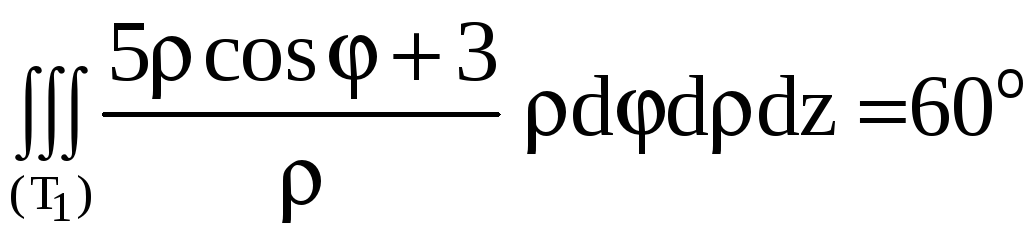
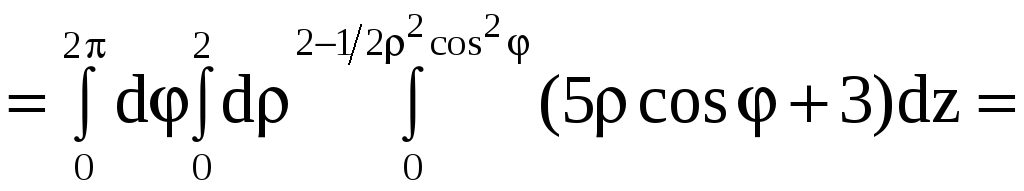
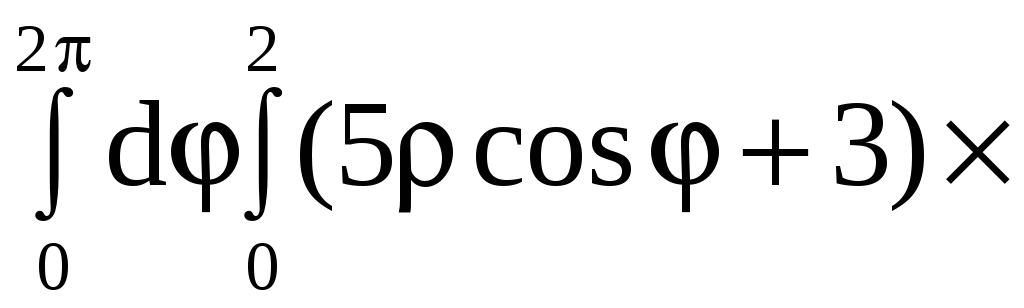
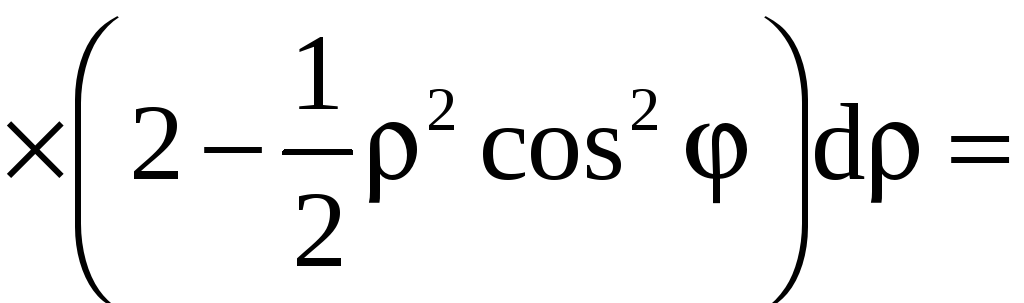
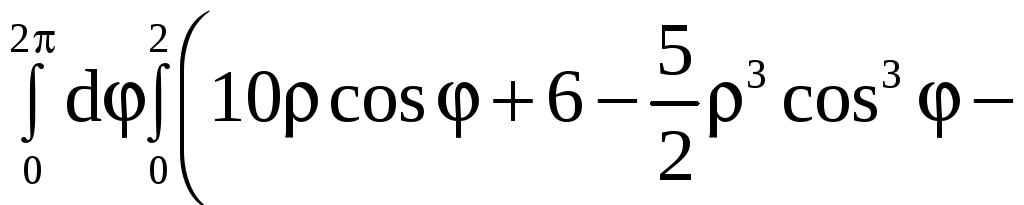
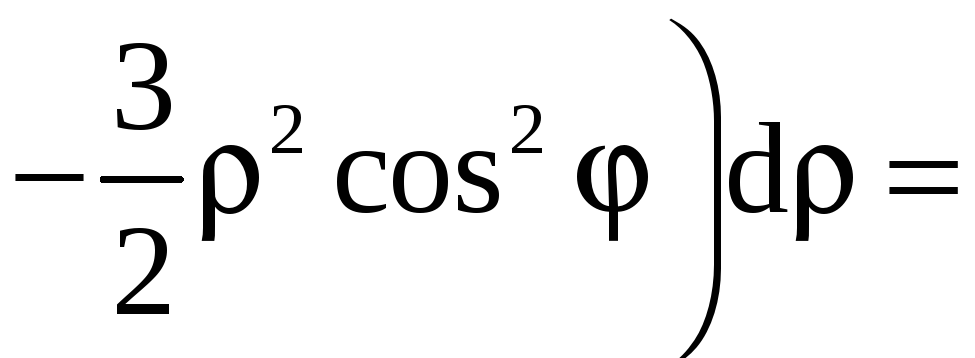
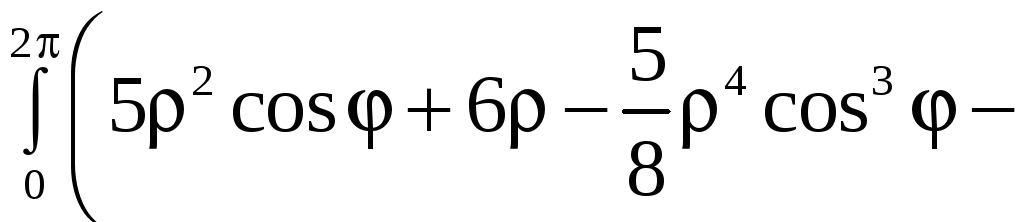
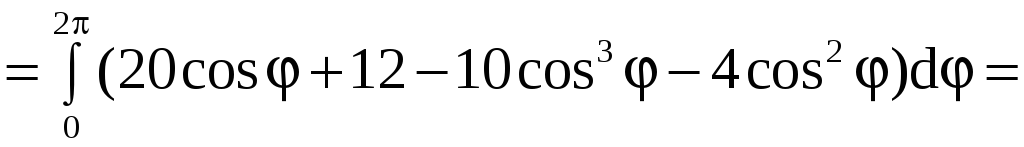
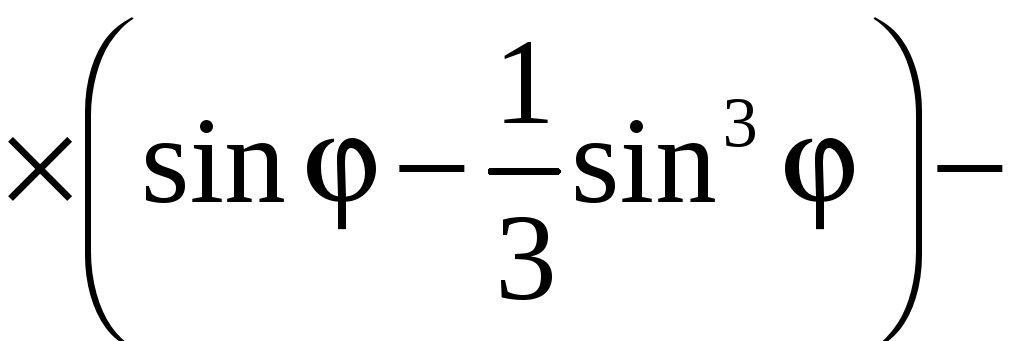
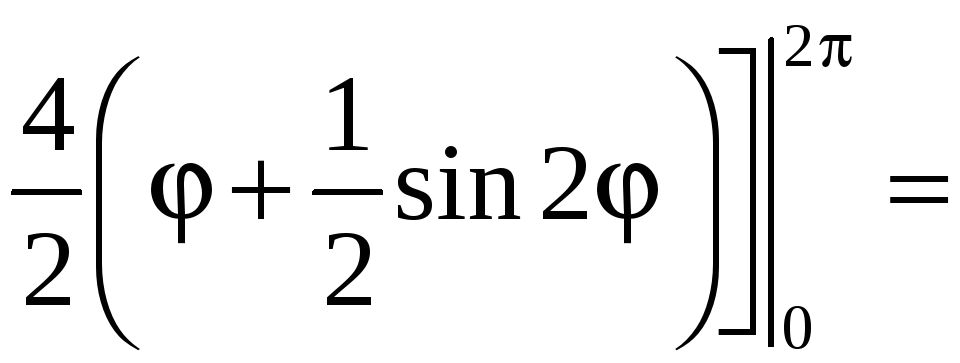
Пример 11. Вычислите тройной интеграл

где область (Т) задана условиями:

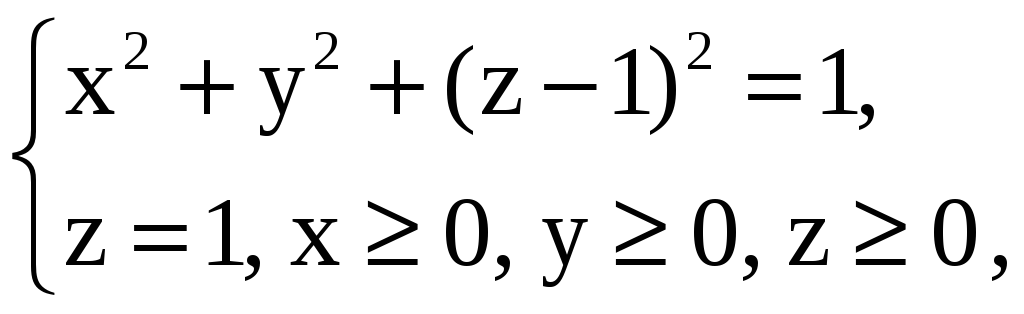
перейдя к сферической системе координат.

Р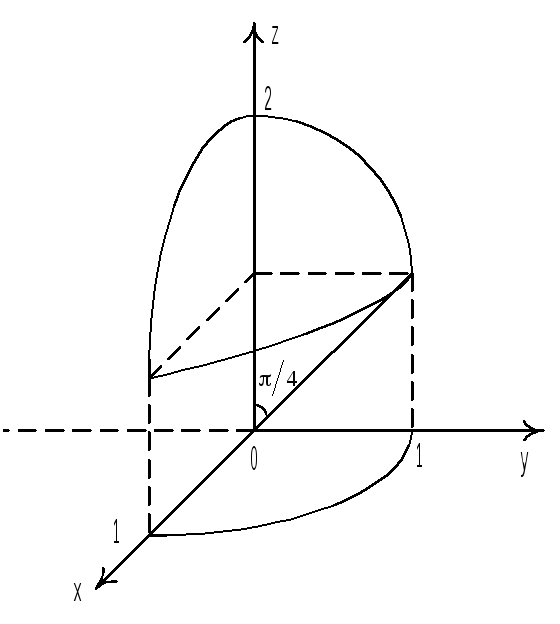ешение. Область, на которую распространяется данный интеграл, изображена на рисунке – это часть шара срезанная плоскостью z =1. Проекцией (Т) на плоскость 0xy является четверть круга радиусом 1 с центром в начале координат, расположенная в первой четверти. Перейдем к сферической системе координат:

J = ²sin. Переменные , ,  меняются в следующих пределах:

0    , 0    4, 1cos    2cos, где  = 1cos,  = 2cos –уравнения плоскости z = 1 и сферы x² + y² + (z – 1)² = 1 соответственно в сферической системе координат. В самом деле, запишем уравнения плоскости z = 1 и сферы x² + y² + (z – 1)² = 1 в сферической системе координат.

Применяя формулу (9), получим
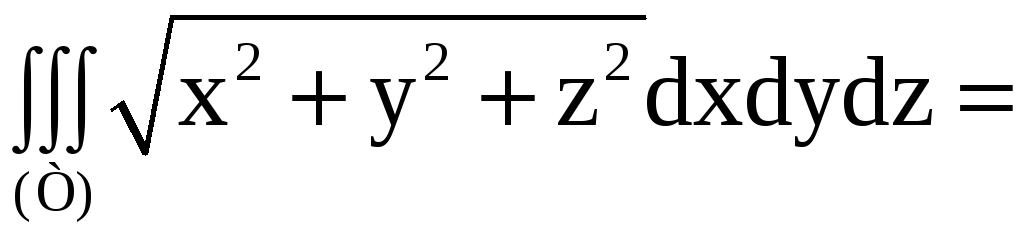
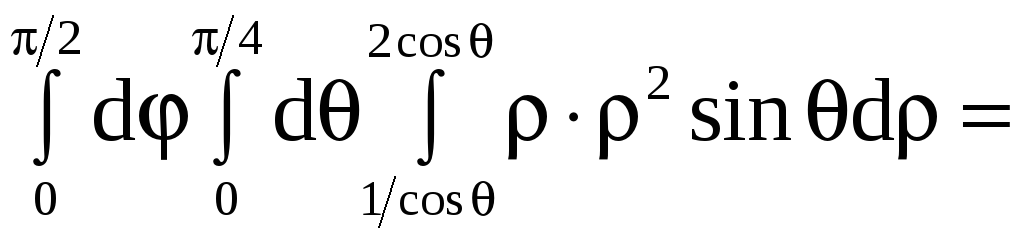
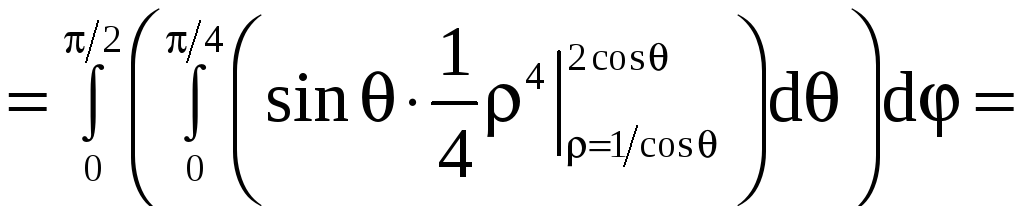
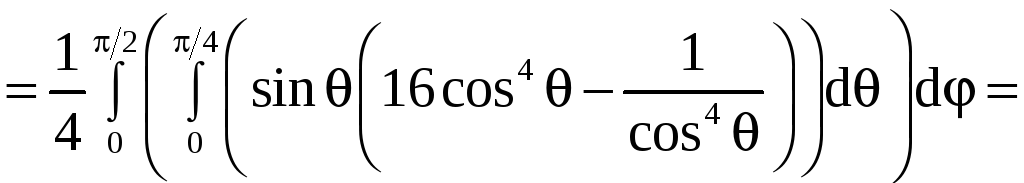
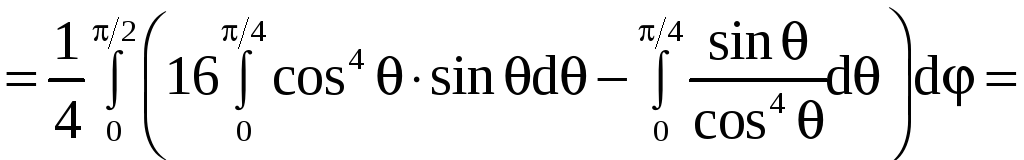
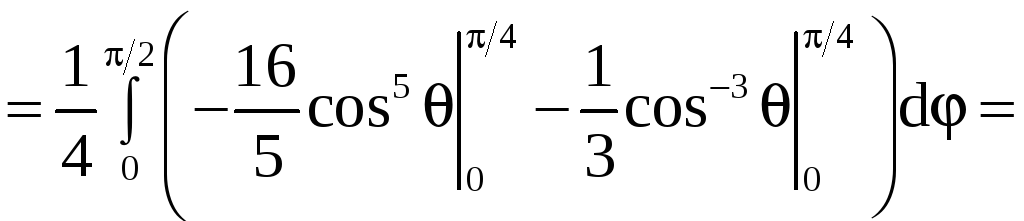
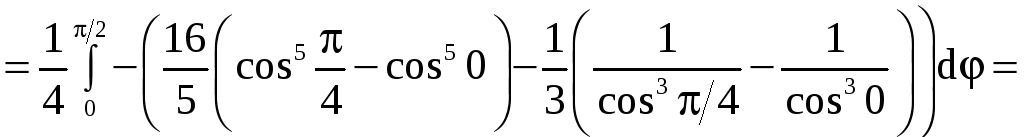
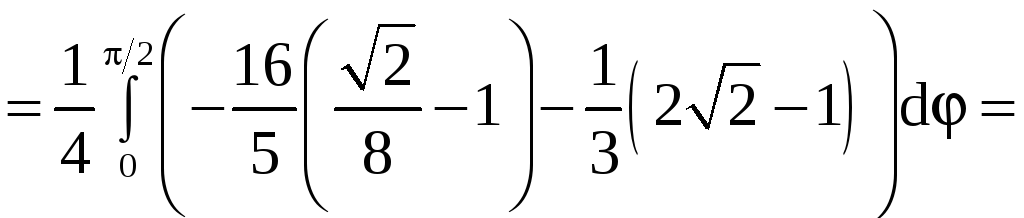
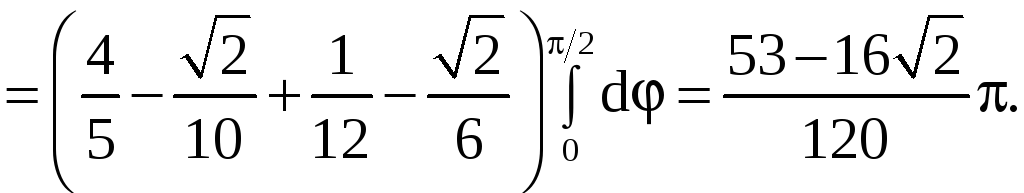