12.4 Линейные дифференциальные уравнения первого порядка

Уравнение вида (8) называется линейным ( у и у ‘ входят в первых степенях, не перемножаясь между собой).

Если , то это уравнение называется линейным неоднородным, а если - линейным однородным.

Общее решение однородного уравнения легко получается разделением переменных; разделяя переменные в уравнении , находим последовательно

, или, наконец, , где С – произвольная постоянная.

Общее решение неоднородного линейного уравнения можно найти исходя из общего решения соответствующего однородного уравнения по методу Лагранжа,

(Жозеф Луи Лагранж (1736-1813) родился в Турине в итало-французской семье. 19 лет от роду он стал профессором математики артиллерийской школы в Турине. Создатель вариационного исчисления. Наиболее значительный труд «Аналитическая механика»)

варьируя произвольную постоянную, т.е. полагая , где – некоторая, подлежащая определению, дифференцируемая функция от х. Для нахождения подставляем у в исходное уравнение, что приводит к уравнению , отсюда , где С – произвольная постоянная.

Тогда искомое общее решение неоднородного уравнения будет иметь вид .

Линейные уравнения первого порядка можно интегрировать также методом Бернулли, который заключается в следующем.

Полагая , где u, v – две неизвестные функции, преобразуем исходное уравнение к виду или .

Пользуясь тем. Что одна из неизвестных функций (например v) может быть выбрана совершенно произвольно (поскольку лишь произведение должно удовлетворять исходному уравнению) принимают за v любое частное решение уравнения (например, ), обращающее, следовательно, в нуль коэффициент при u в последнем уравнении.

Предыдущее уравнение приведется тогда к уравнению или , из которого находим u: . Умножая u на v, находим для решения исходного уравнения прежнее выражение .

Замечание 4. На практике поступают следующим образом: вводят подстановку (9). Эта подстановка (9) приводит уравнение (8) к уравнению с разделяющимися переменными.

Пример 5. Решить дифференциальное уравнение .

Значит, делаем подстановку +

, а сокращая на и разделяя переменные . Возвращаясь к подстановке .

Другой способ (метод Лагранжа)

Ищем решение соответствующего однородного уравнения

делим на y

=> интегрируя, получаем

=> ( обозначим вновь через С)

Ищем решение исходного неоднородного уравнения в виде , где - неизвестная функция. Подставляя в исходное уравнение

Сокращая на , , подставляя это значение в (*), получаем .

Уравнение вида называется уравнением Бернулли, так как (при уравнение является линейным, а при - уравнение с разделяющимися переменными).

После умножения его обеих частей на и подстановки , где z – новая искомая функция, оно приводится к линейному.

Преобразование уравнения Бернулли в линейное будем проводить в такой последовательности:

1) Умножим обе части уравнения на

2) Введем подстановку . Обе части этого равенства продифференцируем:

3) Полученное уравнение проинтегрируем как линейное с помощью подстановки

4) Возвращаемся к искомой функции, заменяя z на .

Пример 6.

Умножим обе части на

Делаем подстановку

( делим на 2 )

. См. предыдущий пример

Общий интеграл . Возвращаясь к искомой функции:

Замечание 5. На практике при решении уравнений Бернулли их не сводят к линейным, а интегрируют подстановкой или методом Лагранжа (метод вариации произвольной постоянной).

Уравнение Риккати по имени итальянского математика и инженера Я.Ф.Риккати (1676-1754) называют ОДУ вида (*), где – функции, непрерывные в некотором интервале изменения х. Это ОДУ содержит в себе частные случаи уже рассмотренных ранее уравнений: если , то (*) – линейное неоднородное уравнение ОДУ, а если - уравнение Бернулли с .

К сожалению, решение уравнения Риккати в общем случае не удается свести к операции интегрирования. Однако, если известно одно частное решение ОДУ (*), то его общее решение можно найти при помощи двух последовательных операций интегрирования.

Действительно, пусть - частное решение (*), выполнив подстановку получим

Так как - решение ОДУ (*), то окончательно имеем

Это уравнение Бернулли с . Заменой его можно свести к линейному неоднородному ОДУ, для нахождения общего решения которого достаточно выполнить последовательно две операции интегрирования.

Пример 7. Уравнение Риккати

Имеет частное решение . Замена приводит его к уравнению Бернулли Риккати . Положим ,тогда можно записать

Приравняв к нулю коэффициенты при u, получим ОДУ , имеющее частное решение . Теперь ОДУ для нахождения принимает вид

Разделяя переменные и интегрируя, получаем с учетом потерянного решения

и , где - первообразная функции .

В итоге исходное уравнение Риккати имеет решения 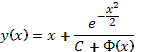и .

Замечание 6. Особых решений уравнение Риккати не имеет.