5.2.Множество Жюлиа
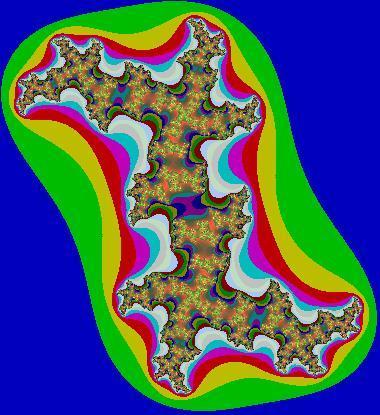
Рассмотрим
функцию
.
Множество Жюлиа определяется как граница
множества точек
,
стремящихся к бесконечности при
итерировании
:
Различные значения параметра
могут
порождать разнообразные множества
Жюлиа, причем малейшее изменение этого
параметра нередко приводит к существенным
метаморфозам.
Формула итераций для фрактала Джулия такая:
zk+1=zk2 + с ,
program J2;
uses Graph, Crt;
type
TComplex = record
X : Real;
Y : Real;
end;
const
iter = 50;
max = 16;
var
z, t, c : TComplex;
x, y, n : Integer;
Cancel : Boolean;
gd, gm : Integer;
mx, my : Integer;
begin
Cancel := false;
Randomize;
gd := Detect;
InitGraph(gd,gm,'c:\bp\bgi');
Mx := GetMaxX div 2;
My := GetMaxY div 2;
for y := -my to my do
for x := -mx to mx do
begin
n := 0;
z.x := x * 0.005;
z.y := y * 0.005;
c.x := 0.11;
c.y := -0.66;
while (sqr(z.x) + sqr(z.y) < max) and (n < iter) do
begin
t := z;
{z^2 + c}
z.x := sqr(t.x) - sqr(t.y) + c.x;
z.y := 2*t.x*t.y + c.y;
Inc(n);
if keypressed then
cancel := true;
end;
if n < iter then
begin
PutPixel(mx + x,my + y,16 - (n mod 16));
end;
if cancel then
exit;
end;
Readkey;
CloseGraph;
end.
При
множество
Жюлиа превращается в дендрит:
Другие формулы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.3. Фрактал Ньютона
Области
с фрактальными границами появляются
при приближенном нахождении корней
нелинейного уравнения
алгоритмом
Ньютона на комплексной плоскости. Для
функции действительной переменной
метод Ньютона часто называют методом
касательных. Поясним суть этого метода.
Пусть
нам задана функция
,
для которой известно приближенное
значение ее корня
,
а также значение функции в этой точке
и
значение её первой производной
.
Тогда, проводя касательную к графику
функции
в
этой точке и определяя ее пересечение
с осью
,
мы получим уточненное положение корня
.
Т.
к. уравнение касательной к
в
точке
выглядит
следующим образом:
то, приравнивая
нулю,
получаем, что уточненное значение корня
связано
с предыдущим значением
соотношением
Беря теперь значение
в
качестве приближенного и повторяя эту
процедуру, находим следующее приближение
корня
и
т. д. При некоторых условиях эта
последовательность сходится к корню
уравнения
.
Рассмотрим
теперь комплексный случай. Рассмотрим
уравнение
и
последовательность
Пусть
.
Как известно, это уравнение имеет три
корня
,
,
.
При выборе различных
процесс
будет сходится к различным корням.
Обозначим эти области притяжения через
.
Артур Кэли поставил задачу описания
областей
.
Оказывается границы этих областей имеют
фрактальную структуру.
program N3;
uses Graph, Crt;
type
Complex = Record
x : Real;
y : Real;
end;
const
iter = 50;
max = 1e+6;
min = 1e-6;
var
z, t, d : Complex;
p : Real;
x, y, n : Integer;
Cancel : Boolean;
gd, gm : Integer;
mx, my : Integer;
begin
Cancel := False;
Randomize;
gd := Detect;
InitGraph(gd,gm,'c:\bp\bgi');
Mx := GetMaxX div 2;
My := GetMaxY div 2;
for y := -my to my do
for x := -mx to mx do
begin
n := 0;
z.x := X * 0.005;
z.y := Y * 0.005;
d := z;
while (sqr(z.x)+sqr(z.y) < max) and (sqr(d.x)+sqr(d.y) > min)
and (n < iter) do
begin
t := z;
{z^3 - 1}
p := sqr(sqr(t.x)+sqr(t.y));
z.x := 2/3*t.x + (sqr(t.x)-sqr(t.y))/(3*p);
z.y := 2/3*t.y*(1-t.x/p);{}
d.x := abs(t.x - z.x);
d.y := abs(t.y - z.y);
Inc(n);
if keypressed then
Cancel := true;
end;
PutPixel(mx + x,my + y,16 - (n mod 16));
if cancel then exit;
end;
Readkey;
CloseGraph;
end.
Существуют и другие примеры алгебраических фракталов, например, биоморфы, дерево Барнсли, лямбда-фрактал (вариант множеств Мандельброта и Жюлиа), горящий корабль, паук.
6. L-системы
Понятие L-систем, тесно связанное с самоподобными фракталами, появилось только в 1968 году благодаря Аристриду Линденмайеру. Изначально L-системы были введены при изучении формальных языков, а также использовались в биологических моделях селекции. С их помощью можно строить многие известные самоподобные фракталы, включая снежинку Коха и ковер Серпинского. Некоторые другие классические построения, например кривые Пеано (работы Пеано, Гильберта, Серпинского), также укладываются в эту схему. И конечно, L-системы открывают путь к бесконечному разнообразию новых фракталов, что и послужило причиной их широкого применения в компьютерной графике для построения фрактальных деревьев и растений. Рассмотренные L-системы ограничиваются случаем детерминированных L-систем и графикой на плоскости.
Для графической реализации L-систем в качестве подсистемы вывода используется так называемая тертл-графика (turtle – черепаха). При этом точка (черепашка) движется по экрану дискретными шагами, как правило прочерчивая свой след, но при необходимости может перемещаться без рисования. В нашем распоряжении имеются три параметра (x,y,a), где (x,y) --- координаты черепашки, a --- направление, в котором она смотрит. Черепашка обучена интерпретировать и выполнять последовательность команд, задаваемых кодовым словом, буквы которого читаются слева направо. Кодовое слово представляет собой результат работы L-системы и может включать следующие буквы:
F --- переместиться вперед на один шаг, прорисовывая след.
b --- переместиться вперед на один шаг, НЕ прорисовывая след.
[ --- открыть ветвь (подробнее см. ниже)
] --- закрыть ветвь (подробнее см. ниже)
+ --- увеличить угол a на величину q
- --- уменьшить угол a на величину q
Размер шага и величина приращения по углу q задаются заранее и остаются неизменными для всех перемещений черепашки. Если начальное направление движения а (угол, отсчитываемый от положительного направления оси Х) не указано, то полагаем а равным нулю.
Несколько примеров иллюстрируют применение команд ветвления (обозначаются ],[) и вспомогательных переменных (обозначаются X, Y, и т.д.). Команды ветвления используются для построения деревьев растений, а вспомогательные переменные заметно облегчают построение некоторых L-систем.
Формально, детерминированная L-система состоит из алфавита, слова инициализации, называемого аксиомой или инициатором, и набора порождающих правил, указывающих, как следует преобразовывать слово при переходе от уровня к уровню (от итерации к итерации). К примеру, можно заменять букву F при помощи порождающего правила newf = F-F++F-F, что соответствует L-системе для снежинки Коха, рассматриваемой ниже. Символы +, -, ], [ не обновляются, а просто остаются на тех местах, где они встретились. Обновление букв в данном слове предполагается одновременным, то есть буквы слова одного уровня обновляются раньше любой буквы следующего уровня.
L-система, соответствующая снежинке Коха, задается следующим образом:
p = /3
Аксиома: F++F++F
Порождающее правило: newf = F-F++F-F
Графическое представление аксиомы F++F++F --- равносторонний треугольник. Черепашка делает один шаг вперед, затем угол а увеличивается на 2/3 и черепашка делает еще один шаг.
На первом шаге каждая буква F в слове-инициаторе F++F++F заменяется на F-F++F-F:
(F-F++F-F)+(F-F++F-F)+(F-F++F-F)
Повторяя этот процесс, на втором шаге получим:
F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F+F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F+ F-F++F-F- F-F++F-F++F-F++F-F-F-F++F-F
и т.д. Причем, убедившись на собственном опыте программирования L-систем знаю, что для снежинки Коха на 20-й итерации порождающее правило занимает несколько мегабайт текста !
Вот еще некоторые фракталы, построенные с использованием L-системы:
Рис. Дракон Хартера-Хатвея после 12-ти итераций
и его L-система:
p = /4
Аксиома: FX
Порождающее правило: newf = F
newx = X+YF+
newy = -FX-Y
Рис. Дерево после 5-ти итераций
и его L-система:
p = /7
Аксиома: F
Порождающее правило: newf = F[+F]F[-F]F
Рис. Квадрат Госпера после 2-х итераций [2]
и его L-система:
p = /2
Аксиома: -FX
Порождающее правило: newf = F
newx=+FYFY-FX-FX+FY+FYFX+FY-FXFX-FY-FX+FYFXFX-FY-FXFY+FY+FX-FX-FY+FY+FXFX
newy=FYFY-FX-FX+FY+FY-FX-FXFY+FX+FYFYFX-FY+FX+FYFY+FX-FYFX-FX-FY+FY+FXFX-