ФЕДЕРАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

Государственное образовательное учреждение высшего профессионального образования

“Российская таможенная академия”

Санкт-Петербургский имени В.Б. Бобкова филиал

Российской таможенной академии

_____________________________________________________

Кафедра информатики и информационных таможенных технологий

Н.В. Кожусь

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

по дисциплине "Математика"

Часть 2

Санкт-Петербург

2009

Основные формулы, термины и определения

Раздел "Дифференциальное исчисление функции одной переменной"

1. Производной функции в точке x₀ называется предел отношения приращения этой функции к приращению аргумента, при стремлении приращения аргумента к нулю.

Обозначения производной: .

По определению производной:

, (1)

или, в других обозначениях:

(1)′

2. Операция нахождения производной данной функции называется дифференцированием функции. Если существует конечный предел (1), то говорят, что функция дифференцируема в данной точке (имеет производную).

3. Основные правила дифференцирования

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций т.е.:

. (2)

Производная произведения двух дифференцируемых функций равна произведению производной первой функции на вторую функцию плюс произведение производной второй функции на первую функцию, т.е.:

(3)

Следствие 1. Постоянный множитель можно выносить за знак производной, т.е.:

. (4)

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные, т.е.:

´ (5)

Производная частного двух дифференцируемых функций определяется формулой:

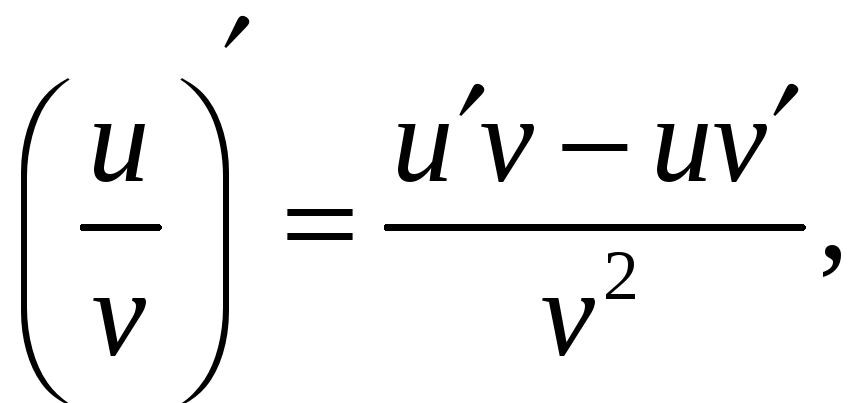где (6)

Таблица1.

4. Таблица производных основных элементарных функций

№п/п	Производная	№п/п	Производная
1		8
2		9
3		10
4		11
5		12
6		13
7		14

5. Сложной функцией называется функция от функции, т.е. функция вида:

, (7)

где , ,

u ­ промежуточный аргумент, x – независимая переменная.

6. Теорема. Если и – дифференцируемые функции своих аргументов, то производная сложной функции существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.:

(8)

6. Производная от первой производной функции называется второй производной или производной второго порядка и обозначается как или .

По определению

. (9)

7. Производной n-ого порядка функции (n-й производной) называется производная от (n – 1) –ой производной:

. (10)

8. Дифференциалом функции называется главная линейная часть приращения функции .

Обозначение дифференциала – или .

По определению

или . (11)

Можно показать, что , тогда

. (11)′

Таким образом, дифференциал функции численно равен произведению производной этой функции на дифференциал независимой переменной.

9. Теорема. Если функция непрерывна на отрезке [a, b] и дифференцируема в интервале (a,b), причем () для , то эта функция возрастает (убывает) на отрезке [a, b].

Таким образом, знак производной позволяет определить, возрастает или убывает функция в заданном интервале:

если (функция возрастает); (14)

если (функция убывает). (15)

10 Экстремумами называют локальные максимумы и минимумы функции.

11. Теорема. Необходимый признак существования экстремума. Если функция имеет экстремум в точке , то ее производная в этой точке равна нулю или не существует.

12. Точки, в которых производная равна нулю или не существует, называются стационарными (или критическими) точками производной.

13. Теорема. Первый достаточный признак существования экстремума. Если в точке x = x₀ производная функции равна нулю и меняет знак при переходе через эту точку, то точка x₀ является точкой экстремума, причем:

x₀ – точка максимума, если знак меняется с плюса на минус;

x₀ – точка минимума, если знак меняется с минуса на плюс.

14. Теорема. Второй достаточный признак существования экстремума. Если в точке x₀ первая производная функции обращается в нуль, а ее вторая производная отлична от нуля, то в точке x₀ функция достигает экстремума (минимума, если y(x₀)>0, и максимума, если y(x₀)<0).

15. Теорема. Если во всех точках интервала (a, b) вторая производная функции отрицательна (положительна), то кривая на этом интервале выпукла (вогнута).

16. Точка кривой, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба кривой.

17. Необходимое условие существования точки перегиба. Если кривая имеет перегиб в точке , то вторая производная функции в этой точке равна нулю или не существует.

18. Достаточное условие существования точки перегиба. Если в точке вторая производная обращается в нуль и меняет знак при переходе через нее, то – точка перегиба кривой .

19. Правило Лопиталя. Если функции и дифференцируемы в окрестности точки , обращаются в нуль в этой точке, и существует предел отношения при , то существует и предел отношения самих функций, равный отношению производных, т.е.:

. (16)

Замечания:

- правило Лопиталя применяется для раскрытия неопределенностей типа или .

- правило Лопиталя (16) справедливо и для случая, когда .

- правило Лопиталя можно применять повторно, несколько раз.