ВВЕДЕНИЕ
В МАТЕМАТИЧЕСКИЕ ВЫЧИСЛЕНИЯ
В СИСТЕМЕ MAPLE
(часть 4)
Тема 11. Реализация методов оптимизации в системе Maple
Средства оптимизации
Рассмотрим как в системе Maple можно
научиться решать задачи нахождения
экстремумов функции
,
ее наибольшего и наименьшего значения
на множестве.
Для этого необходимо использовать библиотеку extrema, помощью которой возможно находить локальные экстремумы функции, ее наибольшее и наименьшее значения.
Команда extrema(expr,constrs,vars,’s’) находит экстремумы функции по заданным переменным. Здесь expr - функция, экстремум которой необходимо найти, vars – переменная (группа переменных в фигурных скобках), по которой ведется поиск, ограничения поиска задаются переменной constrs (могут отсутствовать), а в переменную ’s’ присваиваются найденные координаты точек экстремума, записанные в виде множества точек, ограниченного фигурными скобками (эта переменная также может отсутствовать).
В ранних версиях системы Maple перед тем, как приступить к работе с этой функцией требовалось предварительно объявить ее при помощи reаdlib(extrema), но уже с Maple 7/8 команду extrema можно использовать без предварительного объявления.
Пример:
>restart:
>extrema(abs(x^2-2),x);
В этом примере был найден локальный
максимум функции
,
равный 2.
Команды minimize(expr,vars,ranges) и maximize(expr,vars,ranges) - вычисляют наименьшее и наибольшее значения функции соответственно. Поиск может производится как на всей числовой прямой, так и на заданном отрезке (ranges - интервал, в котором изменяется vars).
Для функций нескольких переменных вычисляются максимумы и минимумы по отдельным переменным.
Пример:
> minimize(x^2+y^2+3);
> minimize(x^2+y^2,x);
> minimize(x^2+y^2,y);
> minimize(x^2+y^2,x=10..100,y=10..100);
> maximize(x*exp(-x),location);
В последнем примере использован параметр location, обеспечивающий расширенный вывод результатов поиска – выдается не только найденное значение максимума, но и значения переменной (переменных) в этой точке:
> minimize(x^2-2*x+y^2-4*y+5,x=-100..100,y=-1000..1000,location);
Решение типовых задач линейного программирования (применение симплекс-метода) Задача о смеси
Для ряда несложных и хорошо изученных математических моделей основное требование задачи заключается в нахождении смеси веществ, продуктов и тому подобного, удовлетворяющих определенным технологическим требованиям. Такие задачи изучаются методами линейного программирования.
Прародительницей этих задач была так называемая задача о диете: найти наиболее дешевую смесь пищевых продуктов под номерами 1,2,…,n (хлеба, мяса, молока и т.п.), которая удовлетворяла бы определенным биологическим ограничениям на содержание жиров, белков, углеводов, микроэлементов, витаминов и тому подобных биологически активных веществ.
Если обозначить через
процентное содержание (по весу) j-го
продукта в смеси, через
- весовое содержание i-го
вещества в j-ом
продукте,
- допустимую верхнюю границу содержания
i-го вещества в смеси,
- нижнюю, а через
- стоимость j-го
продукта, то задача о наиболее дешевой
диете приобретает вид:
(1)
(2)
Функция
,
минимум которой ищется в (1), называется
целевой функций.
Для приведенной задачи характерно наличие двусторонних ограничений (2) на значение определенных линейных комбинаций переменных. Эта особенность весьма часто встречается в практике линейного программирования и специальным образом учитывается как в алгоритмах, так и в формах представления данных.
Приведенная интерпретация задачи (1)-(2) имеет скорее учебно-педагогическое, чем реально-практическое значение. В действительности, вместо продуктов питания здесь могут выступать, к примеру, различные виды нефти, полученные с различных нефтяных месторождений.
Эти виды продукции отличаются по составу: они содержат различные концентрации примесей серы, парафинов, воды и прочих веществ, существенно влияющих на процесс термического разложения нефти на бензины, керосин и другие нефтепродукты.
Для наилучшей эффективности и безопасности технологического процесса концентрации вышеупомянутых примесей должны находиться в определенных пределах, что достигается смешиванием различных видов сырой нефти. Учитывая, что стоимости различных видов нефти существенно отличаются, задача подбора наиболее дешевой смеси, укладывающейся в технологические допуски, может дать существенный экономический эффект, преумноженный многомиллионными объемами переработки.
Аналогичные проблемы возникают, например, при производстве металлургического кокса из углей различных месторождений, разработке оптимального рациона питания и т.п. В более реалистичных постановках возникают также и так называемые производственно-транспортные задачи, когда в расходах (2) учитывают транспортные затраты.
В различных постановках задач линейного программирования допустимое множество решений может описываться разными способами: системами неравенств различных знаков, наборами равенств и, наконец, комбинациями равенств и неравенств. Такое разнообразие описаний является, с точки зрения теории, определенным недостатком, так как вынуждает каждый тип описания рассматривать по-своему.
Однако все варианты постановок задачи линейного программирования могут быть сведены к задаче линейного программирования, содержащей лишь равенства и условия неотрицательности искомого решения (приведем формулировку этой задачи в матрично-векторной форме):
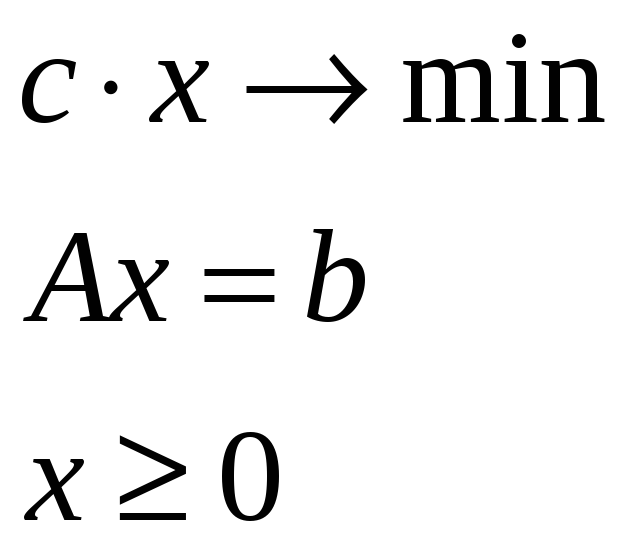(3)
Такая формулировка задачи линейного программирования (3) называется стандартной или канонической.
Сведения к стандартной форме задачи линейного программирования осуществляется как правило, в зависимости от первоначальной формулировки, с помощью не очень сложных приемов.
Задачи линейного программирования решаются симплекс-методом.
В системе Maple решение задач линейного программирования реализовано на основе функций maximize и minimize, входящих в пакет линейной оптимизации simplex и реализующих алгоритм симплекс-метода.
Необходимо отметить, что задачи линейной оптимизации важны как в фундаментальных, так и в прикладных приложениях математики. В пакете simplex имеется небольшой, но достаточно представительный набор функций и определений, предназначенный для решения таких задач.
> with(simplex);
Приведем краткое назначение этих функций:
-
basis — возврат списка основных переменных для множества линейных уравнений;
-
convexhull — вычисление выпуклой оболочки для набора точек;
-
cterm — задание констант для системы уравнений или неравенств;
-
define_zero — определение наименьшего значения, принимаемого за ноль (по умолчанию увязано со значением системной переменной Digits);
-
display — вывод системы уравнений или неравенств в матричной форме (см. далее);
-
dual — выдача сопряженных выражений;
-
feasible — выяснение возможности решения заданной задачи:
-
maximize — вычисление максимума функции (см. далее);
-
minimize — вычисление минимума функции (см. далее);
-
pivot — создание новой системы уравнений с заданным главным элементом;
-
pivoteqn — выдача подсистемы уравнений для заданного главного элемента;
-
pivotvar — выдача переменных с положительными коэффициентами в целевой функции;
-
ratio — выдача отношений для определения наиболее жесткого ограничения;
-
setup — задание системы линейных уравнений;
-
standardize — приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно» (см. далее).
Команда maximize(f,c,vartype) вычисляет максимальное значение функции f при заданных условиях, где f - линейная функция, которую необходимо максимизировать, c - список линейных ограничений. Команда maximize возвращает множество значений, систему линейных уравнений, пустое множество или NUUL, если количество решений задачи неограниченно.
Команда minimize(f,c,vartype) вычисляет минимальное значение, ее использование аналогично полностью аналогично использованию команды maximize.
Пример:
> restart: with(simplex):
> minimize(x-y,{4*x+3*y>=5,3*x+4*y<=4});
Команда display(c) отображает набор уравнений или неравенств в матричной форме:
> display({x+3*y+z<=0,w-2*y-z<=2});
Команда standardize(c) переводит набор линейных уравнений в линейные неравенства:
> standardize({3*x+4*y<=4,4*x+3*y=5});
