
Тема. Компактність у метричних просторах. Критерій компактності в різних метричних просторах.
1. Компактність.
Означення:
Множина
![]() в метричному просторі
в метричному просторі
 називається компактною,
якщо з будь-якої нескінченої підмножини
називається компактною,
якщо з будь-якої нескінченої підмножини
![]() можна виділити послідовність
можна виділити послідовність
![]() ,
що збігається до деякої границі
,
що збігається до деякої границі
![]() .
.
Означення:
Множина
![]() ,
що
лежить в
деякому
метричному просторі
,
що
лежить в
деякому
метричному просторі
![]() ,
називається
передкомпактною,
чи
відносно
компактною,
якщо
його
замикання
в
,
називається
передкомпактною,
чи
відносно
компактною,
якщо
його
замикання
в
![]() компактно.
компактно.
Означення:
Множина
![]() називається
обмеженою,
якщо
вона
міститься
в деякій
кулі.
називається
обмеженою,
якщо
вона
міститься
в деякій
кулі.
Твердження: Будь-яка компактна множина є замкненою.
Доведення.
У метричному просторі будь-яка
підпослідовність збіжної послідовності
збігається до тієї же границі, отже
границя послідовності також належить
множині
![]() , тобто множина
, тобто множина
![]() замкнена.
замкнена.
Теорема:
Будь-яка
відносно
компактна
множина
![]() ,
що
лежить в
деякому
метричному
просторі
,
що
лежить в
деякому
метричному
просторі
![]() ,
є
обмеженою.
,
є
обмеженою.
Доведення.
Припустимо,
що множина
![]() є
відносно компактною,
але не обмеженою, і нехай
є
відносно компактною,
але не обмеженою, і нехай
![]() це
довільна точка з
це
довільна точка з
![]() . Тому що
. Тому що![]() не
обмежена, то існує точка
не
обмежена, то існує точка
![]() ,яка
лежить поза кулею
,яка
лежить поза кулею
![]() .
Покладемо
.
Покладемо
![]() .
Тому що
.
Тому що
![]() не
обмежена, то
не
обмежена, то
![]() .
Покладемо
.
Покладемо
![]() і
далі. Отримаємо послідовність
і
далі. Отримаємо послідовність
![]() ,
що
,
що
![]() ,
якщо
,
якщо
![]() ,
яка не містить
жодної
збіжної підпослідовності, що суперечить
відносної компактності множини
,
яка не містить
жодної
збіжної підпослідовності, що суперечить
відносної компактності множини
![]() .
.
Означення:
Простір
 називається компактним
( компактом ),
якщо будь-яка нескінчена підмножина
простору
називається компактним
( компактом ),
якщо будь-яка нескінчена підмножина
простору
 містить послідовність, що збігається
до деякого елементу з
містить послідовність, що збігається
до деякого елементу з
 .
.
Можна довести, що компакт є повним метричним простором.
Приклади компактних і не компактних множин.
-
Нехай
 з метрикою, яка задана в просторі
з метрикою, яка задана в просторі
 ,
тоді за теоремою Больцано-Веєйрштраса
,
тоді за теоремою Больцано-Веєйрштраса
 буде
компактним.
буде
компактним.
-
Простір
 не компактний , тому що в ньому множина
не компактний , тому що в ньому множина
 не
містить жодної збіжної підпослідовності.
не
містить жодної збіжної підпослідовності. -
Простір
 не
компактний, аналогічно
не
компактний, аналогічно
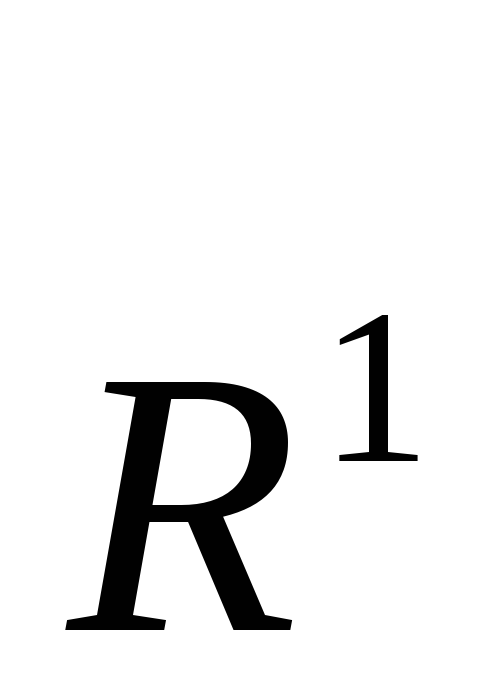 ,
але будь-яка замкнена обмежена множина
є компактною за теоремою Больцано-Веейрштрасса
.
,
але будь-яка замкнена обмежена множина
є компактною за теоремою Больцано-Веейрштрасса
. -
В просторі
 всякий відрізок
всякий відрізок
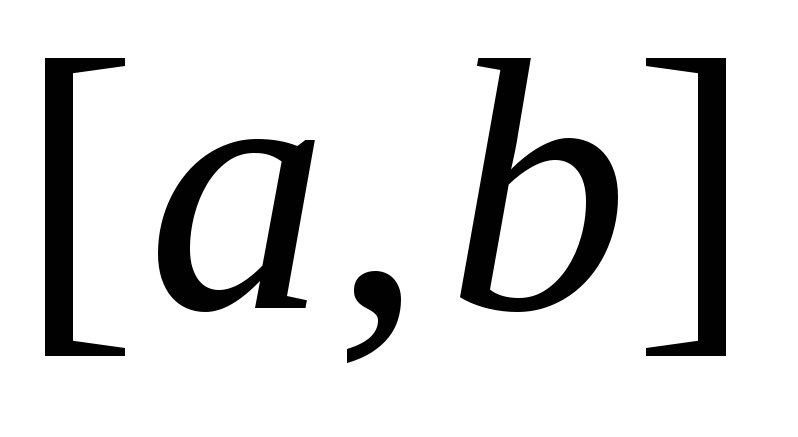 буде компактний, тому що простір скінчено
вимірний, а даний відрізок є замкненою
і обмеженою множиною (За теоремою
Больцано-Веейрштрасса в скінчено
вимірному просторі будь-яка замкнена
обмежена множина є компактною).
буде компактний, тому що простір скінчено
вимірний, а даний відрізок є замкненою
і обмеженою множиною (За теоремою
Больцано-Веейрштрасса в скінчено
вимірному просторі будь-яка замкнена
обмежена множина є компактною).
-
Простір
 не компактний , більше того, в ньому
існують обмежені замкнені, але не
компактні, множини.
не компактний , більше того, в ньому
існують обмежені замкнені, але не
компактні, множини. -
Простір
 не
компактний ,
в
ньому існують обмежені замкнені, але
не компактні, множини. Такою множиною
є одинична куля
не
компактний ,
в
ньому існують обмежені замкнені, але
не компактні, множини. Такою множиною
є одинична куля
 .
Дійсно, розглянемо таку послідовність
точок з
.
Дійсно, розглянемо таку послідовність
точок з
 :
:
 ,
,
 ,
... ,маємо
,
... ,маємо
 при
при
 .
Тому послідовність
.
Тому послідовність
 та всяка її підпослідовність не
збігається, що і доводить не компактність
кулі
та всяка її підпослідовність не
збігається, що і доводить не компактність
кулі
 .
. -
Прикладом компактної множини у просторі
 є основний паралелепіпед координатного
гільбертова простору, який представляє
з себе сукупність точок
є основний паралелепіпед координатного
гільбертова простору, який представляє
з себе сукупність точок
 ,
координати яких задовольняють умові
,
координати яких задовольняють умові
 .
Компактність цієї множини слідує з
загальної ознаки компактності у просторі
.
Компактність цієї множини слідує з
загальної ознаки компактності у просторі
 ,
(
,
( ).
).
В метричному просторі компактність тісно пов'язана з повною обмеженістю.
2. Повна обмеженість.
Нехай
![]() деяка
множина у метричному просторі
деяка
множина у метричному просторі
 ,
,
![]() - деяке додатне число.
- деяке додатне число.
Означення:
Множина
![]() з
з
 називається
називається
![]() -
сіткою
для множини
-
сіткою
для множини
![]() ,
коли для будь-якої точки
,
коли для будь-якої точки
![]() знайдеться
хоч би одна точка
знайдеться
хоч би одна точка
![]() ,така
що
,така
що
![]() ,
тобто
,
тобто
![]() .
.
Приклад,
ціле чисельні точки утворюють на площині
![]() -сітку.
-сітку.
Означення:
Множина
![]() називається цілком
обмеженою
(повністю
обмеженою),
якщо для будь-якого
називається цілком
обмеженою
(повністю
обмеженою),
якщо для будь-якого
![]() існує
скінчена
існує
скінчена
![]() -
сітка.(
-
сітка.(
![]() скінчена
скінчена
![]() -
сітка).
-
сітка).
Твердження: Цілком обмежена множина є обмеженою.
Доведення. Як сума скінченого числа обмежених множин.
Обернене в загальному випадку не вірне.
Зауваження.
Якщо множина
![]() цілком обмежена,то її замикання
цілком обмежена,то її замикання
![]() також
цілком обмежене.
також
цілком обмежене.
Твердження:
Якщо
метричний простір
![]() повністю обмежений, то він сепарабельний.
повністю обмежений, то він сепарабельний.
Доведення.
Дійсно, побудуємо для кожного
![]() в
в
![]() скінчену
скінчену
![]() -
сітку. Сума їх по всім
-
сітку. Сума їх по всім
![]() представляє
з себе злічену всюди щільну множину в
представляє
з себе злічену всюди щільну множину в
![]() .
.
Приклади.
1. В
![]() -
вимірному метричному евклідовому
просторі повна обмеженість співпадає
з звичайною обмеженістю, тобто можливістю
помістити дану множину у велику кулю
або куб.
-
вимірному метричному евклідовому
просторі повна обмеженість співпадає
з звичайною обмеженістю, тобто можливістю
помістити дану множину у велику кулю
або куб.
Дійсно,
якщо зробити розбиття кубу на маленькі
кубики з ребром
![]() ,
то вершини цих кубиків будуть утворювати
скінчену
,
то вершини цих кубиків будуть утворювати
скінчену
![]() -
сітку в початковому кубі, отже і в
будь-якій множині, що знаходиться в
цьому кубі.
-
сітку в початковому кубі, отже і в
будь-якій множині, що знаходиться в
цьому кубі.
2.
Одинична сфера
![]() у
просторі
у
просторі
![]() є
прикладом обмеженої, але не цілком
обмеженої множини. Дійсно, розглянемо
точки
є
прикладом обмеженої, але не цілком
обмеженої множини. Дійсно, розглянемо
точки
![]() ,
,
![]() ,
,
![]() ,
,
... .
Тоді
![]() при
при
![]() .
Отже, в не може бути скінченої
.
Отже, в не може бути скінченої
![]() -
сітки для жодного
-
сітки для жодного
![]() .
.
3.
Розглянемо в просторі
![]() множину
множину
![]() точок
точок
![]() ,
,![]()
![]() ,
,![]() ,
... ,
,
... ,![]() , ... . Цю множину називають основним
паралелепіпедом або " гільбертовою
цеглою " простору
, ... . Цю множину називають основним
паралелепіпедом або " гільбертовою
цеглою " простору
![]() .
Це приклад нескінченно вимірної цілком
обмеженої множини.
.
Це приклад нескінченно вимірної цілком
обмеженої множини.
Доведення.
Нехай задане
![]() .
Оберемо
.
Оберемо
![]() , таке що
, таке що
![]() ,
,
тоді кожної точці
![]() (1)
(1)
з
![]() поставимо
у відповідність точку
поставимо
у відповідність точку
![]() (2)
(2)
з тієї ж множини.
Тоді
 .
.
Множина
![]() точок
виду
(2) з
точок
виду
(2) з
![]() цілком обмежена, як обмежена множина в
цілком обмежена, як обмежена множина в
![]() -
вимірному просторі. Оберемо в
-
вимірному просторі. Оберемо в
![]() скінчену
скінчену
![]() -
сітку. Зрозуміло, що вона буде також
-
сітку. Зрозуміло, що вона буде також
![]() -
сіткою в
-
сіткою в
![]() .
.
