11

Тема: Евклідові простори.

1.Скалярний добуток. Нерівність Коші-Буняковського. Приклади.

Існує добре відомий спосіб введення норми в лінійному просторі – це задати в ньому скалярний добуток.

Означення: Скалярним добутком у дійсному лінійному просторі є дійсна функція , визначена для кожної пари елементів і яка задовольняє наступним умовам:

1. ;

2. ;

3. ;

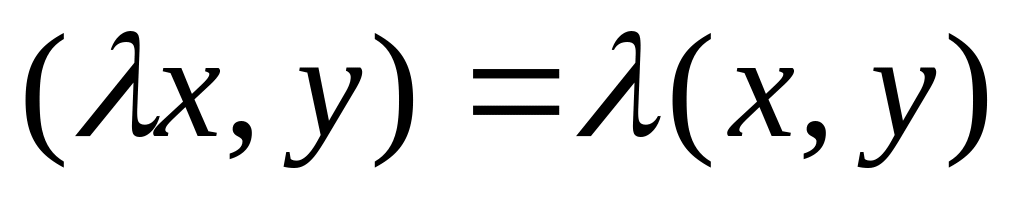4. , причому тільки при .

Означення: Лінійний простір з фіксованим у ньому скалярним добутком називається евклідовим простором.

В евклідовім просторі вводиться норма за допомогою формули .

Можна показати, що всі аксіоми норми в цьому випадку виконуються:

1. виконується,

;

2. ;

3. Щоб довести аксіому 2) норми(нерівність трикутника) використаємо нерівність Коші-Буняковського

. (1)

Доведемо нерівність Коші-Буняковського (1).

Розглянемо функцію . Тому що вона представляє квадрат деякого вектора, то , отже дискримінант квадратного трьохчлена .

Знайдемо дискримінант:

D = 4 ,отже .

Доведемо аксіому 2) норми, що

Теорема. В евклідовому просторі сума, добуток на число і скалярний добуток неперервні, тобто, якщо і (збіжність за нормою), (як числова послідовність), то

, та .

Доведення. Доведення цих фактів засновано на використанні нерівності Коші-Буняковського:

1)

Дійсно,

за ,

за ,

тоді :

, .

2) = +

= , для великих .

Дійсно, з того, що збігається до , слідує, що послідовність обмежена, тобто : ( ). Для великих можна зробити так, щоб та .

3) =

= , для великих , де - таке число, що (послідовність збіжна, тому що з того що слідує .

2. Ортогональні системи.

Скалярний добуток в R дозволяє ввести в цьому просторі не тільки норму (тобто довжину) вектора, але і кут між векторами; кут між векторами х і у визначається за формулою

cos (2)

При цьому з нерівності Коші-Буняковського випливає, що вираз, який стоїть в (2) праворуч, по модулю не більший за 1 і, звідси, формула (2) дійсно, для будь-яких ненульових і визначає деякий кут φ: 0 φ π.

Означення: Якщо , то з (2) одержимо, що φ= ; в цьому випадку вектори і називають ортогональними.

Система ненульових векторів з називається ортогональною, якщо , =0 при α β.

Твердження: Якщо вектори ортогональні, то вони лінійно незалежні.

Доведення.

Дійсно,нехай + +…+ =0; оскільки - ортогональна система, маємо ( , +…+ )= ( , )=0, але ( , ) 0 і звідси =0 для всіх і=1,2,…,n.

Означення: Якщо ортогональна система - повна (тобто найменший замкнений простір, що її містить, є весь ), то вона називається ортогональним базисом.

Взагалі, якщо система (повна або ні) така, що

то вона називаєься ортогональною нормованою (або ортонормованою) системою. Якщо - ортогональна система, то - ортогональна нормована система.

Означення: Якщо ортогональна система повна та норма кожного її елемента дорівнює одиниці, то вона називається ортогональним нормованим базисом.

Приклади.

Розглянемо деякі приклади евклідових просторів і ортогональних базисів в них.

1. n-вимірний арифметичний простір , елементами якого є системи дійсних чисел

х=(х ,…,х ) зі звичайними операціями додавання і множення на число і скалярним добутком

(3)

являє собою приклад евклідового простору. Ортогональний нормований базис у ньому (один з нескінченого числа можливих) утворюють вектори

е =(1,0,…,0),

е =(0,1,…,0),

……………..

е =(0,0,…,1).

2. Простір з елементами х = (х ,…,х ,…), де 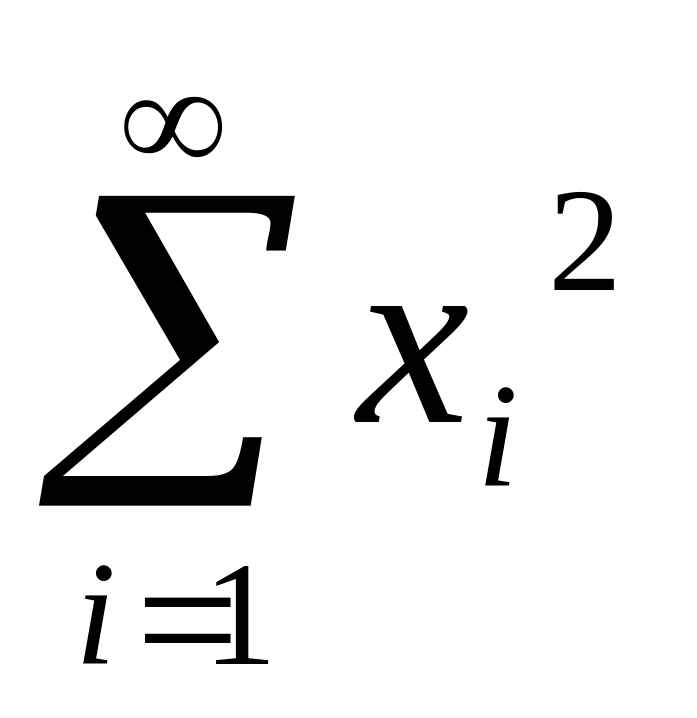< , і скалярним добутком

(4)

евклідів простір.

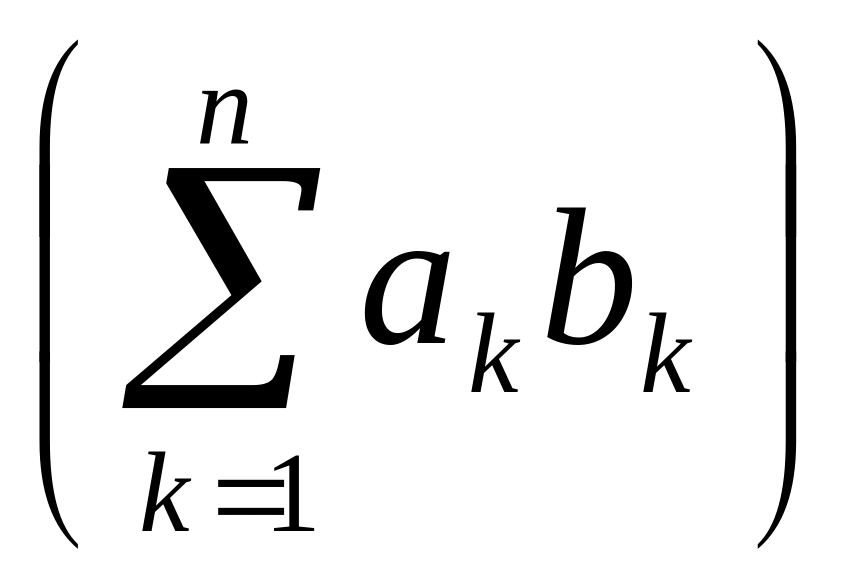
Дійсно, збіжність ряда, що стоїть в (4) праворуч випливає з нерівності Коші-Буняковського . Властивості 1-4 скалярного добутку перевіряються безпосередньо.

Найпростіший ортогональний базис у утворюють вектори

е =(1,0,0,…),

е =(0,1,0,…), (5)

е =(0,0,1,…),

……………..

Ортогональність і нормованість системи ясні, крім того система (5) повна: нехай х=(х ,…,х ,…) – будь-який вектор з і х =(х ,…,х ,0,0,…). Тоді х - лінійна комбінація векторів е ,…, е і при n 0.

3. Простір С [a, b], що складається з неперервних дійсних функцій на [a, b], зі скалярним добутком – евклідів простір.

(6)

Серед різноманітних базисів, що існують в ньому, можна вказати на тригонометричну систему, що складається з функцій

, , . (7)

Ортогональність системи перевіряється безпосередньо.

Якщо розглядаються неперервні функції на відрізку довжини 2 , наприклад [- , ], то відповідна тригонометрична система буде: ,cos(nt), sin(nt) (n=1,2,…).

Система (7) повна, тобто кожна неперервна функція може бути представлена у вигляді лінійної комбінації даних функцій.

Доведемо, що система (7) є повною.

Згідно з теоремою Вейєрштрасса всяка неперервна функція на відрізку [a, b], яка приймає на кінцях відрізка однакові значення, може бути представлена як границя рівномірно збіжної послідовності тригонометричних многочленів, тобто лінійних комбінацій елементів системи (7). Така послідовність і подавно збіжна до по нормі в просторі С [a, b]. Якщо ж функція f - довільна функція в С [a, b], то її можна подати, як границю (по нормі простору С [a, b]) послідовності функції , кожна з яких співпадає з f на відрізку [a,b- ], лінійна на [b- ,b] і в точці b приймає те значення, що і в a. Звідси, кожен елемент в C [a,b]можна приблизити як завгодно точно (в метриці цього простору) лінійними комбінаціями елементів системи (7), а це і означає її повноту.

f(x)