
- •Основные цели и задачи мат физики. Предмет и методы ее исследования.
- •2. Постановка краевой задачи поперечных колебаний тонкой струны.
- •Постановка краевой задачи продольных колебаний стержня.
- •4. Постановка краевой задачи стационарного обтекания тела идеальной жидкостью.
- •5. Постановка краевой задачи переноса тепла в неподвижной среде.
- •6. Классификация краевых задач мат физики. Общая постановка краевых задач мат физики. Понятие корректно и некорректно поставленной задачи.
- •7. Классификация диф ур-й 2 порядка с 2 независимыми переменными.
- •8. Приведение к каноническому виду уравнений гиперболического типа.
- •9. Приведение к каноническому виду уравнений параболического типа.
- •10. Приведение к каноническому виду уравнений эллиптического типа.
- •11. Уравнение Трикоми. Канонический вид ур-я Трикоми.
- •12. Классификация уравнений 2 порядка с числом независимых переменных больше 2.
- •13. Постановка задачи ш-л. Основные свойства собственных значений и собственных функций.
- •14. Основная идея и расчетная схема метода разделения переменных.
- •15. Задача ш-л для отрезка.
- •16. Задача ш-л для отрезка с периодическими граничными условиями.
- •17. Задача Штурма-Лиувиля для прямоугольника и прямоугольного параллелепипеда.
- •18. Задача ш-л для круга.
- •19. Задача ш-л для кругового сектора.
- •20. Задача ш-л для кругового кольца.
- •21. Задача ш-л для цилиндра.
- •22. Задача ш-л для шара.
- •23. Задача ш-л для шарового слоя.
-
Основные цели и задачи мат физики. Предмет и методы ее исследования.
Предметом мат физ является построение и исследование мат.мод. физического процесса и явления.
Этапы:

Большинство задач классической мат физ сводится к Д.У. и краевым задачам для этих уравнений – уравнений мат физ. Поэтому мат физ тесно связана с такими разделами математики как теория Д.У., теория функций, функциональный анализ, Т.В., приближенные методы и вычислительная математика.
Изучение мат мод квантовой физики потребовало привлечения таких новых областей математики, как теория обобщенных функций, теория функций многих комплексных переменных, геометрических, топологических, алгебраических и теоретико-числовых методов.
Важное место в современной мат физ занимает нелинейный анализ. Исследование нелинейных физических систем получило широкое распространение со второй половины XX века благодаря созданию и внедрению мощных средств вычислительной техники. Оказалось, что практически все физические явления нелинейны. Линейное приближение, исследуемое ранее, либо описывает очень частные случаи поведения физических систем, либо является чрезвычайно грубым.
Тем не менее, исследованию линейных физических систем по-прежнему уделяется значительное внимание, так как:
-
Линейные мат мод описывают большинство физических явлений, изученных до середины XX века.
-
Изучение методов постановки и решения линейных начально-краевых задач создает необходимую базу для дальнейшего исследования нелинейных систем.
В процессе исследования математической
модели представляется полезным
абстрагироваться от ее физического
содержания. Это связано с тем, что
совершенно различные по своей природе
процессы могут описываться одинаковыми
уравнениями. Например, уравнение
Пуассона 
в
зависимости от смысла, придаваемого
величинам
 и
и
 ,
может описывать распределение тепла в
среде с источниками, распределение
потенциала электростатического поля
в электростатике.
,
может описывать распределение тепла в
среде с источниками, распределение
потенциала электростатического поля
в электростатике.
2. Постановка краевой задачи поперечных колебаний тонкой струны.
Рассмотрим процесс колебаний тонкой
струны длины
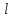 .
В момент времени
.
В момент времени
 точкам струны сообщают начальные
отклонения и скорости.
точкам струны сообщают начальные
отклонения и скорости.
Поставим задачу для определения малых
поперечных колебаний точек струны при
 ,
если:
,
если:
а) концы струны жестко закреплены;
б) концы струны свободны;
в) концы струны закреплены упруго;
г) концы струны движутся в поперечном направлении по заданному закону.
Рассмотрим процесс колебаний тонкой упругой нити, которая может свободно изменять свою форму. Тогда напряжения, возникающие в упругой нити, направлены по касательной к ее мгновенному профилю, такую нить будем называть струной.
Пусть в положении равновесия струна расположена вдоль Оx. Будем рассматривать только поперечные колебания струны, считая, что перемещение частиц струны происходит в одной плоскости и все точки струны движутся перпендикулярно Оx.
Обозначим через
 отклонение от оси положения равновесия
точки струны с абсциссой х в момент
времени
отклонение от оси положения равновесия
точки струны с абсциссой х в момент
времени
 .
В момент t график
функции
.
В момент t график
функции
 в плоскости UX
представляет собой профиль струны.
Рассматриваем только малые колебания,
такие, что смещение
в плоскости UX
представляет собой профиль струны.
Рассматриваем только малые колебания,
такие, что смещение
 и производные
и производные
 столь малы, что квадратами этих
величин и их произведениями можно
пренебречь. Тогда
столь малы, что квадратами этих
величин и их произведениями можно
пренебречь. Тогда

По этой же причине не происходит удлинения участков струны.


В этом случае, согласно закону Гука, натяжение Т в каждой точке струны не будет изменяться. Покажем, что натяжение Т можно считать независящим от точки приложения х. Для поперечных колебаний струны сумма проекций на ось ОХ сил натяжения равна нулю:

Где
 - малые углы, следовательно
- малые углы, следовательно


В случае вынужденных
колебаний на струну действует внешняя
распределенная сила
 ,
направление которой будем считать
перпендикулярным оси Ох.
,
направление которой будем считать
перпендикулярным оси Ох.
Распределение масс в струне
будем характеризовать линейной
плотностью
 ,
которая в общем случае
изменяется вдоль струны. Для однородной
струны постоянного сечения
,
которая в общем случае
изменяется вдоль струны. Для однородной
струны постоянного сечения

Перейдем к построению математической модели. Используя 2 закон Ньютона

где
 - импульс системы,
равный сумме импульсов всех ее частиц;
F
– результирующая внешняя сила.
- импульс системы,
равный сумме импульсов всех ее частиц;
F
– результирующая внешняя сила.
В качестве такой механической
системы рассмотрим выделенный участок
струны
 ,
в нем
,
в нем
 .
Учитывая, что движение
этой системы происходит в направлении,
перпендикулярном оси Ох,
запишем уравнение
(1) в проекции на ось Ои:
.
Учитывая, что движение
этой системы происходит в направлении,
перпендикулярном оси Ох,
запишем уравнение
(1) в проекции на ось Ои:

Так как проекция суммарного импульса системы

то

Проекция внешних сил на направление Ou состоит из двух слагаемых. Одно из них учитывает действие сил натяжения на концах выделенного участка струны, а другое - суммарную вынуждающую силу, действующую на частицы этого участка струны. Эти проекции определяются следующими соотношениями:




В силу произвольности выбора
отрезка
 из (6) следует, что в любой точке струны
в любой момент времени
из (6) следует, что в любой точке струны
в любой момент времени
 подынтегральное
выражение =0, т.е.
подынтегральное
выражение =0, т.е.

Полученное соотношение
представляет собой Д.У. в частных
производных 2-го порядка относительно
искомой функции
 .
Оно описывает процесс малых поперечных
колебаний струны, и его называют
неоднородным одномерным волновым
уравнением (уравнением
плоских волн). Это уравнение гиперболического
типа.
.
Оно описывает процесс малых поперечных
колебаний струны, и его называют
неоднородным одномерным волновым
уравнением (уравнением
плоских волн). Это уравнение гиперболического
типа.
В случае постоянной линейной
плотности
 уравнение колебаний однородной струны
принимает вид
уравнение колебаний однородной струны
принимает вид

где
 ;
;

Если внешних сил нет, то
 ,
и однородное волновое уравнение имеет
вид:
,
и однородное волновое уравнение имеет
вид:


- трехмерное однородное уравнение.
Поставим начальные и граничные условия. Из постановки задачи следует, что начальные отклонения точек струны и начальные скорости известны:

 и
и
 - известные функции.
- известные функции.
Рассмотрим условия на границе струны.
а) Если концы струны жестко закреплены, то граничные условия принимают вид:

б)
Рассмотрим случай, когда концы струны
свободны. Выберем участок KM
на левой границе струны. Длина этого
участка
 ,
причем
,
причем
 .
.
При рассмотрении колебаний участка KM струну в его окрестности нельзя считать бесконечно тонкой. Поэтому помимо деформаций растяжения – сжатия следует учитывать деформацию изгиба. Натяжение струны вследствие изгиба
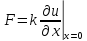
Поскольку струна является свободной,
последнее выражение необходимо приравнять
нулю, откуда следует 
Аналогично для
 запишем:
запишем:
 .
.
в) Если концы
струны закреплены упруго, то на них
действует сила упругости
 .
По закону Гука
.
По закону Гука 
Последнее равенство перепишем в виде:


где
 .
.
г) Если концы струны движутся в поперечном направлении по заданному закону, то граничные условия имеют вид:

Здесь
 и
и
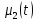 – известные функции времени. В силу
непротиворечивости постановки
начально-краевой задачи функции
– известные функции времени. В силу
непротиворечивости постановки
начально-краевой задачи функции
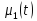 и
и
 должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:

Итак, малые поперечные колебания струны описываются уравнением (7), (8), (9) с начальными условиями (10) и парой граничных условий вида (11)-(15).
