
- •Раздел 1
- •Раздел 2
- •Примеры
- •1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
- •2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
- •15 Вопрос Задача о касательной
- •18 Вопрос Производная сложной функции
- •19 Вопрос Производная обратной функции
- •21 Вопрос
- •25 Вопрос Общая схема исследования функции и построения ее графика.
- •29 Вопрос
- •38 Вопрос Свойства определенного интеграла
Раздел 1
1 вопрос- Математика – наука о количественных отношениях и пространственных формах действительного мира. Академик А.Н. Колмогоров выделяет 4 этапа развития матем-ки: зарождение мат-ки; элементарной мат-ки; матем-ки переменных величин; современной матем-ки. Понимание самостоятельного положения матем-ки как особой науки стало возможным после накопления достаточно большого фактического материала и возникло впервые в Древней Греции в 6-5 веке до н.э. Это было началом периода элементарной матем-ки. В теч. Этого периода матем-кие исследования имеют дело лишь с достаточно ограниченным запасом основных понятий, возникших в связи с самыми простыми запросами хоз. жизни. Из арифметики постепенно вырастает теория чисел. Создается алгебра как буквенное исчисление. В 17 веке запросы естествознания и техники привели к созданию методов, позволяющих математически изучать движение, процессы изменения величин, преобразование геометрических фигур. С употребления переменных величин в аналитической геометрии и создания дифференциального и интегрального исчисления начинается период матем-ки переменных величин. На первый план выдвигается понятие функции. Изучение функции приводит к основным понятиям матем-го анализа: пределу, производной, дифференциалу, интегралу. Создание аналитической геометрии позволило расширить предмет изучения геометрии благодаря найденному методу координат Р.Декарта. С другой стороны открылась возможность геометрической интерпретации алгебраических и аналитических фактов. Дальнейшее развитие привело в начале 19 века к постановке задачи изучения возможных типов количественных отношений и пространственных форм с достаточно общей точкой зрения. Новые теории возникают также вследствие внутренней потребности самой матем-ки. Примером такой теории является «воображаемая» геометрия Н.Лобачевского. Развитите подобного рода исследований в матем-ке 19-20 вв позволяет отнести ее к периоду современной матем-ки.
2 вопрос- Множество – совокупность некоторых объектов. Примерами множеств являются множества чисел, множества точек прямой, множество линий и др. Каждое отдельное множество задается правилом или законом, позволяющим судить, принадлежит объект данному множеству или нет.
Множества обозначаются прописными буквами латинского или готического алфавита: A, B, ...,M, K,... . Если множество A состоит из элементов a,b,c,..., это обозначается с помощью фигурных скобок: A={a,b,c,...,} . Если a есть элемент множества A , то это записывают следующим образом: a A. Если же a не является элементом множества A , то пишут a A. Одним из важных множеств является множество N всех натуральных чисел N={1,2,3,...,} . Существует также специальное, так называемое пустое множество, которое не содержит ни одного элемента. Пустое множество обозначается символом .
Примеры множеств:
1) множество точек данной геометрической фигуры;
2) множество чётных чисел;
3) множество корней уравнения х2-5х+6=0;
4) множество действительных корней уравнения х2+9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». Объекты, составляющие данное множество, называют его элементами. С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множества
Основные операции:
-
Принадлежность элемента множеству:
![]()
где
![]() --
элемент и
--
элемент и
![]() --
множество (элемент
--
множество (элемент
![]() принадлежит
множеству
принадлежит
множеству ![]() ).
).
-
Непринадлежность элемента множеству:
![]()
где
![]() --
элемент и
--
элемент и
![]() --
множество (элемент
--
множество (элемент
![]() не
принадлежит множеству
не
принадлежит множеству ![]() ).
).
-
Объединение множеств:
 .
.
Объединением
двух множеств
![]() и
и
![]() называется
множество
называется
множество
![]() ,
которое состоит из элементов множеств
,
которое состоит из элементов множеств
![]() и
и
![]() ,
т.е.
,
т.е.
![]() или
или![]()
-
Пересечение множеств:
 .
.
Пересечением
двух множеств
![]() и
и
![]() называется
множество
называется
множество
![]() ,
которое состоит из общих элементов
множеств
,
которое состоит из общих элементов
множеств
![]() и
и
![]() ,
т.е.
,
т.е.
![]() и
и![]()
-
Разность множеств:
 .
.
Разностью
двух множеств
![]() и
и
![]() ,
например, множество
,
например, множество
![]() минус
множество
минус
множество
![]() ,
называется множество
,
называется множество
![]() ,
которое состоит из элементов множества
,
которое состоит из элементов множества
![]() ,
которых нет в множестве
,
которых нет в множестве
![]() ,
т.е.
,
т.е.
![]() и
и![]()
-
Симметрическая разность множеств:
 .
.
Симметрической
разностью двух множеств
![]() и
и
![]() называется
множество
называется
множество
![]() ,
которое состоит из не общих элементов
множеств
,
которое состоит из не общих элементов
множеств
![]() и
и
![]() ,
т.е.
,
т.е.
![]()
-
Дополнение множества:
 .
.
Если
предположим, что множество
![]() является
подмножеством некоторого универсального
множества
является
подмножеством некоторого универсального
множества
![]() ,
тогда определяется операция дополнения:
,
тогда определяется операция дополнения:
![]() и
и![]()
7.Вхождение
одного множества в другое множество:
![]() .
.
Если
любой элемент множества
![]() является
элементом множества
является
элементом множества
![]() ,
то говорят, что множество
,
то говорят, что множество
![]() есть
подмножество множества
есть
подмножество множества
![]() (множество
(множество
![]() входит
в множество
входит
в множество
![]() ).
).
-
Не вхождение одного множества в другое множество:
 .
.
Если
существует элемент множества
![]() ,
который не является элементом множества
,
который не является элементом множества
![]() ,
то говорят, что множество
,
то говорят, что множество
![]() не
подмножество множества
не
подмножество множества
![]() (множество
(множество
![]() не
входит в множество
не
входит в множество
![]() ).
).
3 вопрос- Матрицей размер m*n назыв-ся прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, назыв-ся элементами матрицы. Матрицы обозначаются прописными буквами латинского алфавита, например, А, В, С…, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: аij, где i-номер строки, j- номер столбца. Две матрицы одного размера называются равными, если они совпадают поэлементно, т.е. аij=bij для любых i=1,2,.., m; j=1,2,…n. Матрица из одной строки называется матрицей (вектором)-строкой, а из 1 столбца – матрицей (вектором)-столбцом. Матрица наз-ся квадратной n-го порядка, если число строк равно числу столбцов и равно n. Элементы матрицы, у которой номер столбца равно номеру строки, назыв-ся диагональными и образуют главную диагональ матрицы. Если у диагональной матрицы все диагональные элементы равны, то матрица назыв-ся единичной.
Матрицы специального вида
Квадратная
матрица
![]() называется
верхней
треугольной,
если
называется
верхней
треугольной,
если
![]() при
i>j,
и нижней
треугольной,
если
при
i>j,
и нижней
треугольной,
если
![]() при
i.
при
i.
Общий вид треугольных матриц:

Заметим,
что среди диагональных элементов
![]() могут
быть равные нулю элементы. Матрица
могут
быть равные нулю элементы. Матрица
![]() называется
верхней
трапециевидной,
если выполнены следующие три условия:
называется
верхней
трапециевидной,
если выполнены следующие три условия:
1.
![]() при
i>j;
при
i>j;
2.
Существует такое натуральное число r,
удовлетворяющее неравенствам
![]() ,
что
,
что
![]() .
.
3.
Если какой-либо диагональный элемент
![]() ,
то все элементы i-й
строки и всех последующих строк равны
нулю.
,
то все элементы i-й
строки и всех последующих строк равны
нулю.
4 вопрос- Над матрицами можно производить ряд операций. 1. Умножение матриц на число – произведением матрицы А на число λ назывется матрица В=λА, элементы которой bij=aij, для i=1,2,…m; j=1,2,...n. В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е. 0*А=0 2. Сложение матриц – суммой 2-х матриц А и В одинакового размера наз-ся матрица С=А+В (складывается поэлементно). В частном случае А+0=А. 3. Вычитание матриц – разность 2-х матриц одинакового размера определяется через предыдущие операции А-В=А+(-1)*В 4. Умножение матриц- умножение матрицы А на матрицу В определено, когда число столбцов 1 матрицы равно числу строк 2 матрицы. Тогда произведением матриц А на В называется такая матрицы С, каждый элемент которой равен сумм произведений элементов строки матрицы А на соответствующие элементы столбца матрицы В. 5. Возведение в степень – целой положительной степенью Аm (m>1) квадратной матрицы А назыв-ся произведение m матриц, равных А. Данная операция определяется только для квадратных матриц. 6. Транспонирование матриц – переход от матрицы А к матрице А҆ , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А҆ назыв-ся транспонированной относительно А.
5 вопрос Свойства определителей матриц:
Свойство № 1:
Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т
Следствие:
Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.
Свойство № 2:
При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:
Свойство № 3:
Определитель матрицы, имеющий два одинаковых ряда, равен нулю.
Свойство № 4:
Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.
Следствия из свойств № 3 и № 4:
Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5:
Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.
Свойство № 6:
Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:
Свойство № 7:
Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.
6 вопрос Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
 .
Произведения
.
Произведения
 называются членами определителя 2-го
порядка.
называются членами определителя 2-го
порядка.
Пример.
Вычислить
определитель матрицы
 .
Р е ш е н и е.
.
Р е ш е н и е.
 .
.
7 вопрос Определителем матрицы третьего порядка или определителем третьего порядка, называется число, которое вычисляется по формуле: ∆3=|A|= а11а 22 а33+ а12а 23а 31+ а21а32 а13- а31а 22а 13-а12 а21 а33-а32 а23 а11 Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы
9
вопрос Матрица
А-1
называется обртаной по отношению к
квадратной матрице А, если при умножении
этой матрицы на данную как справа, так
и слева получается единичная матрица.
Алгоритм
вычисления обратной матрицы: 1.
Находим определитель исходной матрицы.
Если |А|=0, то матрица А-вырожденная и
обратной матрицы А-1
не существует. Если |А|не равно 0, то
матрица А-невырожденная и обратная
матрица существует. 2. Находим матрицу,
транспонированную к А. 3. Находим
алгебраические дополнения элементов
транспонированной матрицы и составляем
из них присоединенную матрицу 4. Вычисляем
обратную матрицу по формуле 5. Проверяем
правильность вычисления обратной
матрицы. Обратная
матрица существует (и единственна) тогда и только
тогда, когда исходная матрица является
невырожденной (неособенной) и вычисляется
по формуле
существует (и единственна) тогда и только
тогда, когда исходная матрица является
невырожденной (неособенной) и вычисляется
по формуле ,
,
11 вопрос - Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Обычно
ранг матрицы A
обозначается
![]() (
(![]() )
или
)
или
![]() .
Оба обозначения пришли к нам из иностранных
языков, потому и употребляться могут
оба.
.
Оба обозначения пришли к нам из иностранных
языков, потому и употребляться могут
оба.
12 вопрос Совокупность уравнений

относительна неизвестных x1, x2, ..., xn-1, xn называется системой линейных алгебраических уравнений.
Числа aij — коэффициенты системы, bi— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.
Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.
Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.
Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.
Если среди правых частей bi системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.
Если все правые части системы равны нулю, то система называется однородной.
Система
линейных уравнений может быть записана
в матричной форме A·x = b:

Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
A(1)x1 + A(2)x2 +…+ A(n)xn = b. Здесь A(1), A(2), ... , A(n) — столбцы матрицы системы.

Матрица Ap называется расширенной матрицей системы.
Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.
13 вопрос Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних по номеру переменных, находятся остальные переменные. Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду Ux=c, На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1, после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д.
Пусть исходная система выглядит следующим образом

Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При
этом будем считать, что базисный
минор (ненулевой минор максимального
порядка) основной матрицы находится в
верхнем левом углу, то есть в него входят
только коэффициенты при переменных ![]() [3].
[3].
Тогда
переменные ![]() называются главными
переменными.
Все остальные называются свободными.
называются главными
переменными.
Все остальные называются свободными.
Если
хотя бы одно число ![]() ,
где i > r,
то рассматриваемая система несовместна.
,
где i > r,
то рассматриваемая система несовместна.
Пусть ![]() для
любых i > r.
для
любых i > r.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом ![]() (
(![]() ,
где
,
где ![]() —
номер строки):
—
номер строки):
 ,
где
,
где ![]()
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
14 вопрос Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Для множества М решений системы имеются три возможности:
1) M = Æ (в этом случае система несовместна);
2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);
3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.
Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (m³n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2,
an1 x1 + an1 x2 +... + ann xn = bn.
Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных;2)поформуламКрамера;3) матричным методом
15
вопрос Также
как и матричный метод, этот метод
применятся для решения систем линейных
уравнений, в которых число уравнений
 и число неизвестных
и число неизвестных
 совпадают и матрица
совпадают и матрица
 системы – невырожденная. Справедлива
следующая теорема.
системы – невырожденная. Справедлива
следующая теорема.
ТЕОРЕМА
(Крамера). Если в системе линейных
уравнений число уравнений
 и число неизвестных
и число неизвестных
 совпадает и
совпадает и
 ,
то система совместна и имеет единственное
решение, которое может быть найдено по
формулам
,
то система совместна и имеет единственное
решение, которое может быть найдено по
формулам
 (
( ),
),
где
 ,
а
,
а
 – определитель, получаемый из определителя
– определитель, получаемый из определителя
 заменой его
заменой его
 -го
столбца на столбец свободных членов.
-го
столбца на столбец свободных членов.
Формулы называются формулами Крамера.
16 вопрос Изучение балансовых моделей, представляющих собой одно из важнейших направлений и экономико-математических исследований, должно служить объектом изучения отдельной дисциплины. Цель балансового анализа –ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой, как потребитель и своей, и произведенной другими отраслями. Связь между отраслями отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936г экономистом Леонтьевым В. Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска Х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y. Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отрасли и другими отраслями, а др. часть предназначена для целей конечного личного и общественного потребления. Можно полагать, что в некотором промежутке времени коэффициенте будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.
17 вопрос Матрица А≥0 называется продуктивной, если для любого вектора Y≥0 существует решение Х≥0. В этом случае и модель Леонтьева называется продуктивной. Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше 1, т.е. матрица А продуктивна, если аij≥0 для любых i,j=1,2,…n. Матрицу (E - A)-1 называют матрицей полных затрат.
18
вопрос
Вектором
называется направленный отрезок АВ с
начальной точкой А и конечной точкой В
(который можно перемещать параллельно
самому себе). Векторы могут обозначаться
как 2 прописными буквами, так и одной
строчной с чертой или стрелкой. Длинной
(или модулем) вектора называется число,
равное длине отрезка, изображающего
вектор. Векторы, лежащие на одной прямой
или на параллельных прямых, наз-ся
коллинеарными. Если начало и конец
вектора совпадают, такой вектор наз-ся
нулевым. Произведением
вектора на число
 :
будет вектор,
:
будет вектор,
 имеющий
длину
имеющий
длину , направление которого совпадает с
направлением вектора
, направление которого совпадает с
направлением вектора
 ,
если
,
если
 ,
и противоположно ему, если
,
и противоположно ему, если
 .Противоположным
вектором -
.Противоположным
вектором - называется произведение вектора -
называется произведение вектора - на число (-1), т.е. -
на число (-1), т.е. - =
= .
Суммой двух векторов
.
Суммой двух векторов
 и
и
 называется
вектор
называется
вектор
 ,
начало которого совпадает с началом
вектора
,
начало которого совпадает с началом
вектора
 ,
а конец с концом вектора
,
а конец с концом вектора
 ,
при условии, что начало
,
при условии, что начало
 совпадает с концом
совпадает с концом
 .
(правило треугольников). Аналогично
определяется сумма нескольких векторов.
Разностью двух векторов
.
(правило треугольников). Аналогично
определяется сумма нескольких векторов.
Разностью двух векторов
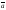 и
и
 называется
сумма вектора
называется
сумма вектора
 и вектора -
и вектора - ,
противоположного
,
противоположного
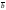 .
.
19
вопрос :
Скалярным произведение
 двух
векторов
двух
векторов
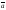 и
и
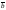 называется число, равное произведению
длин этих векторов на косинус угла
называется число, равное произведению
длин этих векторов на косинус угла
 между
ними:
между
ними:
 .
Свойства
скалярного произведения. Для
любых векторов a , b , c и
любого числа m справедливы
следующие соотношения:
.
Свойства
скалярного произведения. Для
любых векторов a , b , c и
любого числа m справедливы
следующие соотношения:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
20 вопрос комплексными числами называются выражения вида
 ,
,
где
 и
и
 – действительные числа, а
– действительные числа, а
 – некоторый символ, удовлетворяющий
условию
– некоторый символ, удовлетворяющий
условию
 .
Число
.
Число
 называется действительной частью
комплексного числа
называется действительной частью
комплексного числа
 ,
а число
,
а число
 – его мнимой частью. Для их обозначения
используются символы
– его мнимой частью. Для их обозначения
используются символы
 ,
,
 .
.
Комплексные
числа вида
 являются действительными числами и,
следовательно, множество комплексных
чисел содержит в себе множество
действительных чисел.
являются действительными числами и,
следовательно, множество комплексных
чисел содержит в себе множество
действительных чисел.
Комплексные
числа вида
 называются чисто мнимыми. Два комплексных
числа вида
называются чисто мнимыми. Два комплексных
числа вида
 и
и
 называются равными, если равны их
действительные и мнимые части, т.е. если
выполняются равенства
называются равными, если равны их
действительные и мнимые части, т.е. если
выполняются равенства
 ,
,
 .
.
21 вопрос Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.
Суммой
двух комплексных чисел
 и
и
 называется комплексное число
называется комплексное число
 вида
вида
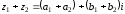 .
.
Произведением
двух комплексных чисел
 и
и
 называется комплексное число
называется комплексное число
 вида
вида
 .
.
-
Коммутативный (переместительный) закон сложения:
 .
.
-
Ассоциативный (сочетательный) закон сложения:
 .
.
-
Коммутативный закон умножения:
 .
.
-
Ассоциативный закон умножения:
 .
.
-
Дистрибутивный (распределительный) закон умножения относительно сложения:
 .
.
6.
 .
.
7.
 .
.
8.
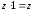 .
.
9.
Любому комплексному числу
 соответствует противоположное комплексное
число
соответствует противоположное комплексное
число
 такое, что
такое, что
 .
.
10.
Всякому комплексному числу
 отличному от нуля, соответствует обратное
комплексное число
отличному от нуля, соответствует обратное
комплексное число
 такое, что
такое, что
 .
.
22
вопрос Комплексное
число
 называется сопряженным комплексному
числу
называется сопряженным комплексному
числу
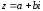 ,
если
,
если
 .
.
23 вопрос Запись отличного от нуля комплексного числа z в виде
 (2)
(2)
называется тригонометрической формой комплексного числа z. Число r называется модулем комплексного числа z, а число φ называется аргументом этого комплексного числа и обозначается Arg z.
Тригонометрическая форма записи комплексного числа – (формула Эйлера) – показательная форма записи комплексного числа:
 .
.
У комплексного числа z имеется бесконечно много аргументов: если φ0 – какой-либо аргумент числа z, то все остальные можно найти по формуле
 .
.
Для
комплексного числа
 аргумент и тригонометрическая форма
не определяются.
аргумент и тригонометрическая форма
не определяются.
Формулы умножения и деления комплексных чисел в тригонометрической форме имеют следующий вид:
 .
.
 .
.
24
вопрос Извлечение
квадратного корня из комплексного числа
 .
Пусть
.
Пусть
 ,
,
где x и y – действительные числа. Возводя обе части этого равенства в квадрат, получаем
 .
.
Что равносильно системе

Решая эту систему, получаем:
 ;
;
 .
.
Таким образом, извлечение корня квадратного из комплексного числа осуществляется по формуле
 .
.
В
скобках перед мнимой единицей берется
знак плюс, если
 ,
и знак минус, если
,
и знак минус, если
 .
.
При возведении в натуральную степень комплексного числа используется формула Муавра:
 .
(8)
.
(8)
При извлечении корня из комплексного числа используется формула:
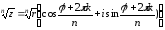 ,
(9)
,
(9)
где k=0, 1, 2, …, n-1.
25 вопрос Степени мнимой единицы.


Если
натуральный показатель степени m
при делении на 4 дает в остатке r,
т.е. если
 ,
где n
– натуральное число, то
,
где n
– натуральное число, то
 ;
;
при
этом

26 вопрос Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из Xв Y.
Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.
Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.
Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:
A(u + v) = A(u ) + A(v) , A(α·u) = α· A(u). Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {aij}= {A(ej )i}
27
вопрос .
Вектор
 называется
собственным
вектором
линейного оператора
называется
собственным
вектором
линейного оператора
 ,
если найдется такое число
,
если найдется такое число
 ,
что:
,
что:
Число
λ называется собственным
значением оператора A,
если существует такой ненулевой вектор x,
что справедливо равенство A(x)
= λ·x.
Любой ненулевой вектор x ≠0,
удовлетворяющий этому уравнению,
называетсясобственным
вектором оператора A,
отвечающим собственному значению λ.
Можно записать
в матричной форме: ,
где
,
где
 -
матрица-столбец из координат вектора
-
матрица-столбец из координат вектора
 .
Характеристическим
многочленом оператора
.
Характеристическим
многочленом оператора ![]() называется многочлен
называется многочлен ![]() .Характеристический
многочлен линейного оператора
.Характеристический
многочлен линейного оператора ![]() не
зависит от выбора базиса, в котором
представленаегоматрица.Уравнение
не
зависит от выбора базиса, в котором
представленаегоматрица.Уравнение ![]() называется характеристическим
уравнением оператора
называется характеристическим
уравнением оператора ![]() .
.
28 вопрос Теорема Фробениуса — Перрона (англ.):
Пусть A — квадратная матрица, со строго положительными вещественными элементами, тогда справедливы утверждения:
-
наибольшее по модулю собственное число является вещественным и строго положительным;
-
это собственное значение является простым корнем характеристического многочлена;
-
соответствующий собственной вектор имеет строго положительные координаты;
-
собственное значение удовлетворяет неравенствам.
![]()
29 вопрос Стандартная модель, также как и классические теории международной торговли, исходит из того, что мировая экономика представлена двумя странами, в каждой из которых производятся два товара: Х и Y.Кроме того, в стандартной модели используются следующие допущения: покупатели в процессе потребления стремятся обеспечить максимум эффекта (графически это изображается с помощью кривых безразличия), а производители стремятся извлечь максимум прибыли; на внутреннем и мировом рынках существует совершенная конкуренция, в условиях которой равновесная цена устанавливается на уровне, соответствующем предельным издержкам производства. Таким образом, для рассматриваемой страны рост цен на экспортируемые товары по отношению к импортируемым (Px/Ру) приведет к повышению ее благосостояния, а понижение цен, наоборот, - к уменьшению его. Если же цены на импортируемые товары (в нашем случае Ру) будут расти, то это будет означать снижение благосостояния страны.
Подобная логика лежит в основе расчета условий торговли, т.е. показателя, равного частному от деления цены экспортируемого товара (товаров) на цену импортируемого товара (товаров).
30
вопрос Деление
отрезка в данном отношении. Требуется
разделить отрезок АВ, соединяющий
точки А(х1;у1)и B(x2;y2) в
заданном отношении l >
0, т.е. найти координаты точки М(х;у)
отрезка АВ такой,
что ![]() Решение:
Введем в рассмотрение векторы
Решение:
Введем в рассмотрение векторы ![]() и
и ![]() . Точка М делит
отрезок АВ в
отношении l,
если
. Точка М делит
отрезок АВ в
отношении l,
если![]() .
.
Но ![]() т.е.
т.е. ![]() и
и ![]() т.е.
т.е. ![]() Уравнение
(1) принимает вид
Уравнение
(1) принимает вид
![]()
Учитывая,
что равные векторы имеют равные
координаты, получаем![]() т.е.
т.е. ![]()
![]() т.е.
т.е. ![]()
Формулы
называются формулами
деления отрезка в данном отношении. В
частности, при l=1, т.е.
если АМ=МВ, то они примут вид ![]() ,
, ![]() .
В этом случае точка М(х;
у) является серединой
отрезка АВ.
.
В этом случае точка М(х;
у) является серединой
отрезка АВ.
Замечание: Если l =
0, то это означает, что точки А и М совпадают,
если l <
0, то точка М лежит
вне отрезка АВ
— говорят,
что точка М делит
отрезок АВ внешним
образом (l¹ -1
, т. к. в противном случае ![]() т.
е. AM + MB =
0, т. е. АВ =
0).
т.
е. AM + MB =
0, т. е. АВ =
0).
Площадь треугольника
Требуется найти площадь треугольника АВС с вершинами А(х1;у1),В(х2; y2), С(х3;у3).
Решение:
Опустим из вершин А,
В, С перпендикуляры АА1, BB1,
CC1 на
ось Ох (см.
рис. 5).
Очевидно, что ![]() .
.

Замечание: Если при вычислении площади треугольника получим S = 0, то это означает, что точки А, В, С лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.
31
вопрос Уравнение ![]() называется
уравнением прямой с угловым коэффициентом;
k - угловой коэффициент, b - величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
называется
уравнением прямой с угловым коэффициентом;
k - угловой коэффициент, b - величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
Если
прямая задана общим уравнением![]() ,
то ее угловой коэффициент определяется
по формуле
,
то ее угловой коэффициент определяется
по формуле![]() .
.
32 вопрос Пусть прямая проходит через точку М1(х1,у1) образует с осью Ох угол ᾲ≠ П/2. Так как точка М1 лежит на прямой, то ее координаты удовлетворяют уравнению у1=kx+b. Вычитывая равенство 1 из равенства 2, получим уравнение искомой прямой у-у1=k(x-x1)
33
вопрос Пусть
в пространстве заданы две точки M1(x1, y1)
и M2(x2, y2)
и х1≠х2, у1≠у2. Для составления уравнения
прямой М1М2 запишем уравнение прямых,
проходящих через точку М1: у-у1=к(х-х1).
Т.к. точка М2 лежит на данной прямой, то
чтобы выделить ее из пучка, подставим
координаты точки М2 в уравнение пучка
у2-у1=к(х2-х1) и найдем угловой коэффициент
прямой
 . Теперь уравнение искомой прямой примет
вид
. Теперь уравнение искомой прямой примет
вид
 =
=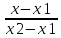
34 вопрос Углом между пересекающимися прямыми на плоскости, называется градусная мера наименьшего из углов, образованных при пересечении этих прямых. Угол между совпадающими или параллельными прямыми считается равным нулю. Угол α между двумя прямыми, заданными уравнениями: y=k1x+b1 (первая прямая) и y=k2x+b2 (вторая прямая), может быть вычислен по формуле (угол отсчитывается от 1й прямой ко 2й против часовой стрелки): tg(α)=(k2-k1)/(1+k1k2). Условия параллельности двух прямых: а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:k1 = k2. б) Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.3.Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
36
вопрос
Рассмотрим
уравнение прямой с угловым коэффициентом
 .
Перенесем все слагаемые в левую часть
и перепишем его в следующем виде:
.
Перенесем все слагаемые в левую часть
и перепишем его в следующем виде:
 ,
,
 -
общее
уравнение прямой,
где
-
общее
уравнение прямой,
где
 и
и
 не
равны нулю одновременно, т.е.
не
равны нулю одновременно, т.е.
 .
.
Условия параллельности и перпендикулярности двух прямых:
Если
прямые
 и
и
 параллельны,
то угол
параллельны,
то угол
 и
и
 ,
откуда из формулы угла между двумя
прямыми
,
откуда из формулы угла между двумя
прямыми

 .
И наоборот, если
.
И наоборот, если
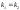 ,
то по этой же формуле
,
то по этой же формуле
 и
и
 .
.
Т.о., равенство угловых коэффициентов является необходимым и достаточным условием параллельности 2х прямых.
 -
условие
параллельности двух прямых.
-
условие
параллельности двух прямых.
Если
прямые перпендикулярны,
то
 ,
при этом
,
при этом
 или
или
 ,
откуда
,
откуда
 или
или
 .
.
Справедливо так же и обратное утверждение.
Т.о., для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
 -
условие
перпендикулярности двух прямых.
-
условие
перпендикулярности двух прямых.
Если
две прямые заданы уравнениями в общем
виде:
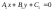 и
и
 ,
то учитывая
их угловые коэффициенты
,
то учитывая
их угловые коэффициенты
 и
и
 ,
условие параллельности прямых имеет
вид:
,
условие параллельности прямых имеет
вид:
 .
.
Следовательно, условием параллельности прямых, заданных общими уравнениями является пропорциональность коэффициентов при переменных.
Условие
перпендикулярности прямых
 в этом случае примет вид
в этом случае примет вид
 или
или
 ,
,
Т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.
37
вопрос
Пусть
даны точка М(х0,у0) и прямая Ах+Ву+С=0. Под
расстоянием от точки М до прямой АВ
понимается длина перпендикуляра d
=MN,
опущенного из точки М на прямую АВ. Для
определения расстояния d
необходимо: -составить уравнение прямой
MN,
перпендикулярной данной и проходящей
через точку М0(х0,у0) –найти точку N
(х1,у1) пересечения прямых, решив систему
уравнений этих прямых; - по формуле
определить расстояние между двумя
точками, т.е. найти d=MN.
В результате преобразованной получим

38 вопрос
Э́ллипс — геометрическое
место точек M Евклидовой
плоскости,
для которых сумма расстояний до двух
данных точек F1 и F2(называемых фокусами)
постоянна и больше расстояния между
фокусами, то есть | F1M |
+ | F2M |
= 2a, причем | F1F2 |
< 2a.
В
канонической для эллипса
системе координат уравнение
эллипса имеет вид ![]() . Оно
описывает эллипс с центром в начале
координат, оси которого совпадают с
осями координат.
. Оно
описывает эллипс с центром в начале
координат, оси которого совпадают с
осями координат.
39
вопрос
Гиперболой
называется геометрическое место точек,
для которых разность расстояний до двух
фиксированных точек плоскости, называеых
фокусами, есть постоянная величина;
указанная разность берется по абсолютному
значению и обозначается через2а. Фокусы
гиперболы обозначают буквами ![]() и
и ![]() ,
расстояние между ними - через 2с. По
определению гиперболы
,
расстояние между ними - через 2с. По
определению гиперболы ![]() ,
или
,
или ![]() .
.
Пусть
дана гипербола. Если оси декатовой
прямоугольной системы координат выбраны
так, что фокусы данной гиперболы
располагаются на оси абсцисс симметрично
относительно начала координат, то в
этой системе координат уравнение
гиперболы имеет вид
![]() ,
где
,
где ![]() .
Уравнение вида называется каноническим
уравнением гиперболы.
.
Уравнение вида называется каноническим
уравнением гиперболы.
Гипербола может быть определена несколькими путями. Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как скрещенные и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, скрещенные прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами. Гипербола может быть определена, как геометрическое место точек, разность расстояний которых до двух заданных точек, называемых фокусами, одинаково и равно 2a.Через директрису и фокус-геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная ε называется эксцентриситетом гиперболы.
40 вопрос Пара́бола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Каноническое
уравнение параболы в прямоугольной системе
координат:
![]() (или
(или ![]() ,
если поменять местами оси).
,
если поменять местами оси).
