Uch_posobie_MiR (typo vsya zachita)

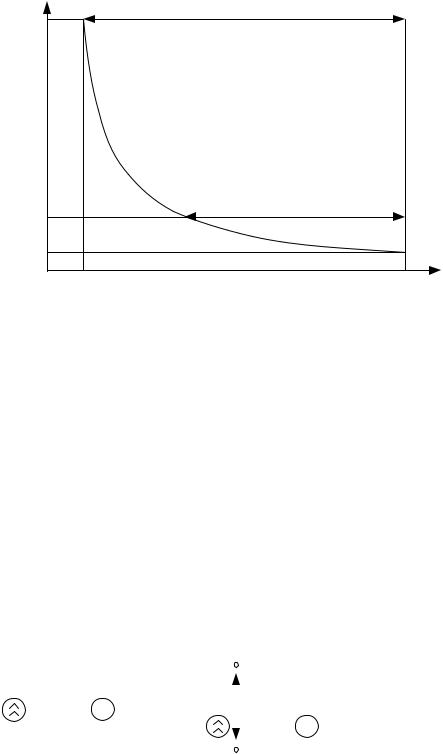
диапазона СИ. В начальной же части шкалы измерения недопустимы, в чём и заключается отрицательное влияние аддитивной погрешности, не позволяющее использовать один и тот же преобразователь для измерения как больших, так и малых измеряемых величин.

	(x) = D0/x	DП
100%
		DР
З
0		x
0	D0	L
Рис. 3. Относительная погрешность результата измерения

4. Систематические погрешности и их учёт.

Исключение систематических погрешностей – одна из главных задач при планировании, подготовке, проведении измерений и обработке их результатов.

Универсальных способов борьбы с систематическими погрешностями нет. Наиболее характерные ситуации, встречающиеся на практике.

1.Установка нуля, предварительная калибровка – реальные условия изме-

рений позволяют устранить источник погрешностей до начала измерений.

2.Метод теоретического анализа – сводится к усложнению модели за счёт учёта ранее неучтенных факторов. Например, наличие сопротивления проводов, внутреннего сопротивления источника и т.п. (рис. 4). Таким образом, систематическую погрешность можно рассчитать на основании известных характеристик используемых приборов или особенностей метода измерения, т.е. по формулам.

R

I

E

R

UВЫХ = E – IRi

R

U вых

E

Ri

UВЫХ

RА

I

А

R R A

E

А

Рис. 4. Применение метода теоретического анализа

11

3.Метод введения поправок и поправочных множителей – если происхож-

дение погрешности известно и её значение (абсолютная величина и знак) достаточно точно определены. Поправка – это значение физической величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению для исключения систематической погрешности (поправка численно равна абсолютной систематической погрешности, но имеет обратный знак). Поправочный множитель – число, на которое с той же целью умножают результат измерения.

4.Метод замещения – измеряемую величину замещают мерой и по разнице показаний прибора и значением меры определяют поправку (рис. 5). Если такой меры нет, то метод не применим.

	Rx	RЭ		Магазин
				сопротивлений

W

W

Рис. 5. Применение метода замещения

5. Метод компенсации погрешности по знаку – измерение проводят два-

жды так, чтобы известная по природе, но неизвестная по размеру погрешность входила в результаты измерений с противоположными знаками. Погрешность исключается при вычислении среднего значения.

Данный способ широко используется для исключения погрешности связанной с влиянием магнитного поля Земли (рис. 6). Первое измерение можно проводить, когда СИ находится в произвольном положении. Перед проведением второго измерения СИ поворачивают в горизонтальной плоскости на 180°. Если в первом случае магнитное поле Земли, складываясь магнитным полем прибора, вызывает погрешность с положительным знаком, то при повороте на 1800 магнитное поле Земли будет оказывать противоположное действие и вызовет погрешность равную по величине, но противоположного знак.

N S N S

Рис. 6. Исключение погрешности, связанной с влиянием магнитного поля Земли Одной из причин систематической погрешности в стрелочном приборе явля-

ется момент трения (рис. 7). К измеряемой величине подходят со стороны меньших и больших значений, и результат получают как полусумму этих значений.

12

МВР			A1
	МТР						A0
	МТР		МВР					A2
						A1 A2
			A
	0					2

Рис. 7. Исключение погрешности, связанной с моментом трения в стрелочном приборе

6.Метод образцовых сигналов – поочередно измеряют неизвестный и эталонный сигнал того же порядка. Поправку находят из показаний прибора по эталонному сигналу.

7.Поверка средств измерений – установление органом государственной метрологической службы (или другим официально уполномоченным органом, организацией) пригодности средства измерений к применению на основе экспериментально определенных метрологических характеристик и подтверждения их соответствия установленным обязательным требованиям. Основной метрологической характеристикой, определяемой при поверке СИ, является его погрешность. Она находится путём сравнений показаний поверяемого СИ и рабочего эталона.

8.Рандомизация – перевод систематической погрешности в случайную, путём измерения неизвестной величины несколькими приборами, и вычисления среднего значения по всем измерениям, принимаемого за оценку истинного значения. Метод применяется, когда причины систематической погрешности ясны из физических соображений, но её абсолютная величина и знак неизвестны, а имеются сведения лишь о пределах, в которых может, находится значение систематической погрешности.

9.Термостатирование и термоизоляция отдельных узлов или всего измерительного прибора, проведение измерений в термостатированных помещениях (для исключения температурной погрешности), применение экранов для защиты от влияния электромагнитных полей, использование стабилизированных источников питания, амортизация прибора, удаление его от источников возможного воздействия, от объектов измерений.

10.Проведение измерения несколькими различными методами, различными приборами при различных условиях, если о систематических погрешностях ничего неизвестно, хотя в действительности они имеются, и их значения существенны.

Смысл всех методов борьбы с систематической погрешностью сводится и нахождению поправки и использования её для уничтожения сист (поправка равна по величине и противоположна по знаку систематической погрешности).

13

5.Случайные погрешности.

Воснове методов исключения влияния случайных погрешностей лежат методы математической статистики, имеющие дело со случайными величинами. В теории измерений для описания погрешности измерений используют интегральные или дифференциальные функции распределения.

Под интегральной функцией распределения результатов измерений понимают вероятность того, что результат измерения А в i-м опыте окажется меньше некоторого текущего значения x, т.е. F(x) = Р{Ai ≤ x}.

Если рассматривать результат отдельного наблюдения Ai как случайную

точку на оси 0x (рис. 8), то значение интегральной функции распределения точки x' численно равно вероятности того, что случайная точка Ai в результате i-го измерения займет некоторое положение левее точки x'. Эти вероятности, очевидно, различны для различных точек x'. При перемещении точки x' вправо вдоль числовой оси, вероятность того, что в результате измерения точка Ai расположится левее x', не может уменьшиться. Следовательно, F(x) – функция неубывающая: F(–∞) = 0,

F(+∞) = 1.

0		Ai		x'

Рис. 8. Результат наблюдения Ai на оси 0x Пусть X2 X1 (рис. 9). Тогда:

P A X2 = A X1 либо X1 A X2 = P A X1 + P X1 A X2

или

P X1 A X2 = P A X2 – P A X1 P X1 A X2 = F(X2) – F(X1).

Рис. 9. Распределение случайных величин на оси Т.е. вероятность попадания случайной величины в заданный интервал опре-

деляется крутизной функции распределения на этом интервале и равна разности F(X2) – F(X1) (рис. 10). Крутизна функции характеризуется производной.

F(D)

	0		D
X1 P1 X2	X1 P2 X2	X1 P3 X2

P1 ≈ P3 ≈ 0; P2 → наиболее вероятное событие

Рис. 10. Интегральная функция распределения

14

Поэтому более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:

f (x) dF (x) . dx

Термин «плотность вероятности» становится понятным при рассмотрении изменения непрерывной случайной величины в достаточно узких границах от x до x + Dx. Тогда:

f (x) dF(x) F(x Dx) F (x)		или f (x)	P x A x Dx	.
dx	Dx		Dx

При малом Dx функция f(x) имеет смысл плотности вероятности, так как она равна отношению вероятности попадания случайной величины внутрь интервала (x, x + Dx) к длине этого интервала. Плотность вероятности, как производная неубывающей функции (интегральной функции распределения), не может принять отрицательных значений: f(x) 0.

При переходе от дифференциальной функции распределения к интегральной путём интегрирования получают:

x
F (x) f (x)dx	f (x)dx 1.

Т.е. площадь, заключенная между кривой дифференциальной функцией распределения и осью абсцисс, равна единице. При проведении измерения вероятность попадания результата измерения (рис. 11) в обозначениях дифференциальной функции распределения оценивается по формуле:

x2

P x1 A x2 f (x)dx .

x1

Таким образом, вероятность того, что значение непрерывной случайной величины находится внутри заданного интервала, равна площади под кривой распределения этой случайной величины на рассматриваемом интервале.

Рис. 11. Вероятность попадания результата измерения в заданный интервал

15

При этом закон распределения погрешностей измерения и закон распределения результатов измерений отличаются друг от друга на постоянную величину А – истинное значение измеряемой величины (рис. 12).

f(Dai)

f(ai)

A = const

Рис. 12. Распределение погрешности измерения ai и результата измерения ai Произведение f(x)dx называется элементом вероятности. Оно равно вероят-

ности того, что случайная величина x примет некоторое значение в интервале dх, поэтому по форме кривой распределения можно судить о том, какие интервалы значений измеряемой величины более, а какие менее вероятны.

Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают в основном при исследовании принципиально новых мер и измерительных приборов.

Значительно чаще бывает достаточно охарактеризовать случайные погрешности, с помощью ограниченного числа специальных величин, называемых моментами. Интеграл вида:

M [x] x f (x)dx ,

называется математическим ожиданием результатов наблюдений, принимаемого за оценку истинного значения измеряемой величины и являющуюся координатой центра тяжести фигуры образованной осью абсцисс и кривой распределения.

Опираясь на рассмотренное, можно дать более строгое определение постоянной систематической и случайной погрешностей.

Систематической погрешностью называется отклонение математического ожидания результатов наблюдений от истинного значения измеряемой величины:

сист = M[A] – A0.

Случайной погрешностью называют разность между результатом единичного наблюдения и математическим ожиданием результатов: случ = A – M[A].

В этих обозначениях истинное значение измеряемой величины составляет:

A0 = A – сист – случ.

16

Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений и обозначается D[x]:

D[x] M [(x M [x])2 ]	(x M [x])2 f (x)dx 2 f ( )d .

Дисперсия случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.

Действительно, как видно из формулы, дисперсия всё более увеличивается с ростом элементов вероятностей f( )d с появлением больших значений случайной погрешности, т.е. с увеличением рассеивания результатов наблюдений.

Реально каждой серии измерений, производимой с определенной группой измерительных приборов, соответствует свой закон распределения погрешностей. Установление и анализ этого закона существенно усложнили бы процедуру расчёта погрешностей измерения. Поэтому на практике обычно пользуются аппроксимацией реального закона распределения, сводя его к наиболее простому виду.

Нормальный закон распределения вероятности случайной составляющей погрешности наиболее часто встречается в природе и технике. Он является следствием одновременного действия большого числа независимых факторов, каждый из которых в отдельности незначительно влияет на результат измерения.

Для центральной случайной погрешности, имеющей нормальное распределение, плотность вероятности определяется выражением:

	f (D)					1			exp		D2
											2	2
					2 2
	или для результата измерений:
			1				(a M [x])2
	f (ai )						exp		i				,
											2	2
			2 2

где D[x] – среднеквадратическое отклонение имеет ту же размеренность, что и измеряемая величина; D[x] – имеет размерность квадрата измеряемой величины.

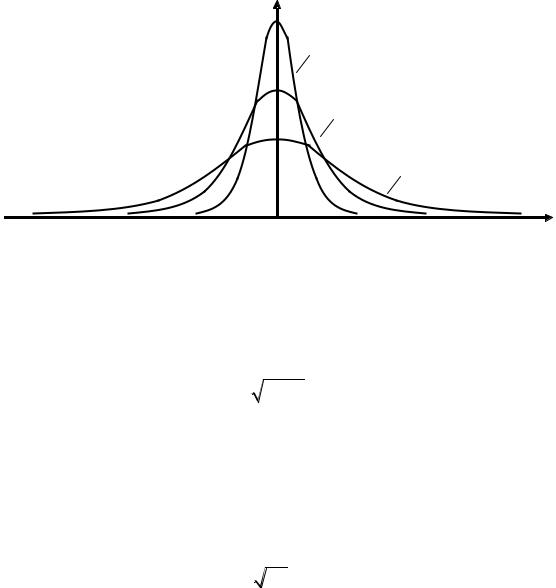
Кривые симметричные относительно оси Y, так как функция f(x) –чётная. Максимум кривых соответствует D = 0.

Из формулы следует, что распределение плотности вероятности при нормальном законе зависит от среднеквадратического отклонения (рис. 13). С увеличением максимальное значение f(x) уменьшается, кривая расширяется становится более пологой. Площадь, ограниченная графиком f(x) и осью абсцисс, остается при

17

этом неизменной, равной единице, таким образом					f (x)dx 1 при любых значе-
ниях среднеквадратического отклонения.
f(D)
	1					1 < 2 < 3
		2
						3
							D
0

Рис. 13. Распределение плотности вероятности от среднеквадратического отклонения

Вероятность того, что погрешность не превысит интервал D = – до D = + определяется соотношением:

		1					D2
P{ D }					exp		2	2	dD .	(1)
		2	2

Для проведения расчётов удобно связать величину со среднеквадратическим отклонением, т.е. принять: = k , где k – безразмерный коэффициент, – дисперсия. Тогда заменой переменной интеграл (1) приводится к известному интегралу вероятности, значения которого табулированы:

D = u предел = k k

			2		k		u2
	P{ k D k }				exp		2	du 2Ф(k) .	(2)
			2
				0

Это соотношение широко используется при практических расчётах. Из него следует, что: Р{–3 D 3 } = 2Ф(3) = 0,9973. Величину 3 принимают за максимальную погрешность при нормальном законе распределения.

J = 2 – доверительный интервал; Р – доверительная вероятность. Тогда результат измерения можно представить в виде:

A

где – точность, P – коэффициент доверия.

Таким образом, чтобы записать результат измерения необходимо знать А, и закон распределения. Но так как истинные значения А и неизвестны, то пользуются оценками этих величин.

18

В отличии от самих числовых характеристик оценки являются случайными величинами, причём их значения зависят от числа измерений, а распределение вероятностей – от закона распределения вероятности отдельного измерения.

Оценки должны удовлетворять трём условиям: быть состоятельными, несмещенными и эффективными.

Оценка называется состоятельной, если при увеличении числа опытов n оценка ȃ приближается к истинному значению a.

Оценка называется несмещенной, если математическое ожидание M[ȃ] = a. Очевидно, что если оценка несмещенная, то она не содержит систематической погрешности.

Оценка называется эффективной, если по сравнению с другими она обладает наименьшей дисперсией, т.е. D[ȃ] = min.

Запишем результат измерения в виде:

a1 = A + Da1, a2 = A + Da2, ... , an = A + Dan.

Суммируя почленно левые и правые части равенства получаем:

n						n
ai			nA Dai				,
i 1					i 1
откуда следует:
	1		n		1	n
A			ai			Dai .
	n i 1				n i 1

Если число наблюдений достаточно велико (строго говоря, n → ∞), то в силу нормального распределения, абсолютные погрешности одинаковой величины, но с различным знаком встречаются одинаково часто (плотность распределения симметрична относительно математического ожидания), а значит, второй член в пра-

вой части будет равен нулю: lim 1 n Dai 0 .

n n i 1

Таким образом при n → ∞ истинное значение измеренной величины равно среднему арифметическому:

An 1 n ai a . n i 1

На практике n ≠ ∞, т.е. чем меньше n, тем больше величина ȃ зависит от результатов отдельных наблюдений, но так как отдельные результаты наблюдений – случайные величины, то среднее арифметическое по конечному числу наблюдений

также будет случайной величиной.
Отклонение ȃ также случайная величина:
ȃ = A – ȃ	(3)

19

По смыслу ȃ – та погрешность, которую мы допускаем, взяв вместо истинного значения его оценку – среднее арифметическое ȃ. Эта погрешность, как было уже отмечено, тоже случайная и также описывается нормальным распределением с нулевым средним, но с другой дисперсией σ 2a :

			1			Da2
	f (Da)				exp	2	.
			2 a2
						2 a

Из (3) очевидно, что среднее ȃ также распределено по нормальному закону с той же дисперсией σ 2a . Выразим дисперсию σ 2a через дисперсию результатов наблюдений σ2.

Среднее есть линейная комбинация независимых случайных величин ai. Дисперсия линейной комбинация независимых случайных величия может быть выражена через дисперсию слагаемых:

D 1n n aii 1

1			n	1
			D[ai ]			nD[ai ], т. е.
n	2			n	2
			i 1
	2		2			(4)
	a		n

Таким образом дисперсия среднего по n наблюдений в n раз меньше дисперсии результата наблюдений, иными словами, если за результат измерения принять единичное наблюдение, то разброс такой оценки будет характеризоваться дисперсией σ2, а если усреднить результаты наблюдений и принять среднее по n наблюдения за оценку измеряемой величины, то дисперсия её будет σ 2a .

Теперь для определения доверительного интервала (ȃ – ε, ȃ + ε), в который попадает результат измерения с заданной вероятностью P, необходимо найти оценку дисперсии σ 2a .

Для нахождения оценки дисперсии можно воспользоваться методом максимального правдоподобия. Вероятность получить результат наблюдения в интервале ai ± 0,5Δi равна f(ai, A, )·Δi, где f(ai, A, ) – плотность распределения результатов наблюдений, зависящая от – дисперсии и A – истинного значения измеренной величины.

Так как результаты наблюдений независимы, то вероятность получить все n результатов в этом интервале равна:

n

P(a1, a2 ,..., an ; A; ) fi (ai , A, )Dai .

i 1

Смысл метода максимального правдоподобия заключается в том, что за оценку параметра распределения берут то его значение, при котором вероятность

20