Лекция 6 Исследование системы на модели в пространстве состояний

Устойчивость замкнутой системы

Используя правило вычисления обратной матрицы, из выражения (15) можно найти полином знаменателя W(p), равный det(pE-A), откуда находим

характеристическое уравнение:

det(pE-A)=0. (16)

В соответствии с необходимым и достаточным условием устойчивости замкнутой системы, получаем, что для устойчивости замкнутой системы требуется, чтобы уравнение det(pE–А_зс)=0 имело все корни с отрицательными вещественными частями, но корни этого уравнения в матричной алгебре называются собственными числами матрицы А_зс, следовательно, условие устойчивости для модели в пространстве состояний (МПС) имеет следующий вид:

замкнутая система будет устойчивой тогда и только тогда, когда все собственные числа матрицы А_зс имеют отрицательные вещественные части.

Управляемость и наблюдаемость объекта управления

Пусть задана модель в пространстве состояний объекта управления (7,9).

Объект называется полностью управляемым, если для него можно подобрать такое управляющее воздействие u(t), с помощью которого можно перевести этот объект из любого заданного начального состояния Z(t0) в любое заданное конечное состояние Z(tкон).

--------------------16-17 билет--------------------

Объект называется полностью наблюдаемым, если все компоненты вектора состояния Z(t) можно вычислить на основании информации о входном и выходном сигналах на интервале времени t <= τ <= T.

Доказаны следующие критерии управляемости и наблюдаемости объекта

Объект будет полностью управляемым тогда и только тогда, когда матрица управляемости

M_[nxn] = [B | AB | A²B | … | A^n-1B]

имеет полный ранг, т.е. rang M = n.

Объект будет полностью наблюдаемым тогда и только тогда, когда матрица наблюдаемости

N = [C^T | A^TC^T | A^{T^2} C^T | … | A^{T^(n-1)} C^T]

имеет полный ранг, т.е. rang N = n.

--------------------18 билет------------------------

Понятие о модальном регуляторе

Свойства САР, заданной моделью в пространстве состояний, зависят от собственных чисел матрицы Азс. Например, для устойчивости замкнутой системы требуется, чтобы собственные числа матрицы Азс имели отрицательные вещественные части.

При проектировании высококачественных систем управления и фильтров сигналов, обладающих определенными свойствами, возникает задача – подобрать обратную связь для заданного объекта так, чтобы все собственные числа матрицы Азс расположились в заранее заданных местах на комплексной плоскости, в частности, на окружности некоторого радиуса. Эта задача сводится к следующему. Для заданного объекта (A,B,C,D) требуется определить матрицу k[1xn] так, чтобы все собственные числа матрицы Азс имели бы заданные значения на комплексной плоскости

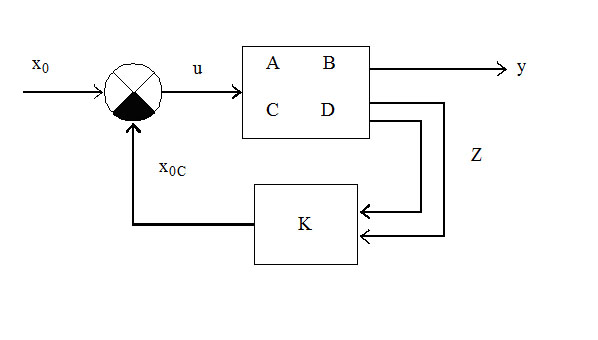
Рис.13. САР с модальным регулятором.

МПС замкнутой системы (рис. 13) получается следующим образом:

dz/dt = Az + Bu ; y = Cz + Du – модель объекта,

xос = k z – модель обратной связи ,

u = x0 – xос –модель устройства сравнения.

Отсюда получаем модель замкнутой системы:

dz/dt = Az + B(x0 – kz) = (A – Bk)z + Bx0 = Азс z+ Bx0,

где Азс = A[nxn] – B[nx1]k[1xn].

Характеристическое уравнение замкнутой системы будет иметь вид:

det(pE – A + Bk) = 0 (17).

Уравнение (17) является уравнением n-ной степени вида

cnpn+cn-1pn-1+….+c0=0 , где ci=fi(k1,…,kn).

Задача сводится к расчету значений k1, …, kn так, чтобы это уравнение имело заданные значения корней p1, …, pn. Доказана следующая теорема:

Задача определения матрицы k[1xn] имеет решение тогда и только тогда, когда объект (A,B,C,D) является полностью управляемым.

Обратная связь по вектору состояния z (рис. 13), обеспечивающая расположение собственных чисел матрицы Азс в заданных местах на комплексной плоскости, называется модальным регулятором.

Таким образом, задача синтеза модели регулятора имеет решение тогда и только тогда, когда объект является полностью управляемым.

--------------------19 билет------------------------

Практическая реализация модального регулятора требует наличия информации о значении всех компонентов вектора состояния z(t) в любой момент времени t, однако чаще всего невозможно (практически) иметь датчики для измерения всех компонентов вектора состояния. В этом случае модальный регулятор можно построить по схеме (рис.14):

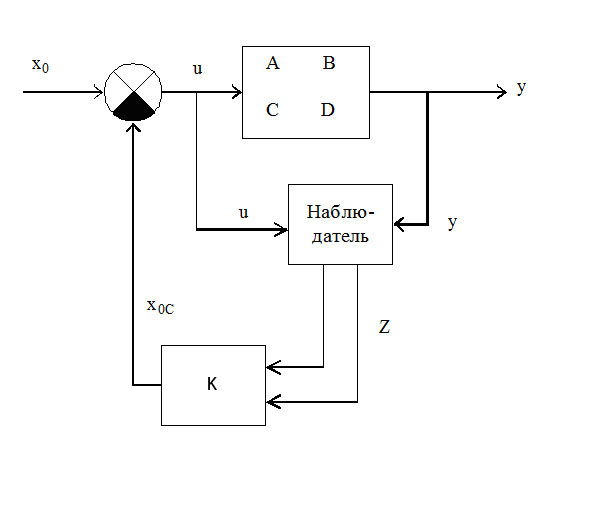
Рис.14. САР с наблюдателем и модальным регулятором.

В этой схеме имеется блок «наблюдатель», который выполняет расчет вектора состояний z на основании информации о сигналах y(t) и u(t). Это возможно, если объект (A,B,C,D) является полностью наблюдаемым. Наблюдатель и модальный регулятор в схеме (рис. 14) реализуются, как правило, в виде соответствующих программ на ЭВМ. Эта реализация возможна только тогда, когда объект является полностью управляемым и полностью наблюдаемым.

--------------------20 билет------------------------