- •Двойной интеграл
- •2. Двойной интеграл
- •4. Тройной интеграл
- •5. Тройной интеграл
- •6. Тройной интеграл
- •7. Замена переменных в тройном интеграле
- •9. Приложения тройного интеграла
- •10. Криволинейный интеграл первого рода
- •11. Вычисление криволинейного интеграла первого рода.
- •12. Криволинейный интеграл 2-го рода
- •18. Ряды.
- •19Ряды.Св-ва рядов
- •20. Необх. Признак сходимости
- •25. Знакочередующийся ряд.
- •26. Знакопеременный числовой ряд.
- •30. Разложение функции в степенной ряд. Формулы Тейлора и Маклорена.
Двойной интеграл
Опр: если сущ-ет
придел указанной суммы lim
∑ f(
f( )*∆
)*∆ при условии что кол-во кусочков разбиения
стремится к D,
не зависящий ни от способа разбиения
области D
на части, ни от выбора промежуточной
точки М, то он называется двойным
интегралом по области D
от функции f(x,y)
при условии что кол-во кусочков разбиения
стремится к D,
не зависящий ни от способа разбиения
области D
на части, ни от выбора промежуточной
точки М, то он называется двойным
интегралом по области D
от функции f(x,y)

D – область интегрирования
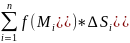 – интегральная
сумма для f(x,y)
– интегральная
сумма для f(x,y)
F(x,y)- подынтегральная фун-ия
F(x,y)ds – диф-ал элемента площади
Условия сущ-ия:
Необ.усл.
Ограниченность фун-ии в области D. Если интеграл существует, то ф-ия ограничена
Дост. Усл. Непрерывность фун-ии
Если фун-ия непрерывна, то интеграл сущ-ет.
Если придел сущ-ет, то он не зависит от разбиения обл. D на части, по этому разбивать на части мы будем прямыми параллельными осями координат
∆
= ∆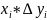
dS= dx*dy
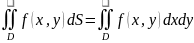
Геометрический смысл 2ого интеграла
Пусть обл. D ЄOxy. Пусть в этой обл. определена неотриц. Z=f(x,y)≥0 – обл. непрерывна
Vт=
 =
=

Двойной интеграл от неотриц. Функции = V тела огранич. Сверху поверхностью f(x,y) , а снизу обл. D
Масса пластинки

M
=

Свойства двойного интеграла
Пусть f(x,y), g(x,y) – инт-лы в обл D
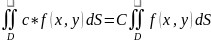
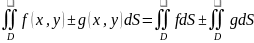
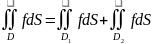 Если область D
разбита на 2 непересек. Области D1
и D2
внутренних
точек,
то D=
D1UD2
Если область D
разбита на 2 непересек. Области D1
и D2
внутренних
точек,
то D=
D1UD2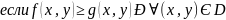 то
то

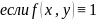
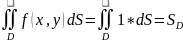
Если m≤ f(x,y) dS≤ M∀(x,y)Є D ,то m*

Если
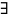
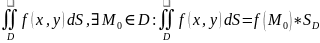
 -
среднее значение интеграла
-
среднее значение интеграла
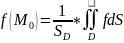
2. Двойной интеграл
Опр: если сущ-ет придел указанной суммы lim ∑ f( )*∆ при условии что кол-во кусочков разбиения стремится к D, не зависящий ни от способа разбиения области D на части, ни от выбора промежуточной точки М, то он называется двойным интегралом по области D от функции f(x,y)
D – область интегрирования
– интегральная сумма для f(x,y)
F(x,y)- подынтегральная фун-ия
F(x,y)ds – диф-ал элемента площади
Вычисление двойного интеграла в прямоуг. Сист. Координат
Vт=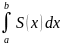
1)область правильная в напр. Оси у
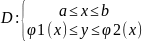
V=
;

V=
Второй интеграл сводится к повторному интегралу , внутр. Интеграл по dy, вычисляется при условии что х=const , потом вычисляется внешний интеграл по dx.
2) если область правильная в направлении оси ОХ

3. Замена переменных.
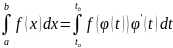
X=

dx=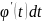
пусть z= f(x,y);
x=

y=

если
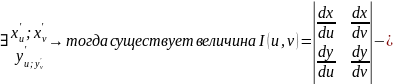 определитель
Якоби или Якобиана
определитель
Якоби или Якобиана
Теорема : Если сущ-ют частные производные и являются непрерывными, то имеет место формуле замены переменных в двойном интеграле.
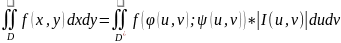 ;
;
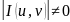
Область D та же область, но отличается она через другие уравнения ( в др. координатах)
Полярные координаты:
X
=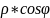
Y=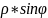
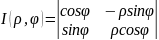 =
=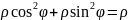
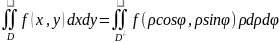
dxdy
4. Тройной интеграл
U=f(x,y,z)- Функция 3х переменных
TЄR3
lim – интегральная сумма д/функции 3х
переменных по области V
– интегральная сумма д/функции 3х
переменных по области V
Если существует предел интегральной суммы при условии, что он не зависит от разбиения на части и выбора промежутка, то он называется тройным интегралом по области от функции 3х переменных.
Если
этот предел не зависит от способа
разбиения, то область будем разбивать
плоскостью // координатным плоскостям,
и i-тый
кусок будет параллелепипед со сторонами
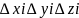
Vпаp=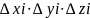
dv=dx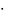 dy
dz
dy
dz
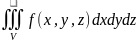
Условие существования – непирывность функции в области V
U=f(x,y,z)
2) масса тела
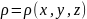
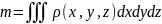
Задача.
найти массу тела,если его объемная
плотность в кажд точ числ равна ординате
этой точки. Тело огранич пов-ми:
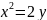 ,
y+z=1,
2y+z=2
,
y+z=1,
2y+z=2