
- •Модуль непрерывности. Равномерная непрерывность функции на множестве.
- •Равномерная непрерывность функции, непрерывной на отрезке
- •Производная. Определение, непрерывность функции, имеющей производную. Геометрический смысл производной.
- •Геометрический смысл производной.
- •Билет 4 Дифференциал функции. Определение. Геометрический смысл.
- •Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Арифметические свойства производной.
- •Производная сложной функции. Дифференциал сложной функции. Инвариантность формы первого дифференциала.
- •Производная обратной функции. Производные элементарных функций.
- •Возрастание (убывание) функции в точке. Необходимое условие, достаточное условие возрастания (убывания) функции в точке. Теорема Ферма.
- •Теорема Ролля. Геометрический и физический смысл.
- •Теорема Коши. Физический смысл.
- •Теорема Лагранжа. Геометрический и физический смысл. Формула конечных приращений.
- •Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
- •Условие постоянства функции на отрезке.
- •Достаточные условия экстремума.
- •Формула Тейлора для многочленов.
- •Формула Тейлора для дифференцируемых функций с остаточными членами в форме Пеано, Лагранжа, Коши. Единственность разложения.
- •Формула Тейлора для основных элементарных функций.
- •Билет 22 Выпуклость функции в точке. Достаточное условие.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Непрерывна в и . Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или , а если четное, то есть точка перегиба кривой.
- •Правило Лопиталя. Случай 0/0.
- •Раскрытие неопределенностей вида , , , , .
- •Асимптота. Виды асимптот. Уравнение наклонной асимптоты.
- •Первообрáзная. Неопределенный интеграл. Свойства.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям неопределенного интеграла.
- •Интегрирование простейших рациональных дробей
- •Теорема о разложении рациональной дроби на элементарные.
- •Интегрирование рациональных дробей.
- •Интегрирование тригонометрических выражений.
- •Первая подстановка Эйлера (Леонарда)
- •Интегрирование выражений вида .
- •Тригонометрические подстановки.
Интегрирование рациональных дробей.
Пусть
нужно найти неопределенный интеграл
![]() от рациональной действительной дроби.
Если степень многочлена P
k
не меньше степени многочлена Q
n
(
от рациональной действительной дроби.
Если степень многочлена P
k
не меньше степени многочлена Q
n
(![]() ),
то прежде всего разделим P
на Q
:
),
то прежде всего разделим P
на Q
:
![]()
Многочлен
R
интегрируется без труда, а
![]() – правильная действительная дробь. Все
трудности сводятся к интегрированию
правильной дроби, которую мы снова
обозначим через
– правильная действительная дробь. Все
трудности сводятся к интегрированию
правильной дроби, которую мы снова
обозначим через
![]() и
представим в виде:
и
представим в виде:
![]()
Тогда
пусть
![]() ,
,
![]()
1 случай.
Знаменатель содержит простые действительные корни, тогда его можно разложить на простейшие множители: (см.Теор.1)
![]() .
Тогда
.
Тогда
![]()
Приравнивая тождественно равные числители, получим:
![]()
Существуют
2 метода нахождения
![]() :
:
сравниваем коэффициенты при x с одинаковыми степенями; однако этот метод очень трудоемкий.
Т.к. равенства тождественны, можем взять
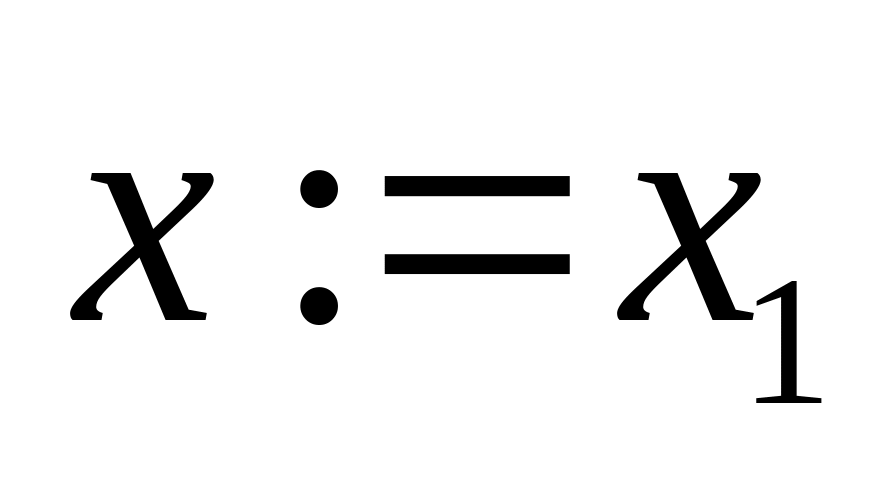 ,
тогда
,
тогда
 .
Так, подставляя поочередно
.
Так, подставляя поочередно
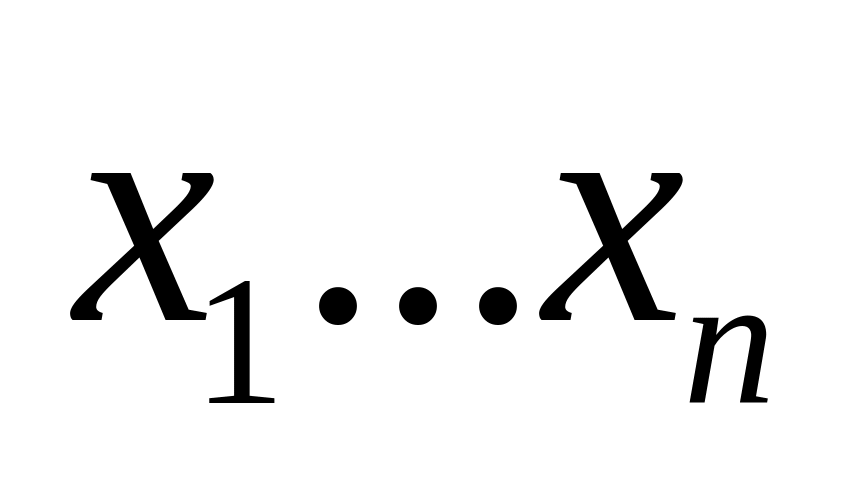 найдем все
найдем все
Т.о., мы получили сумму элементарных дробей, которые можем легко проинтегрировать.
Пример
![]()
2 случай.
Знаменатель содержит кратные корни, тогда его можно представить в виде:
![]() .
.
Пусть
существуют n
различных корней с кратностями
![]() ,
тогда
,
тогда
![]() - и делаем все
так же, как и в предыдущем примере.
- и делаем все
так же, как и в предыдущем примере.
Пример
![]()
3 случай.
Знаменатель содержит кратные корни и многочлены, имеющие комплексные корни;
![]() ,
где многочлены
,
где многочлены
![]() ,
,
![]() имеют комплексные корни.
имеют комплексные корни.
Тогда R(x) представим в виде:
![]()
Снова приводим к общему знаменателю и приравниваем числители.
Пример
![]()
4 случай
Знаменатель содержит кратные действительные и кратные комплексные корни;
![]()
Тогда R(x) представим в виде:
![]()
А дальше все делаем по старой схеме: методом неопределенных коэффициентов находим A, B...
Пример
![]()
Билет 33
Интегрирование тригонометрических выражений.
Пусть
![]()
![]() ,
где
,
где
![]() и
и
![]() - многочлены от u
и v.
- многочлены от u
и v.
1)
Если один из многочленов
,
четный по
![]() ,
а другой – нечетный по
,
то подстановка
,
а другой – нечетный по
,
то подстановка
![]() рационализирует интеграл.
рационализирует интеграл.
2)
Если один из многочленов
,
четный по
![]() ,
а другой – нечетный по u,
то подстановка
,
а другой – нечетный по u,
то подстановка
![]() рационализирует интеграл.
рационализирует интеграл.
3)
Если оба многочлена четные по u
и
,
то подстановка
![]() рационализирует интеграл.
рационализирует интеграл.
3’)
Выражения вида
![]() ,
где
,
где
![]() и
- четные. Они сходны с 3 случаем, где
и
- четные. Они сходны с 3 случаем, где
![]()
4) Универсальная подстановка.
Рационализация
![]() также достигается с помощью подстановки
также достигается с помощью подстановки
![]() ,
которая называется универсальной.
В самом деле,
,
которая называется универсальной.
В самом деле,
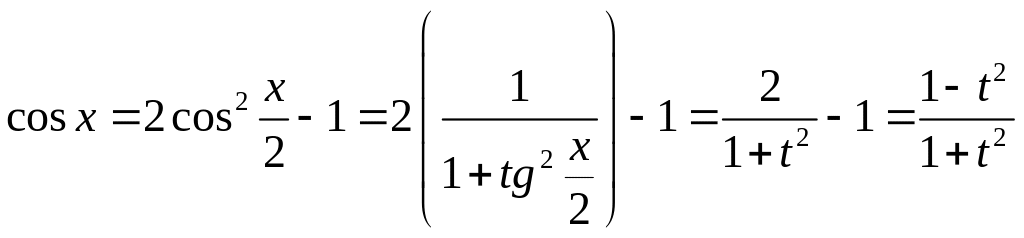 ;
;
 ;
;
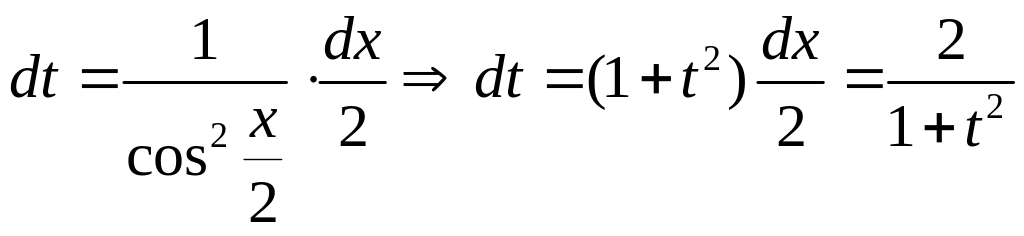
![]() .
.
5)
Выражения вида
![]() ;
;
![]() ;
;
![]() .
Они рационализируются с помощью перевода
в тригонометрические суммы.
.
Они рационализируются с помощью перевода
в тригонометрические суммы.
Билет 34
Первая подстановка Эйлера (Леонарда)
![]()
Пусть
многочлен
![]() имеет
вещественные корни.
имеет
вещественные корни.
Пусть
![]() - корни, тогда
- корни, тогда
![]() .
.
Рассмотрим
подстановку
![]()
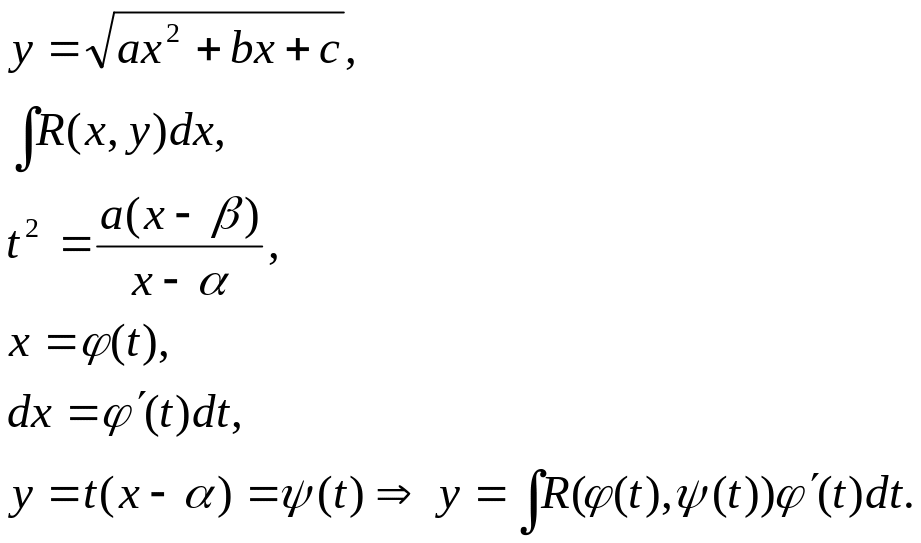
Вторая подстановка
Эйлера для
интегралов вида
![]() ,
где
,
где
![]() .
.
Корни
трехчлена ax2+bx+c комплéксные. Тогда надо
считать, что a>0, иначе трехчлен был бы
отрицателен для всех x. Делаем
подстановку![]() .Возводя
это равенство в квадрат и заменяя
.Возводя
это равенство в квадрат и заменяя
![]() его выражением, получим:
его выражением, получим:
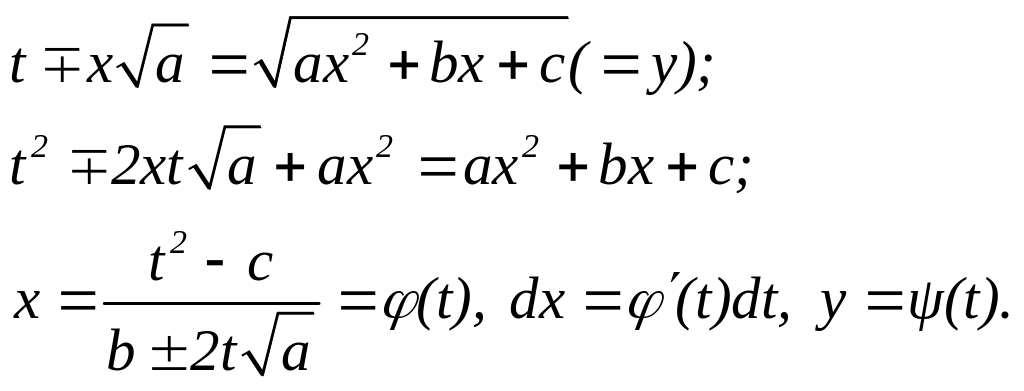
Где x, y и dx – некоторые рациональные функции от t. В конечном счете получаем:
![]() .
.
Билет 35
Интегрирование выражений вида .
Докажем,
что любой такой интеграл – берущийся
в элементарных функциях. Пусть![]() ,
т.к.
,
т.к.![]() .
Пусть m=НОК
.
Пусть m=НОК![]() ,
,![]() .
Сделаем замену:
.
Сделаем замену:![]() ,
тогда
,
тогда![]() ,
причем последнее выражение - рациональное,
т.к. m делится на любое
,
причем последнее выражение - рациональное,
т.к. m делится на любое
![]() .
.
Тогда
получим, что x=φ(t), dx=φ΄(t)dt, где φ(t) и φ΄(t)dt
– рациональные выражения, поэтому:
![]() - тоже рациональное выражение
- тоже рациональное выражение
Билет 36
