
- •2.Случайные события и их классификация.
- •3.Действие над событиями (объединение, пересечение, разность)
- •4.Основные правила и формулы комбинаторики.
- •5.Классическое определение вероятности.
- •7.Теоремы сложения вероятности.
- •8.Теорема умножения вероятности.
- •9.Формула полной вероятности.
- •10.Формула Байеса.
- •15.Функция распределения случайной величины и её свойства.
- •16.Дискретно распределённая случайная величина.
- •17.Непрерывно распределённая случайная величина.
- •18.Биномиальный закон распределения св.
- •26.Теорема Бернулли.
- •27.Предемет математической статистики.
- •28.Генеральная и выборочная совокупность.
- •29.Статиситическое распределение выборки.
- •30.Эмперическая функция распределения.
- •31. Графическое изображение статистического распределения
- •33.Точечное оценивание параметров распределения.
- •34.Интервальное оценивание параметров распределения.
- •35. Доверительный интервал и доверительная веротность.
- •36. Доверительные интервалы математического ожидания и для дисперсии нормально распределенной случайной величины.
- •37. Статис-ая гипотеза, статис-й критерий, ошибки первого и второго рода.
- •38. Критическая область, мощность критерия.
- •39. Схема проверки стат-ой гипотезы.
- •42.Критерий согласия пирсона.
- •43. Основные понятия корреляционного и регрессионного анализа.
- •44)Линейная корреляционная зависимость и прямые регрессии
- •45)Коэффициент линейной корреляции и его свойства
26.Теорема Бернулли.
Если
в каждой из п
независимых испытаниях вероятность р
появления события А
постоянно, то как угодно близка к единице
вероятность того, что отклонение
относительной частоты от вероятности
р
по абсолютной величине будет сколь
угодно малым, если число п
достаточно велико:
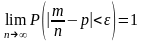
27.Предемет математической статистики.
Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдения массовых случайных явлений для выявления существующих закономерностей. Первая задача математической статистики – указать способы сбора и группировки статистических данных, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Второй задачей математической статистики является разработка методов анализа статистических данных в зависимости от целей исследования. К этой задаче относятся: оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и т.п.
Третья задача - проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
28.Генеральная и выборочная совокупность.
Генеральная совокупность – это все исходы случайного испытания, вся совокупность значений случайной величины Х или всевозможные наблюдения интересующего нас показателя. Выборочная совокупность – часть объектов генеральной совокупности, используемая для исследования.
29.Статиситическое распределение выборки.
Значение признака xi |
X1 |
X2 |
… |
Xк |
Частота mi |
m1 |
m2 |
… |
mк |
30.Эмперическая функция распределения.
Эмперич.
ф-ция распределения – ф-ция определяющая
зависимость между количественными
признаками и накопленными частотами.
F(x)=ωx.
использовать
эмпирическую функцию
![]() в качестве приближения теоретической
функции
в качестве приближения теоретической
функции
![]() - функции распределения генеральной
совокупности.
- функции распределения генеральной
совокупности.
Свойства эмпирических функций распределения
1)
![]()
2) - неубывающая
3)
![]() - наименьших вариантов;
- наименьших вариантов;
![]() - наибольших вариантов.
- наибольших вариантов.
31. Графическое изображение статистического распределения
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Полигоном
частот
называют ломаную линию, отрезки которой
соединяют точки
![]() .
Для построения полигона частот на оси
абсцисс откладывают варианты
.
Для построения полигона частот на оси
абсцисс откладывают варианты
![]() ,
а на оси ординат – соответствующие им
частоты
,
а на оси ординат – соответствующие им
частоты
![]() и соединяют точки
и соединяют точки
![]() отрезками
прямых.
отрезками
прямых.
Гистограммой
частот называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которой
служат частичные интервалы длиною h,
а высоты равны отношению
![]() .
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го
прямоугольника равна
.
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го
прямоугольника равна
![]() – сумме частот вариант i–о
интервала, поэтому площадь гистограммы
частот равна сумме всех частот, т.е.
объему выборки.
– сумме частот вариант i–о
интервала, поэтому площадь гистограммы
частот равна сумме всех частот, т.е.
объему выборки.
Выборочной
дисперсией
![]() называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения
называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения
![]() .
Если все значения
.
Если все значения
![]() признака
выборки объема n
различны, то:
признака
выборки объема n
различны, то:
![]() .
.
32
Вариационный
ряд
Если значения признака
![]() имеют
частоты
имеют
частоты
![]() соответственно, причем
соответственно, причем
![]() ,
то:
,
то:
![]() .
.
![]()
ОПР: коэф-ом вариации наз-ся процентное отношение сред. квадрат-го отклон-я к сред арифм-й
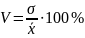
Медианой называется значение варианты находящееся в середины вариационного ряда.
