20. Численное интегрирование и дифференцирование.

Численное интегрирование.

В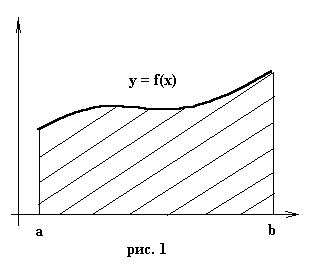 прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла

О н может выражать площадь, объем, работу переменной силы и т.д.

Если функция f(x) непрерывна на отрезке [a;b] и ее можно выразить через известные функции, то для вычисления интеграла (1) можно воспользоваться формулой Ньютона- Лейбница:

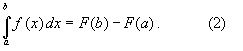
Однако в действительности очень часто получить решение (1) с помощью формулы (2) или других аналитических методов невозможно.

Примером может служить широко применяемый для исследования процессов теплообмена и диффузии, в статистической физике и теории вероятностей интеграл:

з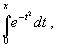 начение, которого не может быть выражено в виде конечной комбинации элементарных функций.

Помимо этого вычисления интеграла (1) в аналитической форме могут быть длительным и трудоемким процессом, приводящим к приближенному результату, или не дающими такового совсем.

На практике помимо аналитических методов широко применяются специальные численные методы. Наиболее широко применяются квадратурные формулы вида:

- некоторые т., ∊[a; b] – узлы квадратной ф-лы;

А_i – числовые коэф., называемые весами квадратной формулы.

В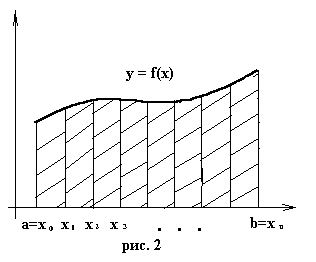 ыведем простейшие квадратурные формулы, исходя из геометрических соображений. Известно, что интеграл (1) - площадь криволинейной трапеции, ограниченная сверху функцией f(x) (рис.1).

Разобьем отрезок [a;b] на элементарные отрезки [x_i-1,x_i ] точками

При этом интеграл будет представлять сумму своих составляющих.

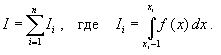
Будем считать шаг h=x_i-x _i-1 постоянным и введем обозначения f_i = f (x_i), f_i-1/2 = f (x_i-1/2),

где x_i-1/2 = (x_i-1/2 + x_i) / 2 - середина элементарного отрезка.

Формула прямоугольников. Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоуголника с основанием [xi-1, xi] и высотой fi-1/2.

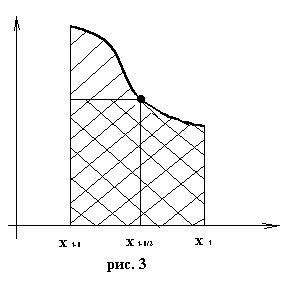
Таким способом мы переходим к элементарной квадратурной формуле прямоугольников

П роизведя такую замену для всех элементарных криволинейных трапеций (рис. 2), получим составную квадратурную формулу прямоугольников:

В результате получаем замену площади исходной криволинейной трапеции площадью ступенчатой фигуры. Помимо формулы (4) на практике используют формулы левых и правых прямоугльников:

Формула трапеций. Соединим Ni-1 (xi-1, f i-1) и Ni(xi, fi) на графике функции y = f(x).

В результате получится трапеция (рис.4). Заменим приближенно площадь элементарной криволинейной трапеции площадью построенной фигуры. Получим элементарную квадратурную формулу трапеции:

Составная квадратурная формула трапеции будет представлять собой:

Эта формула соответствует замене исходной фигуры (см. рис.1) ломанной линией, проходящей через точки N0, ... , Nn.

Формула Симпсона. Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки Ni-1, Ni-1/2,, Ni, то получим приближенное равенство:

г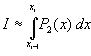 де P2 (x) - интерполяционный многочлен второй степени с узлами xi-1, xi-1/2, xi.

Нетрудно убедиться, что верна формула:

Интегрирование этой формулы приводит к равенству:

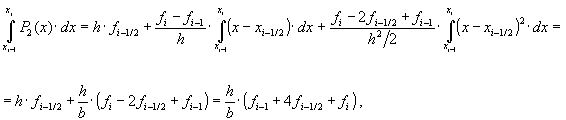
которое представляет собой элементарную формулу Симпсона. От нее легко можно перейти к составной квадратурной формуле Симпсона:

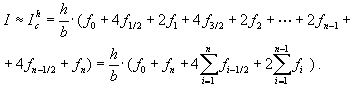
Численное дифференцирование.

Во многих задачах решение включает необходимость вычисления производных. Если функциональная зависимость f(x) имеет простой вид, то в вычислительных алгоритмах можно использовать явный вид производной f`(x) для определения ее числовых значений. Однако, в реальных ситуациях, функция f(x) может быть представлена математической моделью или конечным множеством точек (x_i; f_i(x)). В этом случае отсутствует возможность пользоваться аналитическим выражением производной. Вспомним определение производной:

можно использовать приближенное числовое значение:

- производная слева

- справа

Вторую производную в точке x_i можно рассчитать по этой же формуле:

и так далее.

Данные формулы дают достаточно высокую точность при задании h→0. отдельный случай представ. Случай когда функция f(x) задана таблицей. Здесь отсутствует возможность определения ∆x. Выходом в данной ситуации может быть использование интерполяционных методов. Покажем использование алгоритма Лагрнажа L2,i(x), проходящего по точкам xi-1,xi,xi+1.

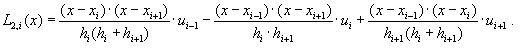
Значение производной f'(x) будет приближенно совпадать с L2,i(x).