1. Математическая постановка задач оптимизации. Критерии оптимизации. Виды ограничений. Классификация задач: задачи безусловной и условной оптимизации, одномерной и многомерной оптимизации, задачи нелинейного, линейного, целочисленного программирования, задачи оптимизации на сетях.

Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например: - количество продукции - "расход сырья" – кол-во продукции - "качество продукции" Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.

Постановка задачи

Пусть функция f(x) - унимодальная, по крайней мере, на отрезке [a,b] и известны ее значения на концах этого отрезка. Т.е. минимум локализован и необходимо определить его как можно точнее, с наименьшим возможным интервалом неопределенности, но при этом возможно выполнить только n вычислений функции? Как следует выбрать n точек xk, k=1,..,N вычисления функции на отрезке [a,b], чтобы как можно точнее определить минимум?

Виды ограничений

Несмотря на то, что прикладные задачи относятся к совершенно разным областям, они имеют общую форму. Все эти задачи можно классифицировать как задачи min-ции вещественнозначной функции f(x) N-мерного векторного аргумента x=(x₁, x₂,..., x_n), компоненты которого удовлетворяют системе уравнений h_k(x)=0, набору неравенств g_i(x) 0, а также ограничены сверху и снизу, т.е. x_i^(u) x_i x_i^(l). В последующем изложении функцию f(x) будем называть целевой функцией, уравнения h_k(x) =0 - ограничениями в виде равенств, а неравенства g_i(x) 0 - ограничениями в виде неравенств. При этом предполагается, что все фигурирующие в задаче функции являются вещественнозначными, а число ограничений конечно.

Классификация задач

Задачи оптимизации можно классифицировать в соответствии с видом функций f, hk, gi и размерностью вектора x. Задачи без ограничений, в которых x представляет собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но вместе с тем весьма важный подкласс оптимизационных задач. Задачи условной оптимизации, в которых функции hk, и gi являются линейными, носят название задач с линейными ограничениями.

В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи, которые содержат только линейные функции вектора непрерывных переменных x, называются задачами линейного программирования; в задачах целочисленного программирования компоненты вектора x должны принимать только целые значения.

С точки зрения методологии изложения методов минимизации функций целесообразно выделить такие задачи.

1.Безусловная минимизация функций:

В этом случае область задания функции Q - все n-мерное евклидово пространство, т. е. на переменные функции ограничений не накладывается вообще. Очевидно, что минимум функции (если он существует) всегда находится внутри ее области задания, поскольку последняя просто не имеет границ.

2.Минимизация функций при ограничениях в виде равенств:

у(х)

W : fi(х)=0 (i=1, ... , m; m<n)

Область задания W функции- бесконечное множество решений системы уравнений, представляющее собой p-мерную поверхность в n-мерном пространстве. Поскольку любая точка х W лежит на поверхности fi (х) == 0 (i = 1, ... , m) и, следовательно, является граничной, то и минимум (в случае его существования) также лежит на границе области W.

3.Минимизация функций, заданных на гиперпараллелепипеде:

у(х)

W : fi(х) =0 (i=m+1,... , m+k)

fi(х) = 0 (i=1, ..., m).

Здесь минимум функции может находиться внутри области и на ее границах

4.Минимизация функций при ограничениях в виде неравенств.

у(х)

W : fi(х)  0 (i=1, :. , k)

х 0

Минимум может находиться внутри области W и на ее границе.

Задачи 1, 2 обычно относят к классическим задачам оптимизации; 3, 4 называют задачами математического программирования. Легко видеть, что задачи 1-3-частный вырожденный случай задачи 4.

2. Одномерная оптимизация. Необходимые и достаточные условия оптимальности. Принцип сужения интервала неопределенности для унимодальных функций.

Несмотря на то, что безусловная оптимизация функции одной переменной наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных интерактивных процедур многопараметрической оптимизации.

Своеобразным индикатором важности методов оптимизации функции одной переменной является огромное множество реализованных алгоритмов, которые условно можно сгруппировать следующим образом:

• методы исключения интервалов:

• метод половинного деления;

• метод "золотого" сечения;

• метод Фибоначчи;

• методы полиномиальной аппроксимации;

• методы с использованием производных.

Метод уменьшения интервала

Методы поиска, которые позволяют определить оптимум функции 1-ой переменной путем уменьшения интервала поиска, носят название методов исключения интервалов. Все методы одномерной оптимизации основаны на предположении, что исследуемая целевая функция в допустимой области по крайней мере обладает свойством унимодальности, так как для унимодальной функции W(x) сравнение значений W(t) в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подинтервалов точки оптимума отсутствуют.

П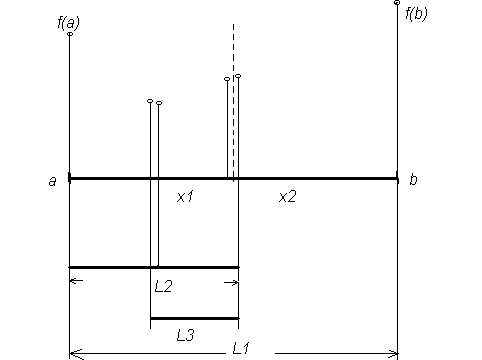 равило исключения интервалов. Пусть W(x) унимодальна на отрезке [a,b], а ее минимум достигается в точке x*. Рассмотрим x₁ и x₂, расположенные a<x₁<x₂<b.

1. Если W(x₁)>W(x₂), то точка минимума W(x) не лежит в интервале (a,x₁), т.е. x*Є О(x₁,b).

2. Если W(x₁)<W(x₂), то точка минимума W(x) не лежит в интервале (x₂,b), т.е. x*Є (a,x₂). Это правило позволяет реализовать процедуру поиска путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается тогда, когда оставшийся подинтервал уменьшается до достаточно малых размеров. Главное достоинство поисковых методов - основаны на вычислении только значений функции и, следовательно, не требуют выполнения условия дифференцируемости и записи в аналитическом виде. Последнее свойство особенно ценно при имитационном моделировании. Процесс применения методов поиска на основе исключения интервалов включает два этапа:

1.этап установления границ интервала;

2.этап уменьшения интервала.

3. Одномерная оптимизация. Постановка задачи. Метод половинного деления. Оценка погрешности.

Постановка задачи.

Пусть функция f(x) - унимодальная, по крайней мере, на отрезке [a,b] и известны ее значения на концах этого отрезка. Т.е. минимум локализован и необходимо определить его как можно точнее, с наименьшим возможным интервалом неопределенности, но при этом возможно выполнить только n вычислений функции? Как следует выбрать n точек x_k, k=1,..,N вычисления функции на отрезке [a,b], чтобы как можно точнее определить минимум

Метод половинного деления

Найти W(x) на отрезке [a,b].

Шаг 1. x_m=(a+b)/2; L=b-a; вычислить W(x_m).

Шаг 2. x₁=a+L/4; x₂=b-L/4; вычислить W(x₁) и W(x₂).

Шаг 3.

• Если W(x₁)<W(x_m), то исключить (x_m,b], т.е. b=x_m, x_m=x₁. Перейти к шагу 5.

• Если W(x₁)> W(x_m), то перейти к шагу 4.

Шаг 4.

• Если W(x₂)<W(x_m), то исключить [a,x_m), т.е. a=x_m, x_m=x₂. Перейти к шагу 5.

• Если W(x₂)>W(x_m), то исключить [a,x₁) и (x₂,b], т.е. a=x₁, b=x₂. Перейти к шагу 5.

Шаг 5. L=b-a. Если | L| <e , то закончить поиск. В противном случае вернуться к шагу 2.

Как видно из алгоритма, из каждых трех значений целевой функции W, вычисленных в интервале поиска, в дальнейшем используется только два, а третья не дает дополнительной информации и в дальнейшем не используется.

Оценка погрешности